[译]背景:着色的物理和数学(3)
[译]背景:着色的物理和数学(3)
(译者注:本文是翻译的Naty Hoffman的《Background: Physics and Math of Shading》。我希望通过翻译此文,彻底理解PBR的原理。某些我实在不知道如何恰当翻译的地方,就把英文原文也放上了。)
下表面反射(Diffuse项)
文献中有几种下表面局部反射的模型,Lambertian模型[49]是最简单的,也是应用最广泛的。Lambertian的BRDF实际上是个常量;著名的cos或(nl)因子是反射率方程的一部分,不是BRDF的一部分(如我们在Equation 1所见)。Lambertian的BRDF值为:
这里,cdiff是diffuse反射的部分。像F0一样,它是个RGB值,范围为[0, 1],对应着大多数人认为的那个“表面颜色”。这个参数一般被称为diffuse颜色。
其他的模型尝试引入Lambertian模型没有的现象,例如specular和diffuse项在掠射角下的能量分配问题。diffuse项对下表面反射建模,所以只能利用没有被表面反射出去的入射能量。某种意义上,specular项指着入射光能量大喊“归我了”,然后diffuse项只能用“剩下的”。由于菲涅耳效果使得specular项在掠射角增大,结果就是diffuse项在这些角度上必须减小。有很多研究想搞定这个问题,简单的有(用(1-菲涅耳因子)乘以diffuse项(用Schlick Fresnel项的一部分作为插值因子,使得BRDF有了在diffuse和specular项之间线性插值的形式)),更复杂更精确的也有[2, 3, 41, 65]。
(译者注:记住Lambertian模型就好,其他的暂时不重要)
其他的diffuse模型尝试计入表面粗糙度的影响。很重要的一点是,要理解数量级在这个现象中的角色。如我们所见,下表面散射使得光在表面之下传输了一段距离,之后才被重新放出(反射出去)。小于这段距离的表面不规则性质都对下表面反射没有影响,因为任何反射出来的光都已经进入过大于这个不规则地带的表面了。但是,某些表面的粗糙范围比散射距离更大,这会展示出与Lambertian模型明显不同的外观。多种模型已经被开发出来解决这个问题[32, 60]。很多人误以为这些模型是用于渲染特别粗糙的表面的,其实并不是——关键的判据不是粗糙程度,而是表面细节上相对与下表面散射距离的粗糙的尺寸。
其它项
前文提过,在用diffuse项(multiple-bounce的下表面散射)和微平面项(single-bounce的表面反射)建模的现象中,有两种类型的反射现象被忽略了。
一个是下表面单次散射,即光的一部分被拆分进入表面,经历一次散射,然后就被折射出表面外。这一现象同时展示了diffuse和specular的特征;它高度依赖角度,它还会受表面下的介质的属性影响。
另一个现象是multiple-bounce的表面反射,即光在离开表面前被表面上多个点反射过。如前文所述,微平面模型忽略了多次表面反射——它实际上假设所有被遮蔽的光线都损失掉了,因此它比真实世界多了一些能量损失。
引入额外的BRDF项以涵盖这两种现象也许是可行的,但是目前还没有关于它们的已发表的良好的模型。注意,这些现象也会影响(区分下表面反射和表面反射)的方法(例如偏振测定polarimetry)。例如,single-bounce的下表面反射大量保留了偏振(译者注:不懂),所以用偏振测定法测量的“表面反射”也会包含这一现象的部分贡献。
实现产品级的物理着色模型
之前的章节中,我们看到了典型的用于描述表面反射的数学模型。本节我们将简要讨论这样的模型是如何运用到电影和游戏产品中的。
为实现一个着色模型,需要联系一个光照模型。接下来的章节,我们将简述最常见类型的光照模型,以及如何将它们与BRDF联系起来。
一般光照
在最一般的情况下,BRDF必须被集成到所有方向的入射光上。这包括天空光和场景中其他物体反射的光。为解决这问题,全局光照算法(例如蒙特卡罗光线追踪)是必需的。这些算法的详情超出本文的范围,但是在很多参考资料[17, 24, 31, 42, 43]中可以找到详细介绍。
基于图像的光照
基于图像的光照(Image-based Lighting)一般将光照信息存储到环境贴图中。环境贴图可以很容易地表示光滑(镜子那样的)物体的反射特征。菲涅耳反射率用Equation 5建模(用观察者向量代替光向量(到镜像法线的角度不变,所以代替前后是一样的))。困难点在于表面法线背向观察者方向时(可能由插值的法线或凹凸映射引起),这会同时影响反射方向和菲涅耳反射率(尽管错误的反射方向几乎不会被注意到)。如前文所述,裁剪为0或用绝对值都可以避免观察者与法线的点积为负数;在此特殊情形下,更倾向于采用绝对值。不像裁剪为0,取绝对值会把(掠射角相关的菲涅耳值)限制到(一个很窄的像素带上),这样看起来比较真实。
环境贴图也可以被用与任意BRDF函数,但可能需要多次采样才能避免噪音,得到精确的结果。重要性采样[14]有助于将采样量保持在可控的范围内(至少对电影渲染时)。环境贴图前置过滤[39, 40]是另一个产品级的有效方案:它自己(施展单独的前置过滤采样——游戏中常用,电影中不常用)或联合重要性采样[13, 14]。虽然单独的前置过滤采样原则上是反射率公式的粗放近似, 但只要好好用它还是很高效的。It is important to ensure that the prefiltering process accounts for the environment map representation used [36] as well as the shape and size of the NDF lobe [38, 46, 50]. 然后,读取前置过滤采样的时候,要乘以一个近似反射率积分的因子。这可以看作将积分分解为两个因子相乘:前置过滤环境贴图查询因子和用于shader的因子[22, 28, 38, 50]。
理论上,一个环境贴图只能用于一个物体的反射。这个环境贴图要要描述从一个靠近物体的点观察到的场景(不包含此物体本身)的样子,物体本身要是凸的,并远离周围场景。实际中很多这些假设都不成立。Non-convex objects should self-occlude the environment——this can be ignored (common in games), approximated with some simple occlusion term such as AO [29], or modeled more accurately by tracing rays against some representation of the object [22, 57, 67]. Reflected objects may also be close enough to have noticeable parallax over different surface points——especially common when the reflecting object is large. Finally, the environment map may be sampled from a different location in the scene, or even from a different scene entirely. It turns out that in many cases, the human eye is largely insensitive to the errors caused by parallax or use of environment maps away from their sample location. As long as the overall color and intensity is correct, the shapes being reflected can often be completely wrong without the viewer noticing. It is fairly straightforward to match the overall color and intensity of an environment map to local scene lighting [50], making environment maps an effective tool in many situations. Instances where incorrect reflections are noticeable (e.g. shiny floors, the player's car in a racing game, a shiny metallic hero character in a movie) can often be addressed by warping the reflections as a corrective step [47, 48, 67].
面积光源
太阳和台灯这样的光源,既有强度又有面积。理论上,它们可以用环境贴图中的一批HDR纹素处理,但是单独对待它们有更多的好处。(根据面积光源)计算阴影比(根据基于图像的光照)简单,视差可以被处理得更准确,艺术家也更容易调整光源的位置、亮度和尺寸,而不需要编辑基于图像的光照表示。
用面积光源对任意BRDF着色也比基于图像光照容易。多重重要性采样[72]可以大幅减少噪声[54](这一技术也可以用于基于图像的光照,但是对面积光源特别有效)。实时近似方案也有[22, 38],且越来越受欢迎。
精确光源
在游戏中(电影中也有),经常用精确光源近似模拟面积光源。经典的计算机图形学的点光源、平行光、聚光灯(也有更复杂一点的[5])都是精确光源。它们是无限小,无限亮的,所以不是现实世界可能存在的。但是它们很多时候能给出合理的结果,计算起来也很方便。
精确光源照射到表面点上的效果由2个量决定:光的颜色clight和光的方向lc。不同类型的精确光源,这些量在场景中可能是常量(平行光),也可能是变量(点光源随着距离衰减,其方向由物体和光源共同决定)。为便于可视化,clight一般被定义为在理想表面(100%的Lambertian表面,法线与光的方向lc平行)上的反射的辐射率。与其他颜色量类似,clight是个RGB值,但其值没有边界。
我们稍后将看到,精确光源最大的优势是极大地简化了辐射率方程(Equation 1)。我们从(一个表面点被一个单独的很小的面积光源照射)开始。光源被包裹进一个椎体里,角半径为ε,朝向lc,所以这个椎体外没有任何入射光:
我们根据clight的定义来测量面积光源在给定表面点上的光照。换句话说,clight等于表面点将会反射的辐射率(当材质是100%的白色Lambertian且其法线等于lc):
这就是将Equation 1和7的cdiff指定为1、n指定为lc。现在我们将ε设置为0,使得cligh为常量。由于我们将ε(lc和l之间的最大角度)设置为0,我们可以认定(lc·l)=1。此时得到了:
简单安排一下,将积分隔离出来:
现在我们要把我们的小小面积光源放到通用的BRDF函数中,看一下在ε逼近0时它的行为:
注意,在Equation 12中,通过提取f(lc, v)和(n·lc), 我们实际上交换了求极限和积分的顺序。只要BRDF函数f()表现正常(实际中用的所有BRDF肯定都是),这个交换就是有意义的。用Equation 11代替Equation 12的右边部分,我们就得到了最终的精确光源公式:
与原始的反射率公式相比,我们用单值的BRDF代替了积分,这在计算上很廉价。游戏中,经常将(点积裁切到0)作为跳过背面光贡献的简便方法。
上文提过,在平行光(例如太阳)情况下,lc和clight在整个场景中都是常量。对于其他类型的精确光源(点光源和聚光灯),这两个数值会变化。现实中,clight会随着距离平方的倒数的速度衰减,但在实践中常常使用其他衰减函数(为了性能(在有限距离内衰减为0就可以避免远距离物体的光照计算)或艺术效果)。
如果多个精确光源在照射表面,那么就将Equation 13多次计算,将结果相加。精确光源很少单独使用,因为缺失(从其他方向的光照)很明显,特别是高度specular的表面。,因此,精确光源经常和某种环境光或基于图像的光联合使用。后者我们讨论过了,前者将在下一节讨论。
环境光
这里我们将环境光定义为某种低频光照的表达,简单时是在所有方向上都相同的颜色和强度,复杂时是球面调和函数(SH)。这种光照类型常常放入BRDF的diffuse项,高频的、基于图像的光照则放入specular项。但是,把环境光放入specular项也是可能的。大多数这方面的已发表的方法都是从游戏工业引发的[11, 27, 64]。
建设一个基于物理的着色模型
本节,我们将探讨从零开始建设一个模型。关于将非物理模型转换为基于物理的模型的讨论,请参考我们的SIGGRAPH 2010展示[35]。
当要根据上文讨论的原则来建设一个基于物理的模型时,需要做出几个选择。需要选择一个diffuse模型,用于微平面specular模型的D()(法线分布函数)和G()(几何函数)也要选择。本节剩下的部分将关注这两个specular函数。
对D()和G()函数的选择,在某种程度上是相互独立的(对“某种程度”的解释可参考“选择几何函数”一节)。大多数论文给出的心微平面BRDF模型都可以被理解为是在引入一个新的D()和/或G()函数。
选择一个法线分布函数
最常见的NDF是各向同性的——它们关于由微平面表面法线n定义的轴是旋转对称的。这意味着NDF可以被定义为一个变量(m(微观几何体的法线)和n之间的角度)的函数。在shader中,最方便处理的是cos值,因为可以用点积来计算。因此,各向同性的NDF函数一般被写成n•m的函数。NDF相关的文献中已经给出了很多这样的函数,但是,它们必须全都被恰当地标准化之后才能用于微平面的BRDF。少数各向异性的NDF函数也被用于电影和游戏产业了,但由于篇幅的原因我们就仅限在各向同性的NDF里讨论了。
任何微观几何体分布函数都需要满足这样的要求:从任何角度看,可见的微观几何体面积加起来等于可见的微表面面积。跟准确地说,微观几何体的带符号投影面积的和要等于微观表面的带符号投影面积;这必须对所有观察角度都为真[73]。数学上,这意味着函数对任意的v必须满足下述公式:
注意,积分包含了整个球体,不是半球,cos因子没有被裁切——背面表面有负数的贡献。这个公式对所有微表面有效,不只是对高度领域。特别的,当v=n:
对BRDF的求值,追求的是NDF越容易计算越好,特别是在游戏和其他实时渲染应用程序中。对于光线追踪,每次采样都无比重要。
我们这里评审的所有微观几何体法线分布函数都被设计为仅用于计算前向的微观几何体的法线(即n•m≥0——这可以被理解为在高度领域建模,绝不会出现微观几何体法线与微表面法线夹角超过90°)。
这些函数不是用来对负值的n•m求解的,如果用了,就会出现意想不到的结果。在强制实施前向光照和观察方向的渲染器中,这不是问题,因为半向量(NDF的计算目标)也会前向。另外,法线插值和凹凸映射可能导致背向的观察向量,进而导致背向的半向量。这一般通过将n•m裁剪为0或(如果是在分母上,为避免除以零)一个很小的正数来解决。
Phong着色公式[61]是计算机图形文献中最早(也绝对是最有影响力的)提出的着色公式。
几年后它被Blinn[7]修改 为更适合微平面结构的BRDF(这一修改被通常被称为Blinn-Phong的BRDF,但是我们将简单地称它的NDF为“Phong NDF”)。尽管Blinn没有声明标准化因子,它也很容易计算:
指数αp是Phong NDF的“粗糙度”参数,高数值表示光滑平面,低数值表示粗糙平面。对于非常光滑的表面,此参数可以是任意大(完美的镜子会要求αp=∞)。如果设置αp为0,就会实现一个最大限度随机的表面(均匀的NDF)。αp参数不便于艺术家操作或绘画,因为它的影响非常不均匀。在αp很小的时候,很小的改变就会引起很大的视觉变化,但是大的αp值在变化很大后都不怎么影响视觉效果。因此,常用方法是让艺术家操作一个通过非线性方式继承了αp的“中间值”。例如,αp=ms,其中s是艺术家来操作的一个介于0和1之间的数值,m是一个给定的游戏或show中αp的上限。当BRDF的内部参数不便于直接用于生产应用时,这样的“中间函数”相当有用。Figure 30 shows Phong distribution curves for cosine powers evenly spaced according to a logarithmic scale.
在Blinn吸收了Phong着色函数并融入微平面NDF的论文[7]中,他还提出了2个其他的NDF。其中一个继承自Torrance-Sparrow的BRDF[70]。比较Torrance-Sparrow的BRDF和Phong,会发现它花费的计算代价高得多,取得的效果却很相似(详见随本讲义的数学笔记),所以这是死路一条。后来Cook和Torrance[15, 16]提出用一个新的NDF代替它,即Beckmann分布。正确地标准化之后,Beckmann分布有如下的形式:
Beckmann分布在某些方面和Phong分布很相似,但是其他方面有根本不同。根据关系式αp=2αb-2 - 2[73],可以找到这两个参数的相同的值,他们对相对光滑的表面(αb<0.5左右——更高的αb对应更粗糙的表面,这与αp相反)的反应很接近,如Figure 31左侧所示。对更光滑(αb<0.1)的表面,就接近得完美了。
鉴于Beckmann的表现与Phong相似,计算代价却更高,看起来它也是条死路。但是,它们参数的不同导致了其结果的根本性区别。参数αb等于微观几何体表面斜率的平方根。所以增加αb意味着增加微观几何体的平均斜率,这比“粗糙度”的“增加随机性”(通过减小αp)更加不同。Phong分布有个“最大粗糙度”参数值(αp=0,对应均匀的分布,其微观几何体的法线朝向半球上各个方向的概率都相同),对应的参数值(αb=1)对Beckmann却没有特殊的含义——它仅仅是表示微观几何体斜率的平方根为1,即45°。对于αb的中庸的值,我们可以看到Beckmann在分布的中间出现一个“下沉”,而不是Phong的水平直线(见Figure 31右侧)。当αb增长超过1后你会得到“超级粗糙”的表面,其微观几何体斜率的平方根很大——这比均匀分布的随机性弱,但在平坦方面更“粗糙”。观察曲线(Figure 32),我们可以看到随着粗糙度增加,分布中的“下沉”在90°变成了“反向高峰“(实际上是ring)。
这样“超级粗糙”的分布,对于建模现实世界的表面,有用吗?可能吧,由许多尖锐的纤维组成的表面可能会有这样的分布,绒状的微观结构在某种程度上与此分布也类似[1, 75]——其他材质也是可能的。无论如何,了解一些Beckmann分布在高值αb的行为还是很好的,不然,它只是一个Phong NDF的昂贵版本。
Blinn的论文[7]中提到的最后一个NDF(也是Blinn推荐使用的)来自Trowbridge和Reitz[71]。Blinn也没用为Trowbridge-Reitz NDF标明一个标准化因子,但是后来有篇论文[73]——称其为“GGX分布”——却给出了正确的因子。由于GGX分母的形式稍微复杂点(但是等价),我们使用的是原始版,其形式如下:
Figure 33展示了在参数αtr上的表现。增加参数值,表面就比较粗糙,这与Beckmann相似。Trowbridge-Reitz可以建模出一个均匀的分布(像Phong一样),也可以建模出一个“超级粗糙”的表面(像Beckmann一样)。
当比较Trowbridge-Reitz分布和Phong分布时(Figure 34),很明显,两种分布的图形有根本性区别。在参数空间上,Trowbridge-Reitz一致地表现出比Phong更窄的峰值(对于在高光中心给出相同值的参数值),围绕峰值的“尾巴”也更长。
Burley[10]提出了Trowbridge-Reitz的一个简单的“中间函数”:αtr=s2,其中s艺术家操作的值,范围为0-1。
着色模型需要在对真实世界建模时有良好的性能。数位研究者[20, 53, 55]已经发表了测量过的BRDF数据[18, 19, 56],其他人用这些数据(或者他们自己的测量数据)与多种着色模型比较过[10, 52, 76]。这些比较倾向于展示出许多材质没有被任何现有模型良好地建模了。最近,更多的研究用于开发专门为可测量的表面进行建模的模型[4, 10, 51]。我们用三个最近发表的这方面的工作作为我们对NDF的总览的结尾。
(译者注:这三种模型离我很远,暂时不翻译也不妨碍我目前的学习,所以就省略了。)
列出所有这些NDF之后,问题是应该选哪个。高光的空间变化一般比形状更重要。既然这样,使用Phong的NDF像是最简单的,它的计算简单,表现力合理。如果需要更真实的高光效果,那么Trowbridge-Reitz是和不错的选择,它的“宽边帽”形状像是比高斯Phong瓣更接近真实世界的材质。Trowbridge-Reitz还有个优势就是已经成功地应用到了电影和游戏中[10, 38, 54, 59]。如果需要更惊艳的NDF,那么在刚刚被讨论过的2参数各向同性NDF(译者注:就是刚刚省略的ABC,SGD和GTR)中,我推荐GTR分布。它比另2种简单点,也成功地用到过电影上[10]。但是,艺术家操作这样的NDF的空间分布是比较难的。一种可能的帮助是,减少参数空间的维度(定义一个一维空间——基于艺术家的品味或材质数据——然后向艺术家暴露一个参数线。另一个可能的帮助是,只暴露一个参数,将另一个设置为对每种材质分别为一个常量。这样,一个再参数化功能就可用了,用来更干净地区分开“光滑度”和“形状”。一个可能用的到的研究是,使用概率分布的统计量,例如方差和峰态(似乎对应了可视化的“光滑度”和“尖刺度”)。
选择几何函数
未完待续。。
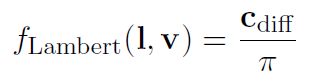

![[译]背景:着色的物理和数学(3)_第1张图片](http://img.e-com-net.com/image/info8/53ebfeea114c4288b3d4aa314ea2f66b.jpg)
![[译]背景:着色的物理和数学(3)_第2张图片](http://img.e-com-net.com/image/info8/34513b5d5a54478a99412cc50f3506f9.jpg)
![[译]背景:着色的物理和数学(3)_第3张图片](http://img.e-com-net.com/image/info8/b6227912558444119cdf70d8ed3b7a4b.jpg)


![[译]背景:着色的物理和数学(3)_第4张图片](http://img.e-com-net.com/image/info8/c0af6c191c6b4c7aa3b5c6709192616a.jpg)
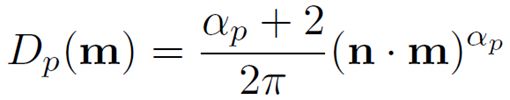
![[译]背景:着色的物理和数学(3)_第5张图片](http://img.e-com-net.com/image/info8/ee2e57254caa413497b8265d115a350a.jpg)
![[译]背景:着色的物理和数学(3)_第6张图片](http://img.e-com-net.com/image/info8/f343d1ff8d4d44e19761600113082ac4.jpg)
![[译]背景:着色的物理和数学(3)_第7张图片](http://img.e-com-net.com/image/info8/a16a6f0662ef4858a2584ecfcd09f77f.jpg)
![[译]背景:着色的物理和数学(3)_第8张图片](http://img.e-com-net.com/image/info8/60ee0c0201c043728961887136f3d040.jpg)

![[译]背景:着色的物理和数学(3)_第9张图片](http://img.e-com-net.com/image/info8/5dcf0e48c9cf4fe59608c1258c2c467c.jpg)
![[译]背景:着色的物理和数学(3)_第10张图片](http://img.e-com-net.com/image/info8/e5138db7acef4bf5b4069b9b8576cf2a.jpg)