Python 函数

一、函数的介绍

函数是组织好的，可重复使用的，用来实现单一，或相关联功能的代码段。

函数能提高应用的模块性，和代码的重复利用率。你已经知道Python提供了许多内建函数，比如print()。但你也可以自己创建函数，这被叫做用户自定义函数

函数的好处：

• 代码重用
• 保持一致，易于维护
• 可扩展性

二、函数的定义及调用

2.1 函数的定义

函数的定义规则：

• 函数代码块以 def 关键词开头，后接函数标识符名称和圆括号 ()
• 任何传入参数和自变量必须放在圆括号中间，圆括号之间可以用于定义参数
• 函数的第一行语句可以选择性地使用文档字符串—用于存放函数说明
• 函数内容以冒号起始，并且缩进
• return [表达式] 结束函数，选择性地返回一个值给调用方。不带表达式的return相当于返回 None

1 定义函数的语法：
2 
3 
4 def 函数名(参数):
5     函数体
6     返回值

1 # 示例
2 
3 def print_hello():
4     """
5     打印hello
6     :return:
7     """
8     print("hello")

2.2 函数的调用

定义了函数之后，就相当于有了一个具有某些功能的代码，想要让这些代码能够执行，需要调用它

调用函数很简单的，通过 函数名() 即可完成调用

1 # 示例：
2 print_hello()  # 调用函数

注意：

• 每次调用函数时，函数都会从头开始执行，当这个函数中的代码执行完毕后，意味着调用结束了
• 当然了如果函数中执行到了return也会结束函数

三、函数的返回值

在函数中添加返回值，需要使用return关键字

 1 def fun1():    # 无返回值
 2     print("aa")
 3 
 4 def fun2():
 5     msg = "hello world"
 6     return msg    # 返回msg，一个返回值
 7 
 8 def fun3():
 9     return 1, 2, 3    # 返回多个返回值
10 
11 aa = fun1()    # 接收函数的返回值
12 bb = fun2()
13 cc = fun3()
14 print(aa)
15 print(bb)
16 print(cc)
17 
18 # 输出结果：
19 # None
20 # hello world
21 # (1, 2, 3)

总结：

• 函数中如果没有return语句返回，那么python函数会默认返回None
• 函数返回值数为0，函数默认返回None；函数返回值数为1是，则返回object；返回值数大于1时，则返回的是一个tuple

四、函数的参数

 函数参数的原则：

• 形参变量只有在被调用时才分配内存单元，在调用结束时，即刻释放所分配的内存单元。因此，形参只在函数内部有效。函数调用结束返回主调用函数后则不能再使用该形参变量
• 实参可以是常量、变量、表达式、函数等，无论实参是何种类型的量，在进行函数调用时，它们都必须有确定的值，以便把这些值传送给形参。因此应预先用赋值，输入等办法使参数获得确定值
• 位置参数和关键字（标准调用：实参与形参位置一一对应；关键字调用：位置无需固定）
• 默认参数:放在参数列表的最后
• 参数组

4.1 普通参数

1 def fun1(name):   # name为形式参数
2     print(name)
3 
4 aa = "hello"
5 fun1(aa)  # aa为实参

4.2 默认参数

 1 def func(name, age=18):
 2     print("%s:%s" % (name, age))
 3 
 4 
 5 # 指定参数
 6 func('aa', 19)  # 自定义传入默认参数，以传入的为准
 7 func('cc', age=20)
 8 func('bb')      # 默认参数不传，使用默认值
 9 
10 # 运行结果：
11 # aa:19
12 # cc:20
13 # bb:18

4.3 动态参数

位置参数 > *动态参数 > 默认参数

 1 def func1(*args):
 2     print(args)
 3     print(type(args))       #   元组
 4 
 5 
 6 # 执行方式一
 7 func1(11, 33, 4, 4454, 5)
 8 
 9 # 执行方式二
10 li = [11, 2, 2, 3, 3, 4, 54]
11 func1(*li)

 1 def func2(**kwargs):
 2     print(kwargs)
 3     print(type(kwargs))     # 
 4 
 5 
 6 # 执行方式一
 7 func2(name='wupeiqi', age=18)
 8 
 9 # 执行方式二
10 dict1 = {'name': 'fyh', "age": 18, 'gender': 'male'}
11 func2(**dict1)

注意：

• 加了星号（*）的变量args会存放所有未命名的变量参数，args为元组
• 而加**的变量kwargs会存放命名参数，即形如key=value的参数， kwargs为字典

1 # 万能参数　　可以接收任意的参数
2 def func(*args, **kwargs):
3     pass

五、函数的嵌套

 1 def func1():
 2     print("hello world")
 3 
 4 
 5 def func2():
 6     print("aa")
 7     func1()         
 8     print("cc")
 9 
10 
11 func2()  # 按顺序执行 先执行print("aa") --> func1() --> print("cc")

六、全局变量与局部变量

6.1 命名空间与作用域

命名空间：
    1.内置命名空间：python解释内部运行时的变量函数
    2.全局命名空间：我们在py文件中直接声明出来的变量、函数
    3.局部命名空间：在函数内部声明的变量和函数

加载顺序：
    1.内置命名空间
    2.全局命名空间
    3.局部命名空间

取值顺序：
    1.局部命名空间
    2.全部命名空间
    3.内置命名空间


作用域：
    1.全局作用域：全局命名空间 + 内置命名空间
    2.局部作用域：局部命名空间
    可以通过globals()函数来查看全局作用域中的内容，也可以locals()查看当前作用域中的内容

6.2 全局变量与局部变量

全局变量与局部变量的本质在于作用域的不同

全局变量说白了就是在整个py文件中声明，全局范围内都可以使用

局部变量是在某个函数内声明的，只能在函数内部使用

 

1 # 示例
2 def fun1():
3     name = "aa"
4 print(name)

报错的原因：试图访问局部变量而报的错

6.2.1 局部变量和全局变量名一样

• 全局变量与局部变量名一致，函数内部会优先使用局部变量
• 修改局部变量不会影响到全局变量

 1 name = "bb"
 2 def print_name():
 3     name = "aa"
 4     print(name)
 5      
 6 print_name()
 7 print(name)
 8 # 打印的结果为
 9 # aa
10 # bb

6.2.2 global关键字

使用global关键字：则会告诉python编译器，这个变量是全局变量而不是局部变量，这样在函数体内修改变量会影响全局了

 1 name = "bb"
 2 def print_name():
 3     global name
 4     name = "aa"
 5     print(name)
 6 print_name()
 7 print(name)
 8 # 打印的结果:
 9 # aa
10 # aa

6.2.3 nonlocal关键字

nonlocal关键字在python3中新出现的关键字，作用：用来在函数或其他作用域中使用外层(非全局)变量

nonlocal适用于在局部函数中的局部函数，把最内层的局部变量设置成外层局部可用，但是还不是全局的。

注：nonlocal必须要绑定局部变量

 1 def fun1():
 2     num = 1
 3 
 4     def fun2():
 5         nonlocal num    # 此处不能使用global，只能使用nonlocal
 6         num += 1
 7         return num
 8     return fun2
 9 
10 
11 aa = fun1()
12 print(aa())

七、函数名的本质

函数名本质上就是函数的内存地址

7.1 可以被引用

1 def func():
2     print('in func')
3 
4 
5 f = func
6 print(f)    # 

7.2 可以被当作容器类型的元素

 1 def f1():
 2     print('f1')
 3 
 4 
 5 def f2():
 6     print('f2')
 7 
 8 
 9 def f3():
10     print('f3')
11 
12 
13 l = [f1, f2, f3]
14 d = {'f1': f1, 'f2': f2, 'f3': f3}
15 # 调用
16 l[0]()
17 d['f2']()

7.3 可以作为函数的参数或返回值

7.3.1 作为函数的参数

1 def func1():
2     print("aa")
3 
4 
5 def func2(f2):
6     f2()
7 
8 
9 func2(func1)　　# 作为函数的参数

7.3.2 作为返回值

1 def func1():
2 
3     def func2():
4         print("bb")
5     return func2   # 作为返回值
6 
7 
8 f = func1()    
9 f()

八、匿名函数

语法格式：lambda [形参1], [形参2], ... : [单行表达式] 或 [函数调用]

1 # 不带参数
2 my_fun = lambda : 10 + 20
3 # 带参数
4 my_add = lambda a, b: a + b
5 my_add()

注意：

• 函数的参数可以有多个，多个参数之间用逗号隔开
• 匿名函数不管多复杂，只能写一行，且逻辑结束后直接返回数据
• 返回值和正常的函数一样，可以是任意数据类型

 

匿名函数并不是说一定没有名字，这里前面的变量就是一个函数名。说它是函数名原因是我们通过__name__查看的时候是没有名字的，统一是lambda.在调用的时候没有什么特别之处，像正常函数一样调用即可。

 

匿名函数作为函数参数

 1 def my_function(func):
 2 
 3     a = 100
 4     b = 200
 5     # 把 cucalate_rule 当做函数来调用
 6     result = func(a, b)
 7     print('result:', result)
 8     
 9 
10 my_function(lambda a, b: a + b)

九、高阶函数

9.1 sorted 排序

语法：sorted(Iterable, key=None, reverse=False)
            Iterable:可迭代对象
            key：排序规则(排序函数)，在sorted内部会将可迭代对象中的每一个对象传递给这个函数的参数，根据函数的运算结果进行排序

 1 lst = [5, 7, 6, 12, 1, 13, 9, 18, 5]
 2 # lst.sort()  # sort是list里面的方法
 3 # print(lst)
 4 new_lst = sorted(lst, reverse=True)     # 内置函数，返回给你一个新列表,新列表是被排序的
 5 print(new_lst)
 6 
 7 
 8 # 给列表排序，按照字符串的长度进行排序
 9 lst2 = ["大阳哥", "尼古拉斯", "赵四", "刘能", "广坤", "谢大脚"]
10 
11 
12 def func(st):
13     return len(st)
14 
15 
16 new_lst = sorted(lst2, key=func)     # 内部，把可迭代对象中的每一个元素传递给func
17 # new_lst = sorted(lst2, key=lambda x: len(x))    # 也可以使用匿名函数
18 print(new_lst)

9.2 filter 过滤

filter(过滤)：遍历序列中的每个元素，判断每个元素得到布尔值，如果是True则留下来，组成新的迭代器
语法：filter(function, Iterable) 返回一个迭代器
            function:用来筛选的函数，在filter中会自动的把iterable中的元素传递给function，然后根据function返回的True或者False来判断是否保留次数据
            Iterable:可迭代对象

1 list1 = ["1111aaa", "2222aaa", "3333aaa", "4444", "5555", "6666"]
2 list2 = filter(lambda x: x.endswith("aaa"), list1)  # 有过滤的作用
3 print(list(list2))
4 # 运行结果：['1111aaa', '2222aaa', '3333aaa']

9.3 map 映射

    语法:map(function, Iterable)
        map处理序列中的每个元素，得到一个结果(迭代器)，该迭代器元素个数与位置不变

 1 list1 = [1, 2, 3, 4, 5]
 2 list2 = map(lambda x: x+1, list1)  # map的第一个参数为函数，后面的参数为可迭代对象
 3 print(list(list2))
 4 # 结果：[2, 3, 4, 5, 6]
 5 
 6 lst1 = [1, 2, 3, 4, 5]
 7 lst2 = [2, 4, 6, 8, 9]
 8 
 9 
10 print(list(map(lambda x, y: x+y, lst1, lst2)))
11 # 结果：[3, 6, 9, 12, 14]

9.4 reduce

reduce 处理一个序列，把序列进行合并操作

from functools import reduce
list1 = [1, 2, 3, 4, 5]
aa = reduce(lambda x, y: x+y, list1)  # 前一个参数的函数必须是两个参数
print(aa)
# 运行结果：15

 十、递归函数

1、递归的特点

递归算法是一种直接或间接调用自身算法的过程，在计算机编程中，递归算法对解决一大类问题是十分，它往往使算法的描述简洁而且易于理解。

递归算法解决问题的特点：

（1）递归就是在过程或函数里调用自身

（2）在使用递归策略时，必须有一个明确的递归结束条件，称为递归出口。

（3）递归算法解题通常显得很简洁，但递归算法解题的运行效率较低，所以一般不提倡用递归算法设计程序。

（4）在递归调用的过程中系统为每一层的返回点、局部量等开辟了栈来存储，递归次数过多容易造成栈溢出等。

 

2、递归的要求

递归算法所体现的“重复”一般有三个要求：

（1）每次调用在规模上都有所缩小（通常是减半）

（2）是相邻两次重复之间有紧密的联系，前一次要为后一次做准备（通常前一次的输出作为后一次的输入）

（3）在问题的规模极小时必须用直接给出解答而不再进行递归调用，因而每次递归调用都是有条件的（以规模位达到直接解答的大小为条件）无条件递归调用将会成为死循环而不能正常结束。

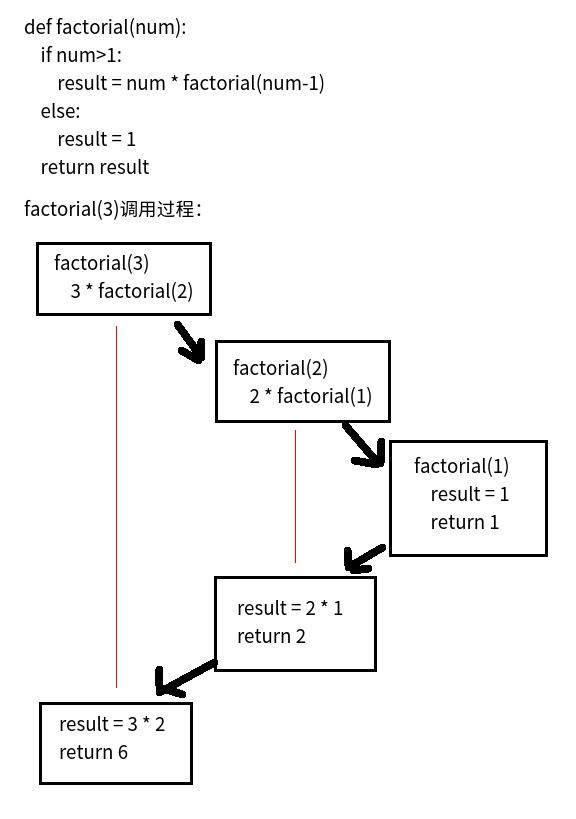
 1 """
 2 1! = 1
 3 2! = 2 × 1 = 2 × 1!
 4 3! = 3 × 2 × 1 = 3 × 2!
 5 4! = 4 × 3 × 2 × 1 = 4 × 3!
 6 ...
 7 n! = n × (n-1)!
 8 使用递归实现
 9 """
10 
11 
12 def cal_num(num):
13     if num >= 1:
14         result = num * cal_num(num - 1)
15     else:
16         result = 1
17     return result
18 
19 
20 print(cal_num(3))

执行原理：

 

递归的执行深度调整：

1 import sys
2 sys.setrecursionlimit(10000)    # 可以调整递归深度，但是不一定跑到这里

# 斐波那契数列：就是前两个数的和为后一个数的值（0，1，1，2，3，5，8，13.........）:
# 计算第n个数的值

def foo(num):
    """
    实现斐波那契数列
    :param num: 第几个数
    :return:
    """
    if num <= 0:
        return 0
    elif num == 1:
        return 1
    else:
        return foo(num - 1) + foo((num - 2))

递归实现斐波那契数列