五、改进神经网络的学习方法（1）：交叉熵代价函数

本博客主要内容为图书《神经网络与深度学习》和National Taiwan University (NTU)林轩田老师的《Machine Learning》的学习笔记，因此在全文中对它们多次引用。初出茅庐，学艺不精，有不足之处还望大家不吝赐教。

1. 均方误差函数的局限性

  在之前的博客《三、神经网络的训练》中介绍过代价函数，在那一节中为了方便理解，采用了常用的均方误差函数作为代价函数，但实际应用中却有着很大局限性。采用均方误差作为代价函数会使得神经网络在输出结果错误很大的情况下仍仅具有较小的参数更新速度，使得神经网络的训练变得困难。
  我们从原理上考虑出现这种情况的原因，参数的更新速度较慢体现在神经网络中就是偏导数的值很小。从反向传播的四个基本等式入手，考虑其中后三个等式，如 (1)

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪δ l=((w l+1)Tδ l+1)⨀σ′(z l)∂C∂blj=δj l∂C∂wjkl=al−1kδlj(1)

从中可以明显看出 σ′(z) 对于函数的导数值影响很大，当sigmoid函数的输出值接近于1或者0的时候， σ(′z) 的值会近似于0。这就是网络更新参数的速度变得很慢的根源，也就是均方误差函数中的局限性。
  为了加深理解，在此对均方误差函数的局限性进行举例说明，比如说现在输入数据的期望输出（实际类别）为1，如果此时神经网络的输出值也接近于1，虽然此时的学习速度也会很慢，但这是我们可以忍受的，因为已经很靠近真实值了；但是如果输出值为0，此时对于分类问题来讲是一个很大的分类错误，但是此时的学习速度仍然是缓慢的，是我们无法忍受的。也就是说局限性具体表现在对于输出错误较大，而参数学习速度却很慢这件事情上。

2. 交叉熵代价函数简介

2.1 什么是交叉熵函数

  定义交叉熵函数的形式如公式 (2) 所示

C=−1n∑x[ylna+(1−y)ln(1−a)](2)

这个函数特点在于当神经网路的输出值与期望的输出值较为接近的时候，函数值近似为零，所以常常认为交叉熵是对惊讶程度的测度。假设我们将神经元的输出值 a 当作根据输入的 x 预测输出值是 y=1 的概率，很明显 1−a 是预测输出值是 y=0 的概率，而交叉熵就是衡量我们知道期望输出值后的平均惊讶程度。如果输出我们期望的结果，平均惊讶程度（即不确定性）就会⼩⼀点；反之，平均惊讶程度（即不确定性）就⼤⼀些。
  在刚接触交叉熵时，很难⼀下⼦记住那些诸如 y 和 a 的表达式对应的位置，有时会写成如下的错误形式

C=−1n∑x[alny+(1−a)ln(1−y)](3)

这是一种明显的错误形式，主要原因在于当 y 的取值为0或者1的时候表达式是违法的，而 a 的值是无限接近于0和1但不能达到0和1的，因此不是违法的。同样的，我们可以利用这个特性对交叉熵函数的表达式进行记忆。

2.2 为什么交叉熵函数可以做代价函数

  交叉熵函数可以做代价函数的原因主要有三点，前两点是与均方误差函数的相似性，而最后一点是其独有的优点。

• 非负性
  (2) 中的求和中的所有独⽴的项都是负的，因为对数函数的定义域是(0,1)，且求和前⾯有⼀个负号，因此整个等式是满足非负性的。
• 可解释性
  如果对于所有的训练输⼊ x ，神经元实际的输出接近⽬标值，那么交叉熵将接近0，与之前的代价函数具有相似的含义。
• 避免学习率降低
  为了证明在神经网络中交叉熵函数可以避免学习率降低，我们需要计算交叉熵函数关于权重的偏导数。在这里仅仅使用一个简单的多输入神经元为例进行说明，用 a=σ(z) 代替等式，应用链式法则对代价函数的权重求偏导数，因为只有一个神经元，所以 wj 就是某一个权重，而不是代表某一层权重的向量，这一点与之前讲的有所不同，通过计算得到如下的结果
  
  ∂C∂wj=−1n∑x(yσ(z)−(1−y)1−σ(z))∂σ∂wj=−1n∑x(yσ(z)−(1−y)1−σ(z))σ′(z)xj(4)
  
  通分化简后可以得到
  
  ∂C∂wj=−1n∑xσ′(z)xjσ(z)(1−σ(z))(σ(z)−y)(5)
  
  由于在sigmoid函数中 σ′(z)=σ(z)(1−σ(z)) ，所以上式可以化简为
  
  ∂C∂wj=−1n∑xxj(σ(z)−y)(6)
  
  这样的表达式告诉我们权重的学习速率可以被 (σ(z)−y) 控制，也就是被输出结果的误差所控制，误差越大我们的神经元学习速率越大；另外它通过消去 σ′(z) 避免学习减速。
    如果同样对神经元的偏置值求偏导数也具有相似结构，如
  
  ∂C∂bj=−1n∑x(σ(z)−y)(7)
  
  通过分析可知对于偏置值也有同样的性质。
    那什么情况下我们要用交叉熵函数取代均方误差函数呢？事实上，如果输出神经元是sigmoid神 经元的话，交叉熵都是更好的选择。

2.3 在多层神经网络中的证明

  在上一小节中，已经证明了在多输入神经元中交叉熵函数可以避免学习减速， 接下来我们要证明对于多层的神经网络采用交叉熵代价函数仍然可以避免学习减速。
  假设 y=y1,y2,... 是我们期望的输出，在神经元的最后一层 aL1,aL2,... 是真实的输出，那么我们可以定义交叉熵

C=−1n∑x∑j[yjlnaLj+(1−yj)ln(1−aLj)](8)

在这里的双层求和符号首先对内层求和，即对所有的神经元的输出求和，其次在对所有的训练数据求和。利用均方误差函数对输出层某一个权重的偏导数，这里已经将均方误差函数带入，根据反向传播四个基本等式中的第一个和最后一个，得到如下形式

∂C∂wLjk=1n∑xaL−1k(aLj−yj)σ′(zLj)(9)

其中 σ′(zLj) 会导致当输出明显出错的时候学习速度下降。但是对于交叉熵函数

δL=∂C∂z=−1n∑xσ′(z)σ(z)(1−σ(z))(σ(z)−y)=aL−y(10)

将其带入四个基本等式中的最后一个等式可得

∂C∂wLjk=1n∑xaL−1k(aLj−yj)(11)

  这样 σ′(zLj) 这一项就消去了，因此交叉熵代价函数能够避免学习减速，简单变形一下也能得到偏移也具有相同的形式。

  对于学习减速这个问题考虑使用另一种方式进行改进，即采用线性神经元，输出 aLj=zLj ，但仍保持代价函数为均方误差函数，这时 σ′(zLj)=1 ，同样可以避免学习减速。

2.4 为什么会想到交叉熵函数

  假设此时的代价函数为均方误差函数，则

∂C∂wj=（a−y）σ′(z)xj(12)

根据上文可知，产生学习减速现象的主要原因是 σ′(z) 的存在，因此如果存在某一个代价函数使得 σ′(z) 项消失，便可以避免学习减速现象的出现，这样代价函数对于权重的偏导数就会变为

∂C∂wj=（a−y）xj(13)

而另一方面

∂C∂wj=∂C∂aσ′(z)xj=∂C∂aa(1−a)xj(14)

将公式 (13) 和公式 (14) 联立可以得到

∂C∂a=a−ya(1−a)(15)

对两侧同时积分可以得到

C=−[ylna+(1−y)ln(1−a)]+constant(16)

因此对于所有的训练数据

C=−∑x[ylna+(1−y)ln(1−a)]+constant(17)

3. 交叉熵代价函数与均方误差函数的对比

  在本小节，我们采用单输入单输出的仅含有一个神经元的例子进行分析，此时的神经网络简化为如图1的形式

图1. 对比实验神经元示意图

实验结果如图2所示，图2左侧为均方误差代价函数随着迭代的变化情况，初始参数值设置为权重为0.6，偏移为 0.9，在这里学习率 η=0.15 ；图2右侧为交叉熵代价函数随着迭代的变化情况，初始参数值设置为权重为2，偏移为 2，在这里学习率 η=0.005 。

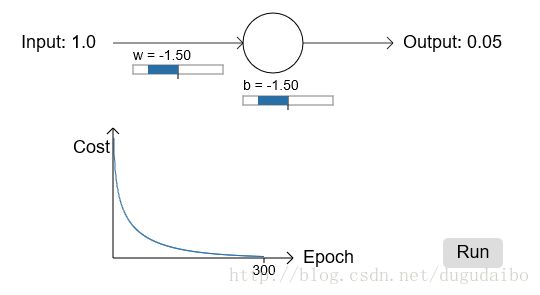
图2. 交叉熵代价函数与均方误差函数实验结果对比图

  通过比较初始参数可知，均方误差函数距离期望输出值更近，因此具有更好的初始值情况，而交叉熵函数初始值距离期望输出值较远，因此错误程度更大，但是通过实验可知，交叉熵代价函数曲线比使用均方误差函数的曲线更陡峭。这意味着即使我们初始的条件很糟糕，交叉熵函数也能尽可能地降 低学习速度减慢的可能性。
  其次是关于学习率的讨论，即为什么不对两者采用相同的学习率？主要原因在于对于不同的代价函数很难定义什么是相同的学习率（我的理解是相同的参数更新速度？），其次这部分实验主要是讨论一个错误程度较大的初始值对于学习速度的影响，因此可以不用太care相同的 η 这一点。对于这个问题我也有自己的理解，从参数上来看，交叉熵函数的 η 更小，理论上学习的速度应该更慢才对，但是他的速度却明显高于 η 更大的均方误差代价函数，这也就更强有力的证明了交叉熵函数不会像均方误差代价函数那样减小学习速率。
  有一种非常粗浅的想法找到交叉熵代价函数和平方代价函数两者的学习率的联系。正如我们之前所看到的，平方代价函数的梯度表达式中多一项 σ′=σ(1−σ) 。如果我们对 σ 算一下均值，我们得到 ∫10σ(1−σ)dσ=16 。我们可以大致上推断当学习率相同时，平方代价函数的速度会平均上慢6倍。这表明一个可行的方法是将平方代价函数的学习率除以6。当然，这远远不是一个严谨的推断，但是你也可以将其视为一种有用的初始化方法。