无监督学习：生成模型

National Taiwan University (NTU)李宏毅老师的《Machine Learning》的学习笔记，因此在全文对视频出现的内容多次引用。初出茅庐，学艺不精，有不足之处还望大家不吝赐教。

欢迎大家在评论区多多留言互动~~~~

1. 生成模型

  2016年PixelRNN，2014年Variational Autoencoder (VAE)，2013年Generative Adversarial Network (GAN)。

2. Pixel RNN

  这种方法的主要过程如下所示

在训练的过程中，首先输入图像的第一个像素，这个时候NN的输出应该是图像的第二个像素；然后输出图像的第一、二个像素，这个时候NN输出的是图像的第三个像素，依次类推，对网络进行训练。假设我们给出了图像的一半，希望得到另一半的结果时，实验结果如下

如上图，最左侧的图像为原始图像，中间的为输入图像，已经将图像的一半遮盖住，希望补全另一半图像。后面是得到的三种结果，还算可以把。

  在训练上面这个网络的时候，一个直观的方法是将图像的 RGB 三个通道作为输入，但是这种方法得到的测试结果往往会偏灰色和棕色，这是因为神经网络的输出常常使得输出的三个值在数值上十分接近。因此在这里利用 1 of N encoding 对颜色进行编码，但是如果对所有颜色进行编码的话，总共有256256256种编码，维数过高，所以首先对颜色进行聚类，对聚在一类的颜色使用相同的编码，大大降低了编码的维数。

3. Variational Autoencoder (VAE)

3.1 VAE的过程

  自编码器在之前的博客中已经介绍了，主要的过程如下所示

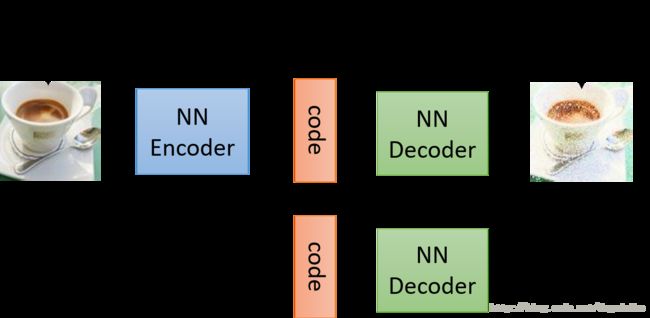
如果随机产生 code 然后经过 decode 之后是可以产生图像，但是要产生需要的图像，这个时候就需要VAE的帮助了。VAE的主要过程如下图所示

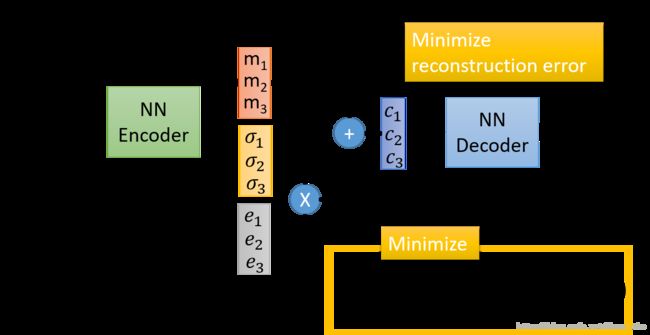
它的过程与 Aotuencoder 十分相似，前面的编码和后面的解码部分没有变化，中间的部分是添加的部分。首先如果你中间的编码部分希望得到的维数是3维的话，那么就会输出一个三维的 m 和一个三维的 $\sigma$，同时利用正态分布生成一个相同维数的向量 $e$ ，经过计算得到编码 $c$（计算过程如上图所示），然后是解码的过程，最终的损失函数是同时最小化重建误差和下面的累加求和。
  下面是VAE的实验结果


可以看出来 VAE 想画点什么东西出来，但是并不知道 VAE 具体想画什么出来。那么他与pixel Rnn 的区别在于哪呢？在 VAE 中，可以如下图所示

假如我们中间编码的是一个十维的向量，那么可以保持其中的八维不变，变化其中的两维，看看这两维对于图像的影响是怎样的。具体的实验结果如下图所示

  或者也可以使用VAE写诗。将上面的的输入输出都改成 sentence，之后如下图所示

随便输入两个句子，找到它们的编码向量，在两个向量之间做一条连线，在连线上等间距的取若干个点（即一些编码），将这些编码进行解码就可得到对应的句子。

3.2 为什么要用VAE的直观解释

  从直观的理解为什么使用VAE，与之前的自编码的区别在于哪里呢？

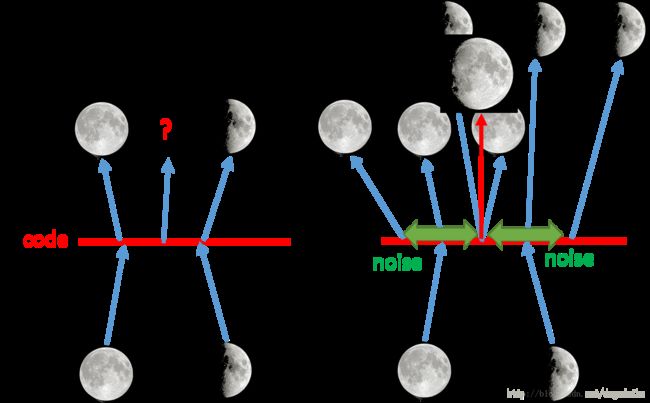
如上图，左侧是自编码过程，右侧是VAE过程。如果在左图中，取满月和弦月编码的之间点，输出的结果是怎么样的，会不会是介于两者之间的月相是不好说的。但是如果采用VAE的方法，他实际上相当于在编码的时候向里面加入了噪声，使得含有噪声的图像仍然可以恢复为原来的图像，那么加入取两者中间重叠的点，这个时候由于损失函数要使得恢复的误差最小，这样就需要综合满月和弦月的图像，很有可能就得到介于两者之间的图像。

  加入噪声的原理如下图所示

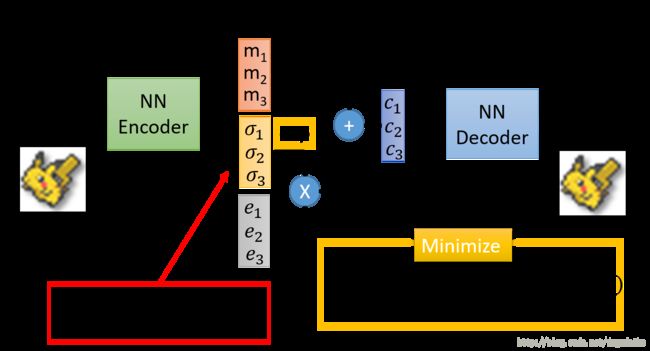
其中的 $m$ 可以认为是原始的编码，而 $\sigma$ 认为是方差，$e$ 本身是从正太分布得到的，所以本身有固定的方差，将两者相乘相当于向编码中加入方差为某一个值的噪声，其中$e$ 要取指数，这个时候就可以保证所得到的方差是整数的，而且又由于 $\sigma$ 是通过网络得到的，所以网络在学习中可以自动调节噪声方差的大小。

  在训练这个网络时，不仅仅只是用之前的重建误差最小，还需要加入如上图中的那一项。因为如果让网络自己随便学习的话，他会倾向于不在网络中加入噪声，如果这样的话他就与之前的自编码器没有区别了，所以需要加入如下图的惩罚项。

其中蓝色的那一项如图中的蓝色的曲线所示，途中红色的项如图中红色的曲线所示，两项相减得到的结果如图中的绿色曲线所示。我们可以看到，如果要使这一项取到最小值需要使得 ${\sigma }_i$ 的值为0，这个时候 $exp（{\sigma }_i）$的值为1，而不是零，这样就可以保证加入模型中的方差不是0，即有噪声加入网络中。其中的 $m$ 直接认为是正则项就好，可以增强模型鲁棒性。

3.3 从VAE的原理解释为什使用VAE

  回到问题的本身，我们实际上是希望生成图像。假如我们将图像看作是高维空间上的一个点，那么我们需要的就是估计这些点在高维空间的分布，这个概率分布的大概的形式应该如下图所示

它在有宝可梦存在的地方的概率应该比较高，在没有宝可梦的区域应该比较低。所以可以从概率比较高的部分进行抽样，生成新的数据。

  而估计概率这件事情可以使用高斯混合模型。高斯混合模型可以大概表示为下图的样子

其中黑线是高斯混合模型的概率密度曲线，它是由许许多多个高斯模型按照一定的权重混合得到的。那如何从这样的混合模型中进行采样呢？首先我们选取从组成高斯混合模型的若干个高斯分布中选择使用哪一个高斯分布，然后对于选定的某一个高斯分布，他有着自己的均值和方差 ${\mu }^m,{\Sigma }^m$ ，根据他的均值和方差，就可以从中采样。

  对于高斯混合模型中参数的估计，实际上可以利用数据通过EM算法进行估计。

  实际上，之前有讲过，对数据进行聚类的话，不如对数据进行分布式的表示，有多少的概率属于A，有多少的概率属于B等等……而本是上，VAE就是高斯混合模型的分布表示的形式

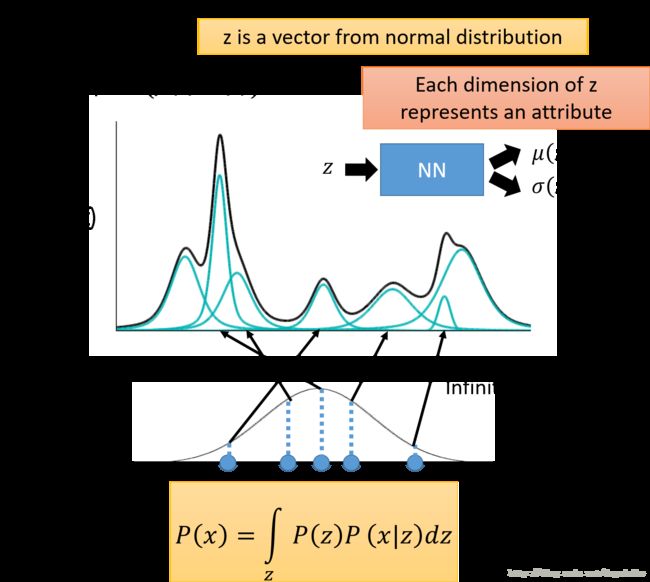
假设 $z$ 服从某一个标准概率分布，从这样的分布中采样若干个点，其中 z 可能是一个多维的向量，每一个维度代表一个属性。以一个 1 维的高斯分布为例，我们从中采样出一个 z ，然后根据 z 决定所对应的高斯分布的均值和方差 $\mu (z),\sigma (z)$ ，在这里我们的 z 有无穷种可能，不想之前的混合模型中只是几种高斯模型的混合。所以现在给定了某一个 z 那么如何得到对应的均值和方差呢？这里我们假设均值和方差是通过一个函数得到的，就是说给定一个输入 z 就会得到一个均值和方差（实际上就是一个高斯分布）。所以可以认为它们是通过一个神经网络的均值和方差（也就是说输入一个 z 输出可一个对应的高斯分布）。所以 $P(x)$ 的表示方式就如上图所示。

  在下面的这个用来采样的分布不一定非要是一个标准的高斯分布，可以是任何分布。因为NN是powerful 的，它可以通过神经网络得到。

  因为在下图中的式子中，我们需要估计 $\mu (z),\sigma (z)$ 是怎样的，所以就需要用极大似然估计的方法，这个等式等价于在其中加入一个关于 $q(z|x)$ 的积分，通过化简可以看到其中的一项是两个概率之间的KL距离，它明显是大于０的，所以得到了最大似然表达式的下限。

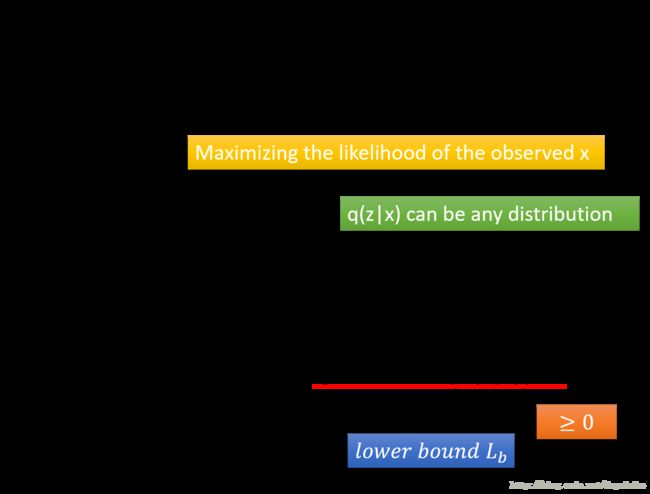
那为什么要引入 $q(z|x)$ 这一项呢？主要原因如下图所示

  首先假设没有加入 $q(z|x)$ 这一项，这个时候如果知识通过 $P(z|x)$ 进行调节的话，虽然可以使得 $L_b$ 上升，但是它只是下界，它上升了并不能保证函数值一定上升，也有可能会下降。但是如果引入 $q(z|x)$ 这一项，我们可以看到 $logP(x)$ 这一项的大小并不会改变，因为他的大小只与 $p(x|z)$ 这一项的大小相关，调整 $q(z|x)$ 可以保证 $logP(x)$ 的大小不变。调整 $q(z|x)$ 使得 $L_b$ 上升，此时 KL 的值就会逐渐下降，最后 $L_b$ 的值就可以近似的表示 $logP(x)$ 的值，这个时候如果再调整$p(x|z)$ 使得 $L_b$ 上升，就一定会导致 $logP(x)$ 上升，达到最大化 $logP(x)$ 的目的。同时我们可以看到最后可以使用 $q(z|x)$ 来近似估计 $p(z|x)$ 的大小。

  因为在调整的过程中，KL最后肯定是要接近于0的，所以最大化 $logP(x)$等价于最大化 $L_b$ ，对于它接着进行分解，如下图所示

化简得到的两项，首先第一项实际上又是一个 KL 距离的相反数，这项的实际含义就是，给定一个 x 希望得到一个分布，这个分布与 $P(z)$ 最为相似，这个也可以通过一个神经网络得到，网络的输入是 x ，网络的输出是分布的均值和方差。

所以最大化 $L_b$ 等价于最小化第一项的同时，最大化第二项，这个过程可以表示为如下的过程

最小化第一项已经说了可以用神经网络进行表示，并且就是最小化图中黄色的那个部分；最大化第二项实际上可以认为是在给定 x 生成 z 的时候，它再生成 x 可以得到最大的期望，这实际上就是一个自编码的过程。因此整个过程的证明就是这样的。

3.4 VAE存在的问题

  VAE主要的问题在于，他一直希望能够模仿已经存在的数字，而不是希望真正的生成一张图像，如下图所示

假设生成的图像与原始的图像只有一个像素的差距，这个像素的位置有如图中的两种可能，可以明显看出左侧的那个图是更现实的，而右侧的图明显比较假，但是对于VAE来说这两张图象之间的loss很有可能是一样的，所以才会导致这样的问题。为了解决这个问题，才有后文的 GAN 模型。

参考