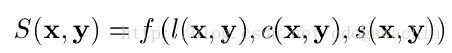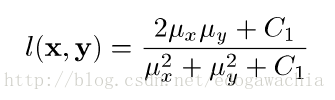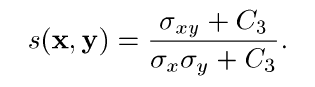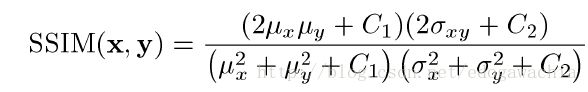图像质量评估指标 SSIM / PSNR / MSE

图像质量评估指标 SSIM / PSNR / MSE

Visibility of Errors

计算图像degrade后的质量，最 direct 的思路即比较degrade后的图像与真实图像（distortion-free）之间的差剖面，即可视误差，通过 visibility of errors 评价图像质量。

PSNR 和 MSE 就是基于这种简单直接的思路确定的指标，MSE（Mean Squared Error），顾名思义，定义略。PSNR（Peak Signal to Noise Ratio），峰值信噪比，即峰值信号的能量与噪声的平均能量之比，通常表示的时候取 log 变成分贝（dB），由于 MSE 为真实图像与含噪图像之差的能量均值，而两者的差即为噪声，因此 PSNR 即峰值信号能量与 MSE 之比。定义式如下：

$$PSNR=10lo{g}_{10}\frac{MaxValu{e}^2}{MSE}=10lo{g}_{10}\frac{2^{bits}-1}{MSE}$$

第二个等式由于图像像素点数值以量化方式保存，bits 即每个像素点存储所占的位数。因此 MaxValue 即为 2^bits - 1。

• 计算PSNR

    def cal_psnr(im1, im2):
        mse = (np.abs(im1 - im2) ** 2).mean()
        psnr = 10 * np.log10(255 * 255 / mse)
        return psnr
  

由于 grayscale 存成 8bit ，故最大值255。

Structural Similarity

由于基于差剖面的简单计算不符合人类视觉系统（Human Visual System，HVS）的评价结果，因此需要对评价方式进行重新考量。如果图片的最终目的是对人类展示的话，那么质量应该以人的主管测评为准。但是由于主管评价不方便且费时，因此我们试图用客观的 image quality assessment 来对图像进行评价，使其接近 HVS 的特点。由于 HVS 具有可以抓取图像的结构特征的特点，因此设计 Structural Similarity 进行评价，即 SSIM 。

图像质量评价分为：

1. full-reference：知道noise-free的图像。
2. no-reference：真实图像无法取得，因此需要blind assessment。
3. reduced-reference：reference只是部分的available。只有extracted features作为附加信息，进行评估。

这里讨论的是full-reference。

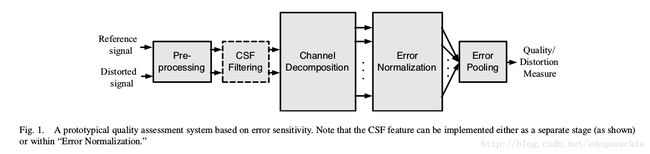
在介绍SSIM之前，由于MSE的缺点，人们尝试过对MSE进行改进，使得errors are penalized in accordance with their visibility。即 error sensitivity，基于误差敏感度。基本流程如下：

预处理比如，将色彩空间转换到更适合HVS的空间，将储存的像素值转换为显示出的亮度值，等等。CSF为 Contrast Sensitivity Function，该函数描述了HVS对于不同时空频带的刺激的敏感性。然后分成不同channel，或称为subband，根据方向，时空频率等等。再分别计算误差并normalize，然后combine。

然而上述方法有很多缺陷，因此考虑新的思路，从自然图像高度结构化的特征出发，设计新的assessment。

相比于之前估计 perceived errors，该思路估计 perceived changes in structural information variation。如下图所示，虽然这些图的MSE相同，即具有相同的PSNR水平，但是显然对于人的主管感觉来说差别时很大的，对于contrast的stretch，以及均值的偏移，即整体上明暗变化，基本上并不会影响人类对图像的内容的理解。因此应该让这样的图片得到的质量值更高。原因在于我们可以把original information近乎完全的恢复出来，只需要做pixel-wise的映射即可。（当然saturation的那些数值无法恢复），而像比如blur，JPEG compression等，许多结构信息已经永久丢失了，因此应该评分低些。从图可以看出，SSIM做的较好。

然后SSIM的基本思路是，通过一下三个方面来对两幅图像的相似性进行评估，即

1. luminance，亮度
2. contrast，对比度
3. structure，结构

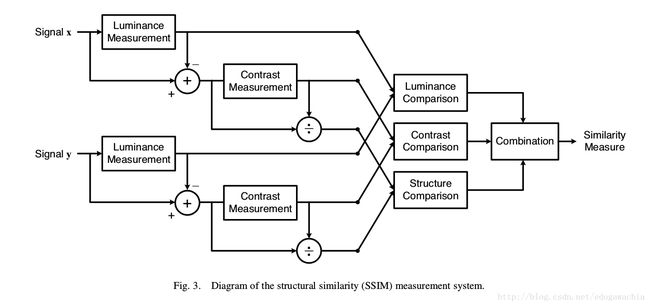
算法的框图基本如下：

基本流程为：对于输入的x和y，首先计算出luminance measurement，进行比对，得到第一个相似性有关的评价；在减去luminance的影响，计算contrast measurement，比对，得到第二个评价；在用上一步的结果除掉contrast，在进行structure的比对。最后将结果combine，得到最终的评价结果。

从实现角度来讲，亮度用均值表征，对比度用经过均值归一化之后的方差表征，结构用相关系数（就是统计意义上的 r ，协方差与方差乘积的比值）。

具体的计算公式如下所示：

其中S表示相似度，这个算子应当满足作为度量的基本性质，即

1. Symmetry，交换x和y顺序不影响结果。
2. Boundedness，值要有界，这里时小于等于1.。
3. Unique maximum，最大值，即1，只有当 x = y 时候取到。

上面的公式里，比如 l(x,y) ，这样定义的一个原因是让上下次数相同，然后可以满足Weber’s law，Weber定理说的是，对于HVS，对于亮度变化的最小感知的幅度与背景亮度成正比，也就是说，我们的视觉系统时对于相对的亮度变化敏感，而不是绝对值，比如我们的$\mu \_1$和$\mu \_2$如果是成比例的话，假设比例系数为(1+R)，带入计算，发现$ l(x,y) $ 仅仅与R有关，与两均值的绝对数值无关，说明我们的评价比较类似人眼的视觉的主观性质。然后后面的C_1常数项是为了当均值接近0的时候避免波动。对比度相似度的定义类似，然后结构相似性用的是correlation coefficient，也加了常数项防止除0。最后将三项加权乘积，一般选$\alpha =\beta =\gamma =1$ 使得表达式简单。于是总公式就是：

但是由于SSIM应该应用于局部，这既是因为图像distortion的程度可能空变，也是为了拟合人类视觉的局部性的特点，因此实际上我们用 mean-SSIM或者MSSIM，对各个local window的SSIM求平均。一般用高斯加权函数对每个local statistics进行加权防止出现blocking。

关于用SSIM测试的实验结果，作者首先做了一个很有趣的实验，即best/worst case的实验，通过对一个corrupted图像在保持MSE不变的情况下，对SSIM这个参数进行向上和向下的优化，找到了同等PSNR下的SSIM 最好和最差的情况。这样可以看出SSIM到底是表征了什么信息。

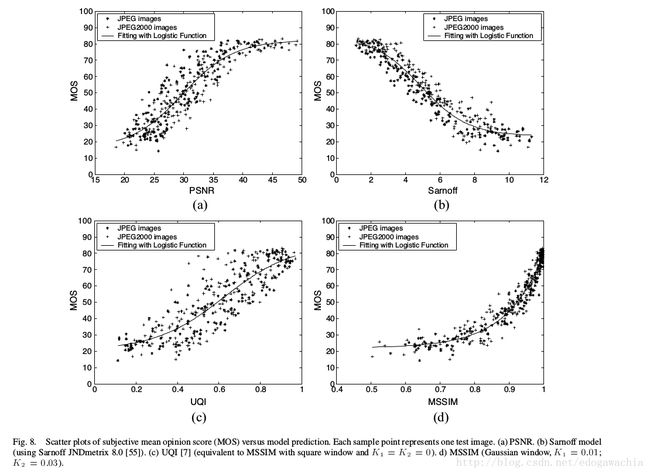
最后是和MOS (mean opinion score)的相关性。可以看出MSSIM效果更好一些，由于分布比较紧致。

• 计算SSIM

    def cal_ssim(im1,im2):
        assert len(im1.shape) == 2 and len(im2.shape) == 2
        assert im1.shape == im2.shape
        mu1 = im1.mean()
        mu2 = im2.mean()
        sigma1 = np.sqrt(((im1 - mu1) ** 2).mean())
        sigma2 = np.sqrt(((im2 - mu2) ** 2).mean())
        sigma12 = ((im1 - mu1) * (im2 - mu2)).mean()
        k1, k2, L = 0.01, 0.03, 255
        C1 = (k1*L) ** 2
        C2 = (k2*L) ** 2
        C3 = C2/2
        l12 = (2*mu1*mu2 + C1)/(mu1 ** 2 + mu2 ** 2 + C1)
        c12 = (2*sigma1*sigma2 + C2)/(sigma1 ** 2 + sigma2 ** 2 + C2)
        s12 = (sigma12 + C3)/(sigma1*sigma2 + C3)
        ssim = l12 * c12 * s12
        return ssim
  

THE END

星期六, 09. 十二月 2017 12:24上午

reference:
Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE transactions on image processing, 2004, 13(4): 600-612.