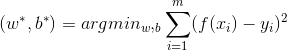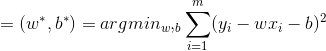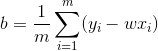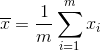pytorch学习笔记(线性模型)

线性模型

问题介绍

        线性模型,通俗来讲就是给定很多个数据点,希望能够找到一个函数来拟合这些数据点令它的误差最小,比如简单的一元函数就可以来表示给出一系列的点，找一条直线，使得直线尽可能与这些点接近，也就是这些点到直线的距离之和尽可能小。用数学语言来严格表达 ，即 给定由 d 个属性描述的示例 x = (x1，x2 ，x3 ， ...，xd) ' 其中 Xi 表示X在第i个属性上面的取值， 线性模型就是试图学习 一个通过属性的线性组合来进行预测的函数，即一元线性模型非常简单，每个$i$对应于一个数据点，希望建立一个模型 ,其中 ,y一般可以用向量来表达:

                                                                                     

w=(w1,w2,...,wd)和b都是要学习的参数,模型通过不断地调整w和b,最后就能得到一个最优的模型.

一维线性回归

给定数据集，线性回归希望能够优化出一个好的函数，使得能够和尽可能接近。

如何才能学习到参数w和b呢？很简单，只需要确定如何衡量与之间的差别，一般通过损失函数（Loss Funciton)来衡量：

取平方是因为距离有正有负，我们希望将它们变为全是正的。这就是著名的均方误差。基于均方误差最小化来进行模型求解的办法也称为"最小二乘法",我们要做的事情就是希望能够找到和，使得：

均方差误差非常直观，也有着很好的几何意义，对应了常用的欧式距离。现在要求解这个连续函数的最小值，我们很自然想到的方法就是求它的偏导数，让它的偏导数等于0来估计它的参数，即：

求解以上两式，我们就可以得到w和b的最优解：

其中

多维线性回归

有d个属性,试图求得最优化的函数f(x):

                                   

使得

最小,这称为"多元线性回归",同样可以用最小二乘法对w和b进行估计,为了方便计算,可以将w和d写进同一个矩阵,将数据集D表示成一个mx(d+1)的矩阵X,每行前面d个元素表示d个属性,最后一个元素设为1,将目标y也写成写成向量形式：y=(y1;y2;...;ym),然后就可以得到

对其求导,令它等于0.

若是一个满秩矩阵或者正定矩阵,那么我们可以得到:

所以线性回归模型可以写成: 

但是在现实中,往往不是满秩,即使是,求解逆的过程也比较慢,所以我们一般使用梯度下降的方法去求解这个最小二乘法的问题.

多项式回归

对于一般的线性回归,由于函数拟合出来的是一条直线,所以精度欠佳,我们考虑多项回归.提高每个属性的次数,而不是使用一次去回归目标函数.

拟合我们想要拟合的方程:

然后可以设置参数方程:

首先将数据变成一个矩阵的形式

接下来用pytorch来实现:

import torch
import numpy as np
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
import random
import matplotlib.pyplot as plt

def make_features(x):
    # 将矩阵扩展成多维式子
    '''BUild features i.e. a matrix with columns[x,x^2,x^3].'''
    x = x.unsqueeze(1) # unsqueeze(1) 是将原来的tensor大小由3变成(3,1)
    return torch.cat([x ** i for i in range(1, 4)], 1)


# 定义好真实的函数
w_target = torch.FloatTensor([0.5,3,2.4]).unsqueeze(1)
b_target = torch.FloatTensor([0.9])


def f(x):
    """Approximated  function."""
    return x.mm(w_target)+b_target[0]


def get_batch(batch_size=32, random = None):
    """BUilds a batch i.e (x,f(x)) pair."""
    if random is None:
        random = torch.randn (batch_size)
    batch_size = random.size ()[0]
    # random = torch.randn(batch_size)
    # 返回一个张量，包含了从正态分布(均值为0，方差为 1，即高斯白噪声)中抽取一组随机数。 Tensor的形状由变量sizes定义
    x = make_features(random)
    y = f(x)
    if torch.cuda.is_available():
        return Variable(x).cuda(),Variable(y).cuda()
    else:
        return Variable(x),Variable(y)

# 通过上面的这个函数我们每次取batch_size这么多个数据点,然
# 后将其转成矩阵的形式,再通过这个值通过函数之后的结果也返回作为真实的坐标

# 然后定义多项式模型


# Define model
class poly_model(nn.Module):
    def __init__(self):
        super(poly_model, self).__init__()
        self.poly = nn.Linear(3, 1)

    def forward(self,x):
        out = self.poly(x)
        return out


if torch.cuda.is_available():
    model = poly_model().cuda()
else:
    model = poly_model()


# 这里的模型输入时3维,输出是1维
# 这里定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-3)
# 开始训练模型
epoch = 0
while True:
    # Get data
    batch_x, batch_y = get_batch ()
    # forward pass
    output = model(batch_x)
    loss = criterion(output,batch_y)
    print_loss = loss.item()
    # reset gradients
    optimizer.zero_grad()
    # backward pass
    loss.backward()
    # update parameters
    optimizer.step()
    epoch +=1
    if print_loss <1e-3:
        break

# 定义函数输出形式
def func_format(weight, bias, n):
    func = ''
    for i in range(n, 0, -1):
        func += ' {:.2f} * x^{} +'.format(weight[i - 1], i)
    return 'y =' + func + ' {:.2f}'.format(bias[0])

predict_weight = model.poly.weight.data.cpu().numpy().flatten() # 因为使用了GPU所以要Use Tensor.cpu() to copy the tensor
predict_bias = model.poly.bias.data.cpu().numpy().flatten()
print('predicted function :', func_format(predict_weight, predict_bias,3))
real_W = w_target.numpy().flatten()
real_b = b_target.numpy().flatten()
print('real      function :', func_format(real_W, real_b,3))

x = [random.randint(-200, 200) * 0.01 for i in range(20)]
x = np.array(sorted(x))
feature_x, y = get_batch(random=torch.from_numpy(x).float())
print(feature_x.size())
y = y.data.cpu().numpy()
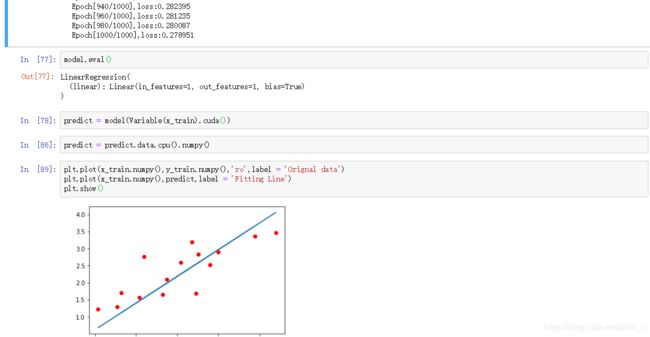
plt.plot(x, y, 'ro', label='Original data')

model.eval()
x_sample = np.arange(-2, 2, 0.001)
x, y = get_batch(random=torch.from_numpy(x_sample).float())
print(x.size())

y = model(x)
y_sample = y.data.cpu().numpy()
plt.plot(x_sample, y_sample, label = 'Fitting Line')
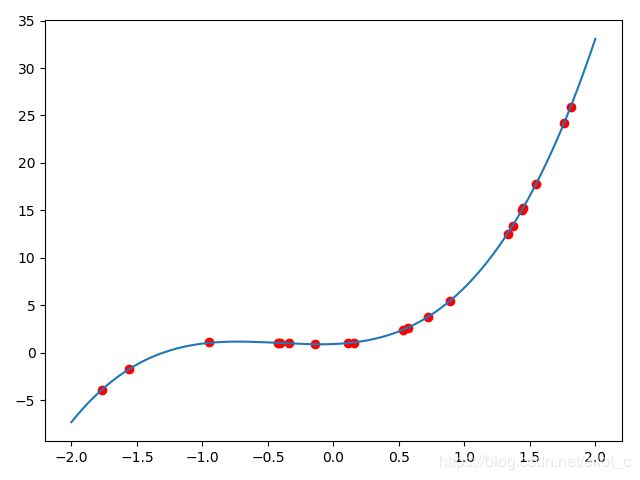
plt.show()

predicted function : y = 2.41 * x^3 + 2.98 * x^2 + 0.48 * x^1 + 0.95
real      function : y = 2.40 * x^3 + 3.00 * x^2 + 0.50 * x^1 + 0.90
torch.Size([20, 3])
torch.Size([4000, 3])

参考: 深度学习入门之PyTorch(廖星宇)

          https://www.jianshu.com/p/dda6846e8354