【密码学】ECC椭圆曲线加密
本篇文章介绍密码学中的一个概念:ECC加密算法。接下来我将从以下几个方面介绍一下ECC:
- 阿贝尔群(Abelian Group)
- 什么是椭圆曲线
- 有限域椭圆曲线计算
- 椭圆曲线加密(ECC)
- ECC参数选取
- ECC与比特币
椭圆曲线加密,全称EllipseCurve Cryptography,简称ECC。与传统的基于大素数因数分解难题的方式不同,ECC通过椭圆曲线的方式产生密钥。在ECC之前,有必要先介绍一下阿贝尔群的基本概念。
阿贝尔群(Abelian Group)
给定集合 G G 和操作 ⋅ ⋅ ,如果满足以下性质,则是 {G,⋅} { G , ⋅ } 群
- 封闭性
∀a,b∈G,a⋅b∈G ∀ a , b ∈ G , a ⋅ b ∈ G - 结合性
∀a,b,c∈G,(a⋅b)⋅c=a⋅(b⋅c) ∀ a , b , c ∈ G , ( a ⋅ b ) ⋅ c = a ⋅ ( b ⋅ c ) - 单位元
∃e∈G,∀a∈G,e⋅a=a⋅e=a ∃ e ∈ G , ∀ a ∈ G , e ⋅ a = a ⋅ e = a - 逆元
∀a∈G,∃a−1∈G,a⋅a−1=a−1⋅a=e ∀ a ∈ G , ∃ a − 1 ∈ G , a ⋅ a − 1 = a − 1 ⋅ a = e
在群的基础上,如果还满足交换性,那么这个群就是一个阿贝尔群了,通常我们也称作交换群。 - 交换性
∀a,b∈G,a⋅b=b⋅a ∀ a , b ∈ G , a ⋅ b = b ⋅ a
我们平时生活中所接触到的加法就是实数域上的阿贝尔群了,单位元是 0 0 ,乘法也是阿贝尔群,其单位元为 1 1 。
什么是椭圆曲线
我们来看下椭圆曲线的定义,椭圆曲线是在射影平面上满足维尔斯特方程 (Weierstrass)的所有点的集合,这句比较废话,不需要理解。其需要满足两点:
- 椭圆曲线关于x轴对称
- 平面中的一条直线和椭圆曲线相交,最多有三个交点
满足ECC的椭圆曲线有着如下形式:
一条椭圆曲线大概长这样:
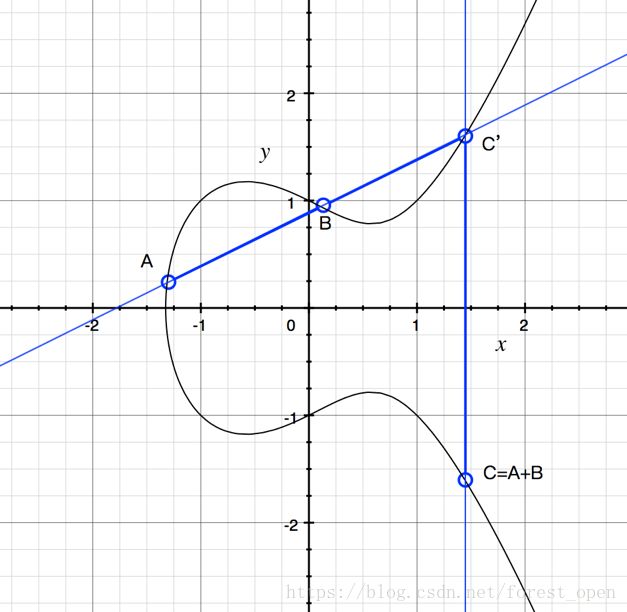
那么椭圆曲线如何去进行运算呢?不妨将椭圆曲线上面的运算定义为“+”运算,以上图为例,给定点A和点B,C’点为AB延长线与曲线的交点,做其对称点C,那么A+B=C。
那么如何计算A+A呢,这里用到极限的概念,做点A的切线就可以了,下图中A+A=C。
在这个定义之下,那么单位元是什么呢?实际上,单位元是一个理想的“无穷远点”(可以把这个点想象成点 (0,∞) ( 0 , ∞ ) 。这样,在椭圆曲线上面定义的 + + 运算就满足交换群的性质了。我们一步步看是否满足所有的交换群的性质呢?
- 封闭性:显然满足
- 结合性:自行理解
- 单位元: 0 0 ,因为 0 0 是无穷远点,因此 A A 和 0 0 的交点为 A A 的对称点,根据 + + 操作的计算规则, A+0=A A + 0 = A
- 逆元: A A 的逆元为 A A 关于 x x 轴的对称点
- 交换性:根据刚刚介绍的计算规则,显然有: A+B=B+A A + B = B + A
所以,我们定义在椭圆曲线上的运算实际上是一个交换群。
在定义了 + + 运算之后,我们还可以定义椭圆曲线上的乘法运算,按照递归的方式,可以有如下定义
比如给定一条椭圆曲线和A,我们可以按照以下过程求 3A 3 A :
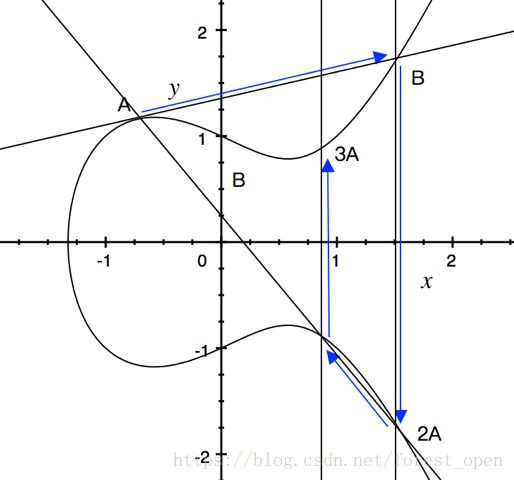
在定义了加法操作和乘法操作的基础之上,我们就可以知道为什么椭圆曲线可以用来加密了。我们知道,密码学中用来加密的方案通常都有一定的数学保证,那么椭圆曲线算法的保证是什么呢?
椭圆曲线的数学保障:已知椭圆曲线E,给定基点G和点kG,其中k为整数,无法在有效时间内计算出k。
上面给出了椭圆曲线的数学保障,如果不是很理解这个保障,那么我们可以对应着RSA的数学保障来理解一下这个问题,在指数运算之中,给定 a a 和 b b ,我们可以很快地计算出 ab a b ,但是给定 a a 和 ab a b ,却没有很快的计算方法计算出 b b (在取模的情况下)。这个说法仅仅助于理解,若想深入了解还需要从理论上给出一定的答复才严谨。
有限域椭圆曲线的运算
上面所提到的椭圆曲线的计算并不能直接用于密码学之中,因为在实数域上椭圆曲线的计算是有误差的,密码学要求精确。
在ECC中,我们还可以定义“阶”的概念,理解阶的概念可以类比于次方操作中阶的概念。对于圆锥曲线上一点 P P ,其阶为最小整数 a a ,使得 aP=0(modp) a P = 0 ( mod p ) ,其中 0 0 为单位元。
细心的读者可能会关心这样一个问题, 0 0 是假想的一个无穷远点,怎么算出这样一个 a a 呢。这时候就需要用到单位元的概念了。如果我们计算得到了 mP=P(modp) m P = P ( mod p ) ,那我们就知道 a=m−1 a = m − 1 。
上面所说的运算方法都是从几何角度给出的一个理解,那么如何在代数上进行计算呢?一般来说,给定,以下三步就可以计算:
(1)结果
(2)若 A=B A = B ,则
(3)若 A≠B A ≠ B
上述三个步骤其实就是先计算出直线,然后求直线和椭圆曲线的交点。如果还没有完全理解其中的过程可以参看这个网页的计算案例:https://www.cnblogs.com/Kalafinaian/p/7392505.html
那么为什么 A= A = B的时候斜率k是这么计算的呢,因为:
椭圆曲线加密(ECC)
上面介绍了ECC的计算过程,那么ECC是如何用来加密的呢?利用ECC进行加密首先需要给出 p,a,b,G,n p , a , b , G , n 。其中 p p 通常选取一个很大的素数以防止穷举, a a 和 b b 是椭圆曲线的参数, G G 为给定的椭圆曲线上的点, n n 为 G G 的阶。椭圆曲线加密正是利用了前面所说的给定自然数 m m 计算 mG m G 很容易而给定 mG m G 的结果无法很快计算 m m 这一个性质。下面给出一个ECC保密通信的算法:
- Alice选定曲线 E(p,a,b) E ( p , a , b ) ,并在上面取一点 G G 作为基点,同时计算 G G 的阶。比如选取 E(29,4,20),G(13,23) E ( 29 , 4 , 20 ) , G ( 13 , 23 ) ,则 G G 的阶为 37 37
- Alice选取一个常数 k k 作为私钥,并计算出 kG k G 作为公钥。比如选取 k=25 k = 25 ,则 kG=25G=(14,6) k G = 25 G = ( 14 , 6 )
- Alice公开 E(29,4,20),K(14,6),G(13,23) E ( 29 , 4 , 20 ) , K ( 14 , 6 ) , G ( 13 , 23 )
- Bob接收消息之后首先将信息编码到点 M M ,并产生一个随机整数 r(r<n) r ( r < n ) 。假设 r=6 r = 6 ,需要加密的信息为 3 3 则计算 y2=33+4×3+20(modp) y 2 = 3 3 + 4 × 3 + 20 ( mod p ) 。因此 y=28 y = 28 ,所以点 M(3,28) M ( 3 , 28 )
- Bob计算 C1=M+rK;C2=rG C 1 = M + r K ; C 2 = r G 并发送给Alice
- Alice计算 C1−kC2 C 1 − k C 2 即可解密Bob发来的消息
为什么Alice可以解密呢,因为
通过这个过程,相比大家应该大致理解了ECC的设计思路了。
ECC参数选取
学术上通常将一条椭圆曲线定义为 T=(p,a,b,G,n,h) T = ( p , a , b , G , n , h ) ,其中 p p 为大素数, a,b a , b 确定一条椭圆曲线的表达式, G G 为基点, n n 为 G G 的阶, h h 是椭圆曲线上所有点的个数 m m 与 n n 相除的商的整数部分。参数的选择一般如下,可以参考:
(https://www.cnblogs.com/Kalafinaian/p/7392505.html )
- p p 越大越好,但是 p p 越大,运算速度会受到影响。 200 200 bit 即可满足一般的安全需求
- n n 应该为素数(需要数论知识加以理解)
- h≤4;p≠n×h;pt≠1(modp)(1≤t<20) h ≤ 4 ; p ≠ n × h ; p t ≠ 1 ( mod p ) ( 1 ≤ t < 20 )
- 4a3+27b2≠0(modp) 4 a 3 + 27 b 2 ≠ 0 ( mod p )
ECC和RSA相比,提供的安全等级更高(虽然我不知道为什么),160位ECC既可以与1024位RSA,DSA拥有相同的安全强度,同时处理速度更快,因此在存储和传输时候对空间的要求更低,当然,ECC的设计难度和RSA相比也难更多。
ECC与比特币
由于比特币技术的火热,ECC技术也更广为人知了。比特币中使用了Secp256k1,其参数在https://en.bitcoin.it/wiki/Secp256k1 中有详细介绍。
结束
本篇内容到这里就结束了,若想知道更多和信息安全有关的技术可在公众号留言哦。识别以下二维码可以成文本公众号的小粉丝,关注更多和差分隐私有关的前沿技术哦。