莫队算法入门 BZOJ 2038

目前的题型概括为三种：普通莫队，树形莫队以及带修莫队。

下面介绍普通莫队算法：

普通莫队算法是一种离线算法，不带修改 操作。其通过对询问操作的执行顺序进行更改，然后使用最暴力的方法，可以达到很好的复杂度。

首先,如果要用莫队算法，则必须满足已知ans[l,r]可以得到ans[l,r+1]，ans[l,r-1],ans[l+1,r],ans[l-1,r]

莫队算法的实现步骤为： 

1、先对原序列进行分块。(sqrt(n)块) 

2、离线操作，对询问进行排序，以左端点所在块编号 为第一关键字，右端点的位置为第二关键字，进行排序。然后维护[l,r]的答案，并不断调整[l,r] 使其于查询区间相等

典型例题：BZOJ2038

2038: [2009国家集训队]小Z的袜子(hose)

Time Limit: 20 Sec   Memory Limit: 259 MB
Submit: 13738   Solved: 6223
[ Submit][ Status][ Discuss]

Description

作为一个生活散漫的人，小Z每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿。终于有一天，小Z再也无法忍受这恼人的找袜子过程，于是他决定听天由命……
具体来说，小Z把这N只袜子从1到N编号，然后从编号L到R(L 尽管小Z并不在意两只袜子是不是完整的一双，甚至不在意两只袜子是否一左一右，他却很在意袜子的颜色，毕竟穿两只不同色的袜子会很尴尬。
你的任务便是告诉小Z，他有多大的概率抽到两只颜色相同的袜子。当然，小Z希望这个概率尽量高，所以他可能会询问多个(L,R)以方便自己选择。

Input

输入文件第一行包含两个正整数N和M。N为袜子的数量，M为小Z所提的询问的数量。接下来一行包含N个正整数Ci，其中Ci表示第i只袜子的颜色，相同的颜色用相同的数字表示。再接下来M行，每行两个正整数L，R表示一个询问。

Output

包含M行，对于每个询问在一行中输出分数A/B表示从该询问的区间[L,R]中随机抽出两只袜子颜色相同的概率。若该概率为0则输出0/1，否则输出的A/B必须为最简分数。（详见样例）

Sample Input

6 4
1 2 3 3 3 2
2 6
1 3
3 5
1 6

Sample Output

2/5
0/1
1/1
4/15
【样例解释】
询问1：共C(5,2)=10种可能，其中抽出两个2有1种可能，抽出两个3有3种可能，概率为(1+3)/10=4/10=2/5。
询问2：共C(3,2)=3种可能，无法抽到颜色相同的袜子，概率为0/3=0/1。
询问3：共C(3,2)=3种可能，均为抽出两个3，概率为3/3=1/1。
注：上述C(a, b)表示组合数，组合数C(a, b)等价于在a个不同的物品中选取b个的选取方案数。
【数据规模和约定】
30%的数据中 N,M ≤ 5000；
60%的数据中 N,M ≤ 25000；
100%的数据中 N,M ≤ 50000，1 ≤ L < R ≤ N，Ci ≤ N。

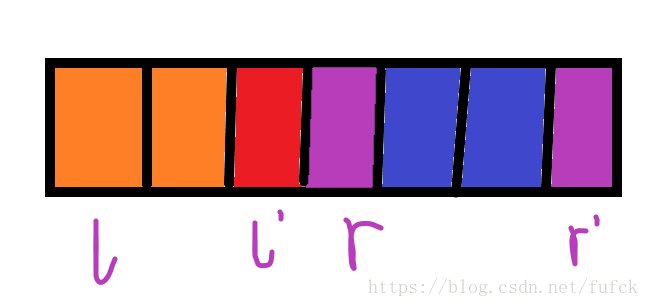
如果我们知道了[l,r] 的答案，如何快速求得[l',r']的答案。

分母为（r'-l'+1）*(r'-l')

分子为 （A1*A1+A2*A2+...-(r'-l'+1)） {Ax表示颜色为x的袜子数，前半部分表示选两次袜子颜色数相同的个数，后半部分表示选到两只相同袜子的情况}

Ax可以O（abs（l-l'）+abs(r-r')） 推得。

#include 
#include
#include
#include
#include
#include
#define go(i,a,b) for(int i=a;i<=b;i++)
#define mem(a,b)  memset(a,b,sizeof(a))
#define ll long long
const int N=50010;
using namespace std;
struct Mo{int l,r,ID;ll A,B;}q[N];
ll S(ll x) {return x*x;}
ll GCD(ll a,ll b) {while(b^=a^=b^=a%=b);return a;}
int n,m,col[N],unit,Be[N];
ll sum[N],ans;
bool cmp(Mo a,Mo b){return Be[a.l]==Be[b.l]?a.rq[i].l) revise(l-1,1),l--;
	  	while(rq[i].r) revise(r,-1),r--;
	  	if(q[i].l==q[i].r){q[i].A=0;q[i].B=1;continue;}
	  	q[i].A=ans-(q[i].r-q[i].l+1);
	  	q[i].B=1LL*(q[i].r-q[i].l+1)*(q[i].r-q[i].l);
	  	ll gcd=GCD(q[i].A,q[i].B);
	  	q[i].A/=gcd;q[i].B/=gcd;
	  }
	sort(q+1,q+1+m,CMP);
	go(i,1,m) printf("%lld/%lld\n",q[i].A,q[i].B);
	return 0;
}