PyTorch学习笔记(15) ——PyTorch中的contiguous

本文转载自栩风在知乎上的文章《PyTorch中的contiguous》。我觉得很好，特此转载。

0. 前言

本文讲解了pytorch中contiguous的含义、定义、实现，以及contiguous存在的原因，非contiguous时的解决办法。并对比了numpy中的contiguous。

---

contiguous 本身是形容词，表示连续的，关于 contiguous，PyTorch 提供了is_contiguous、contiguous(形容词动用)两个方法 ，分别用于判定Tensor是否是 contiguous 的，以及保证Tensor是contiguous的。

1.PyTorch中的is_contiguous是什么含义？

is_contiguous直观的解释: Tensor底层一维数组元素的存储顺序与Tensor按行优先一维展开的元素顺序是否一致。

Tensor多维数组底层实现是使用一块连续内存的1维数组（行优先顺序存储，下文描述），Tensor在元信息里保存了多维数组的形状，在访问元素时，通过多维度索引转化成1维数组相对于数组起始位置的偏移量即可找到对应的数据。某些Tensor操作（如transpose、permute、narrow、expand）与原Tensor是共享内存中的数据，不会改变底层数组的存储，但原来在语义上相邻、内存里也相邻的元素在执行这样的操作后，在语义上相邻，但在内存不相邻，即不连续了（is not contiguous）。

如果想要变得连续使用contiguous方法，如果Tensor不是连续的，则会重新开辟一块内存空间保证数据是在内存中是连续的，如果Tensor是连续的，则contiguous无操作。

1.1 行优先

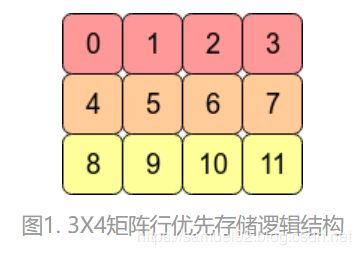
行是指多维数组一维展开的方式，对应的是列优先。C/C++中使用的是行优先方式（row major），Matlab、Fortran使用的是列优先方式（column major），PyTorch中Tensor底层实现是C，也是使用行优先顺序。举例说明如下：

>>> t = torch.arange(12).reshape(3,4)
>>> t
tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]])

二维数组 t 如图1：

数组 t 在内存中实际以一维数组形式存储，通过flatten方法查看 t 的一维展开形式，实际存储形式与一维展开一致，如图2，

>>> t.flatten()
tensor([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

说明：图1、图2来自：What is the difference between contiguous and non-contiguous arrays? 图1、图2 中颜色相同的数据表示在同一行，不论是行优先顺序、或是列优先顺序，如果要访问矩阵中的下一个元素都是通过偏移来实现，这个偏移量称为步长(stride[1])。在行优先的存储方式下，访问行中相邻元素物理结构需要偏移1个位置，在列优先存储方式下偏移3个位置。

2. 为什么需要 contiguous ？

• torch.view等方法操作需要连续的Tensor。

transpose、permute 操作虽然没有修改底层一维数组，但是新建了一份Tensor元信息，并在新的元信息中的 重新指定 stride。torch.view 方法约定了不修改数组本身，只是使用新的形状查看数据。如果我们在 transpose、permute 操作后执行 view，Pytorch 会抛出以下错误：

invalid argument 2: view size is not compatible with input tensor's size and stride (at least one dimension 
spans across two contiguous subspaces). Call .contiguous() before .view(). 
at /Users/soumith/b101_2/2019_02_08/wheel_build_dirs/wheel_3.6/pytorch/aten/src/TH/generic/THTensor.cpp:213

为什么 view 方法要求Tensor是连续的？考虑以下操作，

>>>t = torch.arange(12).reshape(3,4)
>>>t
tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]])
>>>t.stride()
(4, 1)
>>>t2 = t.transpose(0,1)
>>>t2
tensor([[ 0,  4,  8],
        [ 1,  5,  9],
        [ 2,  6, 10],
        [ 3,  7, 11]])
>>>t2.stride()
(1, 4)
>>>t.data_ptr() == t2.data_ptr() # 底层数据是同一个一维数组
True
>>>t.is_contiguous(),t2.is_contiguous() # t连续，t2不连续
(True, False)

t2 与 t 引用同一份底层数据 a: [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11], t2和t两者仅是stride、shape不同。如果执行 t2.view(-1)，期望返回b（但实际会报错）[ 0, 4, 8, 1, 5, 9, 2, 6, 10, 3, 7, 11]

可以看出，在 a 的基础上使用一个新的 stride 无法直接得到 b ，需要先使用 t2 的 stride (1, 4) 转换到 t2 的结构，再基于 t2 的结构使用 stride (1,) 转换为形状为 (12,)的 b 。但这不是view工作的方式，view仅在底层数组上使用指定的形状进行变形，即使 view 不报错，它返回的数据是 [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11], 而对t2而言，显然我们的目标是获取[ 0, 4, 8, 1, 5, 9, 2, 6, 10, 3, 7, 11]， 那么，如果我们想得到后者，该怎么办呢？

>>>t3 = t2.contiguous()
>>>t3
tensor([[ 0,  4,  8],
        [ 1,  5,  9],
        [ 2,  6, 10],
        [ 3,  7, 11]])
>>>t3.data_ptr() == t2.data_ptr() # 底层数据不是同一个一维数组
False

可以看到，我们用t3 = t2.contiguous()即可， 开辟了一块新的内存空间给t3，也就是说：t与t2 底层数据指针一致，t3 与 t2 底层数据指针不一致，说明确实重新开辟了内存空间。

3. 为什么不在view 方法中默认调用contiguous方法?

• ① 历史原因
  因为历史上view方法已经约定了共享底层数据内存，返回的Tensor底层数据不会使用新的内存，如果在view中调用了contiguous方法，则可能在返回Tensor底层数据中使用了新的内存，这样打破了之前的约定，破坏了对之前的代码兼容性。为了解决用户使用便捷性问题，PyTorch在0.4版本以后提供了reshape方法，实现了类似于 tensor.contigous().view(*args)的功能，如果不关心底层数据是否使用了新的内存，则使用reshape方法更方便。 [3]

• ② 出于性能考虑(保证Tensor语义顺序和逻辑顺序的一致性)

对连续的Tensor来说，语义上相邻的元素，在内存中也是连续的，访问相邻元素是矩阵运算中经常用到的操作，语义和内存顺序的一致性是缓存友好的（What is a “cache-friendly” code?[4]），在内存中连续的数据可以（但不一定）被高速缓存预取，以提升CPU获取操作数据的速度。transpose、permute 后使用 contiguous 方法则会重新开辟一块内存空间保证数据是在逻辑顺序和内存中是一致的，连续内存布局减少了CPU对对内存的请求次数（访问内存比访问寄存器慢100倍[5]），相当于空间换时间。

4. PyTorch中判读张量是否连续的实现

PyTorch中通过调用 is_contiguous 方法判断 tensor 是否连续，底层实现为 TH 库中THTensor.isContiguous 方法：

int THTensor_(isContiguous)(const THTensor *self)
{
  long z = 1;
  int d;
  for(d = self->nDimension-1; d >= 0; d--)
  {
    if(self->size[d] != 1)
    {
      if(self->stride[d] == z)
        z *= self->size[d];
      else
        return 0;
    }
  }
  return 1;
}

为方便加上一些调试信息，翻译为 Python 代码如下：

def isContiguous(tensor):
    """
    判断tensor是否连续    
    :param torch.Tensor tensor: 
    :return: bool
    """

    z = 1
    d = tensor.dim() - 1
    size = tensor.size()
    stride = tensor.stride()
    print("stride={} size={}".format(stride, size))
    while d >= 0:
        if size[d] != 1:
            if stride[d] == z:
                print("dim {} stride is {}, next stride should be {} x {}".format(d, stride[d], z, size[d]))
                z *= size[d]                
            else:
                print("dim {} is not contiguous. stride is {}, but expected {}".format(d, stride[d], z))
                return False
        d -= 1
    return True

判定上文中 t、t2 是否连续的输出如下：

>>>isContiguous(t)
stride=(4, 1) size=torch.Size([3, 4])
dim 1 stride is 1, next stride should be 1 x 4
dim 0 stride is 4, next stride should be 4 x 3

True
>>>isContiguous(t2)
stride=(1, 4) size=torch.Size([4, 3])
dim 1 is not contiguous. stride is 4, but expected 1

False

从isContiguous 实现可以看出，最后1维的 stride 必须为z = 1（逻辑步长），这是合理的，最后1维即逻辑结构上最内层数组，其相邻元素间隔位数为1，按行优先顺序排列时，最内层数组相邻元素间隔应该为1。

参考资料

[3] view() after transpose() raises non contiguous error #764
[4] What is a “cache-friendly” code?
[5] 计算机缓存Cache以及Cache Line详解