PriorityQueue的BinaryHeap实现

PriorityQueue（优先队列）有很多应用场景，例如去听一场音乐会，假如票已经都卖完了，但是还有许多没票的人在排队等是否有人退票，如果有人退票，那么系统就需要把这张票分类给优先级最高的那个排队者（这里的优先级可以是排队的时间，或者交的钱多少等，这里的优先级条件对应priorityqueue中的key）。

PriorityQueue的实现方法有多种，包括SortedList，UnSortedList以及BinaryHeap。其核心操作为insert()与removeMin()，BinaryHeap看似实现比其他两种复杂，但是在这两种核心操作的效率上却优于另外两个。

下面介绍一下BinaryHeap，BinaryHeap就是一种特殊的complete binary tree（完全二叉树），它的每个节点的key值要大于它的父亲节点。所以最小的节点永远是根节点。又由于它是一棵完全二叉树，因此用一维数组来实现。数组的下标能够映射出节点间的父子关系，其中节点i的父节点的下标为floor(i / 2), i的左右孩子节点分别为2i与2i+1。为了映射出这种关系，在实现一维数组的时候数组的第一个元素为空，因为下标0将打破这种映射关系。元素按层次遍历顺序存储在数组中，如下图的一个BinaryHeap的存储：

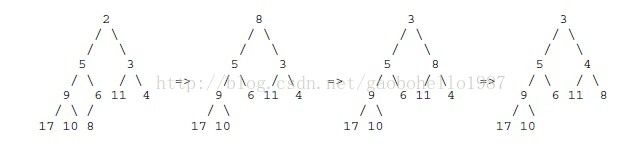
对于核心操作removeMin()，因为根节点是最小的节点，因此每次都是remove根节点，根节点remove后我们把二叉树的最后一个叶子节点（上图的节点8）放在根节点的位置，放完后为了保持前面提到的二叉树的节点顺序属性，我们将该跟节点与它的左右孩子节点比较，如果它大于其中任何一个或者两个，将它与最小的那个做位置交换，然后继续该比较，直到该节点找到它的合适位置（小于它的子节点或者已经是叶子节点），这样操作后二叉树又保持了原有的属性。如下图：

对于核心操作insert(),现将插入的节点插入到树的最后一个叶子节点后发，也就是数组的最后一个元素后面（这里涉及到数组已满重新分配数组的问题），然后将该节点与它的父亲节点比较，如果它小于父亲节点，则将它与父亲节点对换位置，执行此操作直到它大于父亲节点或者已经到达根节点。如下图：

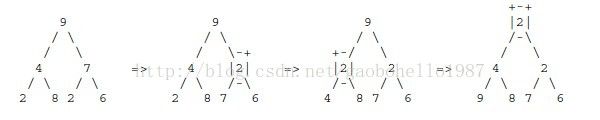
另外一个重要操作是给出一些数后怎么构造一个BinaryHeap，一个直接方法是按照上述方法一个一个把节点插入进去，但是这种方法的复杂度为O（nlgn），可以用下边这个复杂度为Theta(n)。这种方法是先将这些数扔进实现BinaryHeap的数组，也就是组成一颗不是BinaryHeap的完全二叉树，然后找到这棵树的最后一个非叶子节点，然后对这个节点采用与remove()中类似的方法找到该节点的合适位置，完成后继续对该节点原来位置的前一个节点进行该操作。如下图：

这种BirnaryHeap在insert()与removeMin()操作与其他两种实现方法（SortedList与UnSortedList)的比较如下图：

具体实现代码：

PriorityQueue接口：

public interface PriorityQueue {
	public int size();
	public boolean isEmpty();
	Entry insert(int key, Object value);
	Entry min();
	Entry removeMin();
}

Entry类：

public class Entry {
	int key;
	Object value;
	public Entry(int key, Object value){
		this.key = key;
		this.value = value;
	}
}

BinaryHeap类：

public class BinaryHeap implements PriorityQueue{
	
	Entry[] entries;
	public BinaryHeap(int i){
		Random rand = new Random();
		rand.setSeed(System.currentTimeMillis());
		entries = new Entry[2 * (i + 1)];
		for(int j = 0; j < i; j++){
			int key = rand.nextInt(1000);
			Object value = "value is:" + key;
			entries[j + 1] = new Entry(key,value);
		}
		int bubbleIndx =  (int) Math.floor(i / 2);
		while(bubbleIndx > 0){
			downSwap(bubbleIndx);
			bubbleIndx--;
		}
		
	}

	private void downSwap(int bubbleIndx) {
		while(bubbleIndx * 2 <= this.size() || bubbleIndx * 2 + 1 <= this.size()){
			int leftChildIndx = bubbleIndx * 2;
			int rightChildIndx = bubbleIndx * 2 + 1;
			Entry temp = entries[bubbleIndx];
			if(entries[rightChildIndx] != null){
				if(entries[bubbleIndx].key > entries[leftChildIndx].key || 
					entries[bubbleIndx].key > entries[rightChildIndx].key){
					if(entries[leftChildIndx].key <= entries[rightChildIndx].key){
						entries[bubbleIndx] = entries[leftChildIndx];
						entries[leftChildIndx] = temp;
						bubbleIndx = leftChildIndx;
					}else{
						entries[bubbleIndx] = entries[rightChildIndx];
						entries[rightChildIndx] = temp;
						bubbleIndx = rightChildIndx;
					}
				}else{
					break;
				}
			}else{
				if(entries[bubbleIndx].key > entries[leftChildIndx].key){
					entries[bubbleIndx] = entries[leftChildIndx];
					entries[leftChildIndx] = temp;
				}
//				bubbleIndx = leftChildIndx;
				break;
			}
			
		}
	}

	@Override
	public int size() {
		int size = 0;
		int index = 1;
		while(index < entries.length && entries[index] != null){
			size++;
			index++;
		}
		return size;
	}

	@Override
	public boolean isEmpty() {
		return entries[1] == null;
	}

	@Override
	public Entry insert(int key, Object value) {
		Entry insertEntry = new Entry(key, value);
		if(this.size() == this.entries.length - 1){
			Entry[] oldEntries = this.entries;
			this.entries = new Entry[entries.length * 2];
			for(int i = 1; i < oldEntries.length; i++){
				entries[i] = oldEntries[i];
			}
		}
		entries[this.size() + 1] = insertEntry;
		int bubbleIndx = this.size();
		swapUp(bubbleIndx);
		return insertEntry;
	}

	private void swapUp(int bubbleIndx) {
		while(bubbleIndx > 1 && entries[bubbleIndx].key < entries[(int) Math.floor(bubbleIndx / 2)].key){
			int parentIndx = (int) Math.floor(bubbleIndx / 2);
			Entry temp = entries[bubbleIndx];
			entries[bubbleIndx] = entries[parentIndx];
			entries[parentIndx] = temp;
			bubbleIndx = parentIndx;
		}
		
	}

	@Override
	public Entry min() {
		return entries[1];
	}

	@Override
	public Entry removeMin() {
		if(this.isEmpty()){
			return null;
		}
		Entry minEntry = this.min();
		entries[1] = entries[this.size()];
		entries[this.size()] = null;
		downSwap(1);
		return minEntry;
	}
	
	

}

测试类：

public class Test {
	public static void main(String[] args){
		BinaryHeap bHeap = new BinaryHeap(10);
		for(int i = 1; i <= bHeap.size(); i++){
			System.out.print(bHeap.entries[i].key + ",");
		}
		System.out.println("The size is:" + bHeap.size());
		bHeap.removeMin();
		for(int i = 1; i <= bHeap.size(); i++){
			System.out.print(bHeap.entries[i].key + ",");
		}
		System.out.println("The size is:" + bHeap.size());
		bHeap.insert(2900, "this is the largest");
		bHeap.insert(1, "this is the smallest");
		bHeap.insert(1, "this is the smallest");
		bHeap.insert(1, "this is the smallest");
		for(int i = 1; i <= bHeap.size(); i++){
			System.out.print(bHeap.entries[i].key + ",");
		}
		System.out.println("The size is:" + bHeap.size());
	}
}