**图结构练习——最短路径**

图结构练习——最短路径
Time Limit: 1000 ms Memory Limit: 65536 KiB

Problem Description
给定一个带权无向图，求节点1到节点n的最短路径。

Input
输入包含多组数据，格式如下。
第一行包括两个整数n m，代表节点个数和边的个数。(n<=100)
剩下m行每行3个正整数a b c，代表节点a和节点b之间有一条边，权值为c。

Output
每组输出占一行，仅输出从1到n的最短路径权值。（保证最短路径存在）

Sample Input
3 2
1 2 1
1 3 1
1 0
Sample Output
1
0
Hint

Source
赵利强
查看原代码 请点击 小銍2016年06月09日 13:29:09

代码一：
Floyd算法

#include 
#define inf 0x3f3f3f3f
using namespace std;

int e[10010][10010];//邻接矩阵
// 最短路之Floyd算法
int main()
{
    int n, m;
    while(cin >> n >> m)
    {
        for( int i = 1; i <= n; i++)
        {
            for( int j = 1; j <= n; j++)
            {
                (i == j) ? e[i][j] = 0 : e[i][j] = inf;
            }
        }
        while( m-- )
        {
            int u, v, w;
            cin >> u >> v >> w;
            if(e[u][v] > w)
                e[u][v] = e[v][u] = w;
        }
      /*  最开始只允许经过1号顶点进行中转，
        接下来只允许经过1和2号顶点进行中转...
        允许经过1~n号所有顶点进行中转，
        求任意两点之间的最短路程。*/
        for(int k = 1; k <= n; k++)
        {
            for(int i = 1; i <= n; i++)
            {
                  if( e[i][k]!= inf)
                  {
                      for( int j = 1; j <= n; j++)
                      {
                          e[i][j] = min(e[i][k] + e[k][j], e[i][j]);
                      }
                  }
            }
        }
        cout << e[1][n] << endl;
    }
    return 0;
}

代码二：
Bellman_Ford算法（1）

#include 
#define inf 0x3f3f3f3f
using namespace std;

struct edge
{
    int u, v, w; // w >0;

}Edge[101000];

int n, m;
int dis[101];

void Bellman_Ford(int st)
{
    for( int i = 1; i <= n; i++)   //第一，初始化所有点。每一个点保存一个值，
    {
        dis[i] = inf;             //表示从原点到达这个点的距离，将原点的值设为0， 
    }
    dis[st] = 0;   //其它的点的值设为无穷大（表示不可达）。
    for( int k = 2; k <= n; k++) // 第二，进行循环，循环下标为从
    //1到n－1（n等于图中点的个数）(2--->n)。
    {
        for( int i = 1; i <= 2 * m; i++) //在循环内部，遍历所有的边，进行松弛计算。
        {
            if(dis[Edge[i].u] != inf && dis[Edge[i].v] > dis[Edge[i].u] + Edge[i].w)
            {
                dis[Edge[i].v] = dis[Edge[i].u] + Edge[i].w;
            }
        }
    }
    /*第三，遍历途中所有的边（edge（u，v）），判断是否存在这样情况：
d（v） > d (u) + w(u,v)
则返回false，表示途中存在从源点可达的权为负的回路。*/
    cout << dis[n] << endl;
}
int main()
{
    while(cin >> n >> m)
    {
        memset(Edge, inf, sizeof(Edge));
        for(int i = 1; i <= m; i++)
        {
            int u, v, w;
            cin >> u >> v >> w;
            Edge[i].u = u; Edge[i].v = v; Edge[i].w = w;
            Edge[i + m].u = v; Edge[i + m].v = u; Edge[i + m].w = w;//
        }
        Bellman_Ford(1);
    }
    return 0;
}

查看原文请点击 bellman-ford详解（转载）

Dijkstra算法是处理单源最短路径的有效算法，但它局限于边的权值非负的情况，若图中出现权值为负的边，Dijkstra算法就会失效，求出的最短路径就可能是错的。这时候，就需要使用其他的算法来求解最短路径，Bellman-Ford算法就是其中最常用的一个。该算法由美国数学家理查德•贝尔曼（Richard Bellman, 动态规划的提出者）和小莱斯特•福特（Lester Ford）发明。Bellman-Ford算法的流程如下：
给定图G(V, E)（其中V、E分别为图G的顶点集与边集），源点s，
数组Distant[i]记录从源点s到顶点i的路径长度，初始化数组Distant[n]为, Distant[s]为0；

以下操作循环执行至多n-1次，n为顶点数：
对于每一条边e(u, v)，如果Distant[u] + w(u, v) < Distant[v]，则另Distant[v] = Distant[u]+w(u, v)。w(u, v)为边e(u,v)的权值；
若上述操作没有对Distant进行更新，说明最短路径已经查找完毕，或者部分点不可达，跳出循环。否则执行下次循环；
为了检测图中是否存在负环路，即权值之和小于0的环路。对于每一条边e(u, v)，如果存在Distant[u] + w(u, v) < Distant[v]的边，则图中存在负环路，即是说改图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。
可知，Bellman-Ford算法寻找单源最短路径的时间复杂度为O(V*E).

首先介绍一下松弛计算。如下图：

Bellman－Ford算法可以大致分为三个部分
第一，初始化所有点。每一个点保存一个值，表示从原点到达这个点的距离，将原点的值设为0，其它的点的值设为无穷大（表示不可达）。
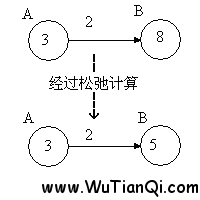
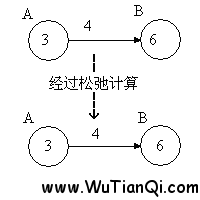
第二，进行循环，循环下标为从1到n－1（n等于图中点的个数）。在循环内部，遍历所有的边，进行松弛计算。
第三，遍历途中所有的边（edge（u，v）），判断是否存在这样情况：
d（v） > d (u) + w(u,v)
则返回false，表示途中存在从源点可达的权为负的回路。

之所以需要第三部分的原因，是因为，如果存在从源点可达的权为负的回路。则 应为无法收敛而导致不能求出最短路径。
代码二：
Bellman_Ford算法（2）下面代码为博主乱改hhh

#include 
#define inf 0x3f3f3f3f
using namespace std;

struct edge
{
    int u, v, w; // w >0;现 假设 w权值存在小鱼0 的情况；

}Edge[101000];

int n, m;
int dis[101]; // 结点到源点最小距离
 bool flag = 1;
int Bellman_Ford(int st)
{
    for( int i = 1; i <= n; i++)   //第一，初始化所有点。每一个点保存一个值，
    {
        dis[i] = inf;             //表示从原点到达这个点的距离，将原点的值设为0，
    }
    dis[st] = 0;   //其它的点的值设为无穷大（表示不可达）。
    for( int k = 2; k <= n; k++) // 第二，进行循环，循环下标为从1到n－1（n等于图中点的个数）(2--->n)。
    {
        for( int i = 1; i <= 2 * m; i++) //在循环内部，遍历所有的边，进行松弛计算。
        {
            if(dis[Edge[i].u] != inf && dis[Edge[i].v] > dis[Edge[i].u] + Edge[i].w)
            {
                dis[Edge[i].v] = dis[Edge[i].u] + Edge[i].w;
            }
        }
    }
    /*第三，遍历途中所有的边（edge（u，v）），判断是否存在这样情况：
d（v） > d (u) + w(u,v)
则返回false，表示途中存在从源点可达的权为负的回路。*/

       for( int i = 1; i < 2 * m; i++)
       if(dis[Edge[i].v] > dis[Edge[i].u] + Edge[i].w)
           {
               flag = 0;
               break;
           }
       return flag;
}
int main()
{
    while(cin >> n >> m)
    {
        memset(Edge, inf, sizeof(Edge));
        for(int i = 1; i <= m; i++)
        {
            int u, v, w;
            cin >> u >> v >> w;
            Edge[i].u = u; Edge[i].v = v; Edge[i].w = w;
            Edge[i + m].u = v; Edge[i + m].v = u; Edge[i + m].w = w;// 为无向图的 点与权值赋值
        }
        Bellman_Ford(1);
        if(flag == 1)
            cout << dis[n] << endl;
    }
    return 0;
}