【图像特征】【OPENCV】SIFT，SURF，ORB，Harris，FAST，量化匹配度

图像特征

本章主要介绍一些特征点的理论及opencv如何调用，如有疏漏望不吝赐教，对你如果有帮助，不胜荣幸。xue.2018.4.9

注： Opencv出现的特征点检测原理可以从如下链接了解
1、OpencvTutorial>>feature2d module.2D Features framework
2、OpencvTutorial>>OpenCV-Python Tutorial>>Feature Detection and Description

目录：

环境：
Win10.x64
VS2015
Opencv3.4

注： Opencv-contrib搭建参考连接

---

1.0 SIFT(Scale-invariant feature transform)

尺度缩放，旋转，亮度变化具有不变性
应用范围：物体识别，机器人地图感知与导航，影像缝合，3D模型建立，手势识别，影像追踪和动作对比。

1.1 参考文献

原理参考：
1，SIFT算法详解
2，SIFT特征提取分析
3. SIFT原理与源码分析：DoG尺度空间构造
4.Introduction to SIFT (Scale-Invariant Feature Transform)
5.sift

1.2 尺度空间和多分辨率

尺度空间：
 1，考虑图像在多尺度下的描述，获取感兴趣物体的最佳尺度。
 2，如果在多尺度下都可以检测出相同关键点，即具有尺度不变性。
 3，图像的尺度空间表达->就是图像在所有尺度下的描述。

尺度空间表达 采用高斯核
 1，高斯核实唯一可以产生多尺度空间的核。
 2，高斯卷积只是表现尺度空间的一种形式。

金字塔多分辨率
图像金字塔一般包含两个步骤：
 1，低通滤波器平滑图像
 2，对平滑图像进行降采样。

尺度空间表达是由不同高斯核平滑卷积得到，在所有尺度上有相同的分辨率
金字塔多分辨率表达每层分辨率减少固定比率

1.3 Scale-space Extrema Detection

 Log(Laplace of Gaussian) pyramid 代价高，SIFT采用了高斯差分(Difference of Gaussian)近似LOG。

注： 每个octave含有相同分辨率，不同高斯核 σ σ 和 kσ k σ 。

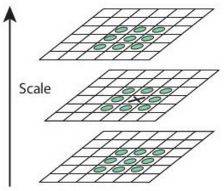
注： 建立DOG后，一个像素(上图中黑X)，同其周围8个像素点，和上下不同尺度9个像素点作对比，如果是局部极值，则说是当前尺度空间的特征点

不同的高斯尺度组

根据经验建议：octaves =4，number of scale levels =5, σ=1.6 σ = 1.6 , k=(√2) k = ( 2 )

1.4Keypoint Localization（精确化）

&emsp；1，移除弱极值点：当获取特征点后，需要对其进行提炼以获得更精确的结果（上述的极值点都是在离散空间进行搜索的）。通过泰勒公式对DOG进行展开，滤除极值小于contrastThresholdValue的情况。

原文中contrastThresholdValue =0.04

  2，删除边缘效应：DOG对边缘有较强的响应，落在边缘的点也不是稳定的特征点。通过2*2 hessian matrix计算主要轮廓。

其中令 α=λmax α = λ m a x , β=λmin β = λ m i n ;
Tr(H)=Dxx+Dyy=α+β T r ( H ) = D x x + D y y = α + β
Det(H)=DxxDyy−(Dyy)2=αβ D e t ( H ) = D x x D y y − ( D y y ) 2 = α β
令 γ=αβ γ = α β 则有：
Tr(H)2Det(H)=(α+β)2αβ=(γ+1)2γ T r ( H ) 2 D e t ( H ) = ( α + β ) 2 α β = ( γ + 1 ) 2 γ
通过 (γ+1)2γ ( γ + 1 ) 2 γ 比率大于一定值得特征点筛除。

原文中edgeThresholdValue =10

1.5 Orientation Assignment(方向赋值)

  关键点一定范围内图像像素对关键点方向产生的贡献。
对这个范围内(半径 r=3∗1.5α r = 3 ∗ 1.5 α )的图像进行 α α 的Gaussian平滑，梯度幅值，角度通过如下公式计算：
m(x,y)=(L(x+1,y)−L(x−1,y))2+(L(x,y+1)−L(x,y−1))2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√ m ( x , y ) = ( L ( x + 1 , y ) − L ( x − 1 , y ) ) 2 + ( L ( x , y + 1 ) − L ( x , y − 1 ) ) 2
θ(x,y)=arctan(L(x,y+1)−L(x,y−1)L(x+1,y),L(x−1,y)) θ ( x , y ) = a r c t a n ( L ( x , y + 1 ) − L ( x , y − 1 ) L ( x + 1 , y ) , L ( x − 1 , y ) )
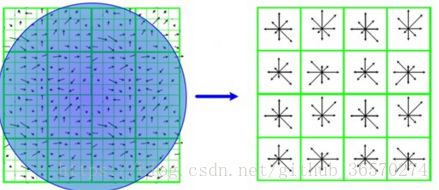
将角度分为8个分量，8个分量重叠加幅值，如下图所示：

峰值：主方向
峰值80%：辅方向，一个监测点可以检测到多个方向。

Lowe论文指出15%的关键点具有多方向
此时的关键点信息有 (x,y,σ,θ) ( x , y , σ , θ )

1.6 Keypoint Descriptor特征点描述

 Now keypoint descriptor is created. A 16x16 neighbourhood around the keypoint is taken. It is devided into 16 sub-blocks of 4x4 size. For each sub-block, 8 bin orientation histogram is created. So a total of 128 bin values are available. It is represented as a vector to form keypoint descriptor. In addition to this, several measures are taken to achieve robustness against illumination changes, rotation etc.
 为了消除光照变化影响，需要做归一化处理。

1.7Keypoint Matching

 对比通过两幅图像特征点周围像素点，但有时候匹配点第二优和第一差别不大，此时计算最近距离/第二距离的比率，如果大于0.8，则拒绝。这样可以过滤掉95%的错误匹配，漏掉5%的正确匹配。

1.8 OPencv源码

#include "stdafx.h"
#include 
#include  
#include
#include"opencv2\core\core.hpp"
#include"opencv2\xfeatures2d.hpp"
#include "opencv2/highgui/highgui.hpp"
using namespace cv;
using namespace std;

int main()
{
    Mat src0 = imread("C:\\titleTemp.bmp",IMREAD_GRAYSCALE);
    Mat src1 = imread("C:\\test1.jpg",IMREAD_GRAYSCALE);

    if (src0.data == NULL || src1.data == NULL)
    {
        cout << "image no exist!" << endl;
        return -1;
    }

    Ptr sift = xfeatures2d::SIFT::create();
    vector keypoint0,keypoint1,keypointImg;

    Mat descriptor1, descriptor0;

    sift->detect(src0, keypoint0);
    sift->detect(src1, keypoint1);
    sift->compute(src0, keypoint0, descriptor0);
    sift->compute(src1, keypoint1, descriptor1);

    BFMatcher matcher;
    matcher.BRUTEFORCE_SL2;
    vector matches;

    matcher.match(descriptor0, descriptor1, matches);
    //排序
    sort(matches.begin(), matches.end());

    vector imgPt1, imgPt2;
    vector matchesVoted;

    for (int idx=0;idx <10;idx++)
    {
        DMatch dmatch;
        dmatch.queryIdx = idx;
        dmatch.trainIdx = idx;

        matchesVoted.push_back(dmatch);
        imgPt1.push_back(keypoint0[matches[idx].queryIdx]);
        imgPt2.push_back(keypoint1[matches[idx].trainIdx]);
    }

    Mat img_matches;
    std::vector< DMatch > emptyVec;
    drawMatches(src0, imgPt1, src1, imgPt2, matchesVoted, img_matches, DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS);
    imshow("SIFT_Match_Image", img_matches);
    waitKey();
    return 0;
}

2.0 Harris

原理参考：
[1]OpenCV Tutorials

代码出自OpenCV Tutorials：

    Mat src_gray = imread("C:\titleTemp.bmp", IMREAD_GRAYSCALE);

    Mat dst, dst_norm, dst_norm_scaled;
    dst = Mat::zeros(src_gray.size(), CV_32FC1);

    /// Detector parameters
    int blockSize = 2;
    int apertureSize = 3;
    double k = 0.04;

    /// Detecting corners
    cornerHarris(src_gray, dst, blockSize, apertureSize, k, BORDER_DEFAULT);

    /// Normalizing
    normalize(dst, dst_norm, 0, 255, NORM_MINMAX, CV_32FC1, Mat());
    convertScaleAbs(dst_norm, dst_norm_scaled);

    /// Drawing a circle around corners 
    for (int j = 0; j < dst_norm.rows; j++)
    {
        for (int i = 0; i < dst_norm.cols; i++)
        {
            if ((int)dst_norm.at<float>(j, i) > 128)
            {
                circle(dst_norm_scaled, Point(i, j), 5, Scalar(0), 2, 8, 0);
            }
        }
    }
    /// Showing the result
    namedWindow("Harris", CV_WINDOW_AUTOSIZE);
    imshow("Harris", dst_norm_scaled);
    waitKey();

    return 0;

3.0 Fast

3.1 原理：

Step1，如上图点p，点p对应的颜色值为I(p)，阈值t；在点p半径3内有16个像素点
Step2，如果16个点中有12连续点，其颜色值都I(p)-t，则为角点。
Step3，一种快速的尝试是通过排除一大部分非角点，这里只用到了1,9,5,13(如果1,和9的颜色值同时大于或小于Step2中的阈值，则检查3和5)，四个点中有三个满足条件(大于或小于)则为候选角点，对候选角点检测圆上所有的点做测试。上述算法效率较高，但有如下的缺点：
1，快速尝试角点容易跑丢
2，多特征情况下检测到的特征点离得近
3，当n<12不能拒绝过多候选点
4，检测出的角点不是最优的，这是因为它的效率取决于问题的排序与角点的分布

3.2 机器学习一个角点探测器Machine Learning a Corner Detector

Step1， 选取一系列图像，采用fast计算器特征点(feature points)
Step2， 对于每个特征点，保存16个点在一个vector中。获取所有图像的特征点vector P。
Step3， 对于点x，其包围的16个点包含如下三个状态：

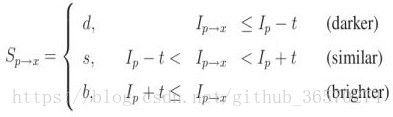
Step4， 则vector P包含三个子集(subsets)Pd,Ps,Pb，定义一个布尔变量(boolean variable)Kp,true为corner。
Step5， 采用决策树ID3，判断vector p

3.3 非极大值抑制Non-maximal Suppression

 从相邻多个角点选取最优角点是另一个问题，可以通过极大值抑制解决。
 1,定义一个相应函数(score function)V,V是点p同圆上像素点差的绝对值和。
 2,比较两个相邻特征点的V值，V值低的将被移除。

3.4 OPencv源码

Mat src0 = imread("C:\\Users\\Xue.Bicycle\\Desktop\\titleTemp.bmp", IMREAD_GRAYSCALE);
    Mat src1 = imread("C:\\Users\\Xue.Bicycle\\Desktop\\test1.jpg", IMREAD_GRAYSCALE);

    if (src0.data == NULL || src1.data == NULL)
    {
        cout << "image no exist!" << endl;
        return -1;
    }
    //fast
    Ptr fast = FastFeatureDetector::create(0);
    vector keypoint0, keypoint1;
    fast->detect(src0, keypoint0);
    fast->detect(src1, keypoint1);

    Ptr extractor = xfeatures2d::SiftDescriptorExtractor::create();
    Mat descriptor1, descriptor0;
    extractor->compute(src0, keypoint0, descriptor0);
    extractor->compute(src1, keypoint1, descriptor1);

    BFMatcher matcher;
    matcher.BRUTEFORCE_SL2;
    vector matches;

    matcher.match(descriptor0, descriptor1, matches);
    //排序
    sort(matches.begin(), matches.end());

    vector imgPt1, imgPt2;
    vector matchesVoted;

    if (0 == matches.size())
        return 0;

    for (int idx = 0; idx <10; idx++)
    {
        DMatch dmatch;
        dmatch.queryIdx = idx;
        dmatch.trainIdx = idx;

        matchesVoted.push_back(dmatch);
        imgPt1.push_back(keypoint0[matches[idx].queryIdx]);
        imgPt2.push_back(keypoint1[matches[idx].trainIdx]);
    }

    Mat img_matches;
    std::vector< DMatch > emptyVec;
    drawMatches(src0, imgPt1, src1, imgPt2, matchesVoted, img_matches, DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS);
    imshow("SIFT_Match_Image", img_matches);
    waitKey();
    return 0;

4.0 ORB(留坑待填)

5.0 SURF(留坑代填)

6.0 量化匹配度

量化背景：通过特征检测，匹配进行图像分类。保存一堆票据，保留其标题，根据标题的匹配度进行分类。如有不当之处，望指教！不胜感激

6.1 量化思路

 Step1:采用局部图像ImgTitle匹配整幅图像Img，匹配点的个数往往不能说明问题。通过观察我们知道，如果是匹配图像，则Img，ImgTitle的特征点之间在x,y方向的差值在等分辨率情况下具有一致性。即理想情况下差为0；
 Step2:将Img相邻特征点的差值Difx，Dify与ImgTitle相邻特征点归一化在同分辨率情况下。
 Step3:计算同分辨率差值Difx，Dify，Img与ImgTiltle的差值(相对分布的简单量化)。

6.2 代码：

    //keypointOri，keypoint分别为Img，ImgTitle的特征点。matches为暴力匹配法的结果。(接上述代码)
    vector<int> vScore, vScore1, vScoreOri, vScoreOri1;

    if (matches.size() <=1)
        return -1;

    int reNScore = 0;
    for (auto itr = matches.begin();itr != matches.end() - matches.size()/2;itr++)
    {
        Point2f p2f0 = keypointOri[itr->trainIdx].pt;
        Point2f p2f1 = keypointOri[(itr+1)->trainIdx].pt;

        vScoreOri.push_back(p2f0.x - p2f1.x);
        vScoreOri1.push_back(p2f0.y - p2f1.y);

        p2f0 = keypoint[itr->queryIdx].pt;
        p2f1 = keypoint[(itr + 1)->queryIdx].pt;

        vScore.push_back(p2f0.x - p2f1.x);
        vScore1.push_back(p2f0.y - p2f1.y);
    }
    float nScore = 0;
    float nScore_ = 0;

    for (int idx = 0; idx < std::min((int)10,(int)vScore.size()/10); idx++)
    {
        nScore += abs(vScore[idx]);
        nScore_ += abs(vScoreOri[idx]);
    }

    float fR;
    if (nScore == 0 || nScore_ == 0)
        return -1;
    else
    {
        fR = nScore / nScore_;
    }

    nScore = nScore_ = 0;
    for (int idx = 0; idx < vScore.size()/2; idx++)
    {           
        nScore += abs(vScoreOri[idx]*fR - vScore[idx]);
        nScore_ += abs(vScoreOri1[idx]*fR - vScore1[idx]);

    }
    return (nScore*0.8 + nScore_*0.2)/matches.size();