深度强化学习系列之(7): (重磅)强化学习《奖励函数》的设计和设置（reward shaping）

概述

前面已经讲了好几篇关于强化学习的概述、算法(DPG->DDPG),也包括对环境OpenAI gym的安装，baseline算法的运行和填坑，虽然讲了这么多，算法也能够正常运行还取得不错的效果，但是一直以来忽略了一个非常重要的话题，那就是强化学习的**《奖励函数》**的设置。

1、 Gym-Pendulum-v0例子分析奖励函数

为什么要讲强化学习的概述呢？也许在我们以前运行的算法中我们并没有直接接触到奖励函数的设置，而是直接调用了接口函数，下面以ddpg算法（点击查看DDPG算法）运行’Pendulum-v0’环境(下图，让摆杆立起来)为例子:

for j in range(MAX_EP_STEPS):
        if RENDER:
            env.render()
        # Add exploration noise
        a = ddpg.choose_action(s)
        # add randomness to action selection for exploration
        a = np.clip(np.random.normal(a, var), -2, 2)    
        s_, r, done, info = env.step(a)
        ddpg.store_transition(s, a, r / 10, s_)

这是episode运行过程，其中根据环境观察值得到action（ddpg.choose_action(s)）后, 直接将动作传给了env.step()函数了，于是我们就非常直接的得到了对应的奖励(Reward)、下一个状态($S^{‘}$)，随后直接开始考虑改善核心算法。

但是，我们忽略去研究强化学习中非常重要的奖励函数的设置，因为它会决定强化学习算法的收敛速度和程度。
那么到底env.step()背后是怎样的呢？

 def step(self, action, **kwargs):
        self._observation, reward, done, info = self.env.step(action)
        self._observation = np.clip(self._observation, self.env.observation_space.low, self.env.observation_space.high)
        return self.observation, reward, done, info

其中第三行np.clip()函数就是，大于max取max,小于min取min(查看clip()函数 )，然后继续追踪第二行self.env.step(action)，得到下面代码

 def step(self,u):
        th, thdot = self.state # th := theta
        g = 10.
        m = 1.
        l = 1.
        dt = self.dt
        u = np.clip(u, -self.max_torque, self.max_torque)[0]
        self.last_u = u # for rendering
        costs = angle_normalize(th)**2 + .1*thdot**2 + .001*(u**2)

        newthdot = thdot + (-3*g/(2*l) * np.sin(th + np.pi) + 3./(m*l**2)*u) * dt
        newth = th + newthdot*dt
        newthdot = np.clip(newthdot, -self.max_speed, self.max_speed) #pylint: disable=E1111

        self.state = np.array([newth, newthdot])
        return self._get_obs(), -costs, False, {}

这其实就是Pendulum-v0的奖励函数的设置本质，但是全是代码，并且是$\cos (\cdots ),\sin (\cdots )$,等函数，完全不知到从哪里来，当然还是能想到角度的，但是具体还要从其原理来讲：
Pendulum的角度和角速度，记为th和thdot，至于具体哪个角度我们将在后面进行分析。 此外，同样可以看出observation包括了cos(th)、sin(th)、thdot三个量。而在上文中我们知道action的定义，对于Pendulum问题来说，action space只有一个维度，就是电机的控制力矩，且有最大值和最小值的限制。其中cost是代价，且最终返回的奖励是-cost()

return self._get_obs(), -costs, False, {}

那么我们既可以对cost进行分析了：

costs = angle_normalize(th)**2 + .1*thdot**2 + .001*(u**2)

costs包含三项，
1、angle_normalize(th)2
2、1*thdot2，
3、001*(u**2)

第一项 这是对于当前倒立摆与目标位置的角度差的惩罚，那到底th表示哪个角度呢？对于angle_normalize()函数分析如下：

def angle_normalize(x):
    return (((x+np.pi) % (2*np.pi)) - np.pi)

我们先对$(x+\pi )$进行分析，带入几个角度，
比如$x=\pi /4，return=\pi /4$；$x=3\ast \pi /4，return=3\ast \pi /4$；$x=5*\pi/4，return=-3*\pi/4 $。这样我们就可以绘图如下

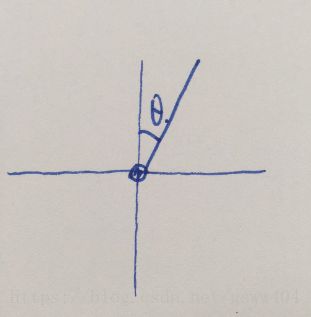
这就是我们的th， cos和sin都是大于-1小于1，thdot大于-8小于8，torque大于-2小于2，至于单位我们就不用考虑咯。
第二项表示对于角速度的惩罚，毕竟如果我们在到达目标位置（竖直）之后，如果还有较大的速度的话，就越过去了；至此，我们的分析就告一段落啦，
第三项是对于输入力矩的惩罚，我们所使用的力矩越大，惩罚越大，毕竟力矩×角速度=功率，还是小点的好。过程代码如图：

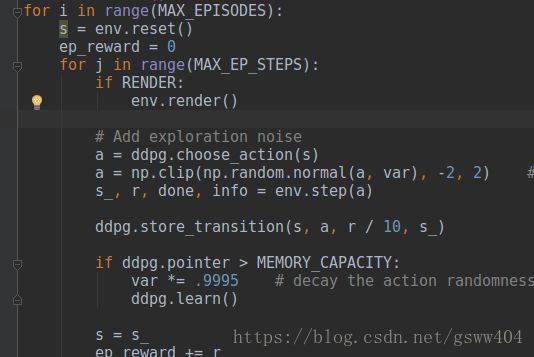
到这里，终于把一个例子的奖励函数分析了，也知道它的奖励和角度，力矩等有关。然而学习过程中我们却很少去关注，比如gym各种环境、Atari环境以及Deepmind的dm_control空间，所有的就是已经封装好的，但是我们自己怎样去设置一个奖励函数呢？reward很重要，因为强化学习就是基于 Reward Hypothesis(关于这个假设详见老爷子sutton【唠叨一句，老爷子可是强化学习的大师级人物，著有强化学习圣经《reinforcement learning: an introduction》，现在在Google工作】的页面：RewardHypothesis.)。这是假设所有的目标都可以被描述成最大化预期的累计的reward信号。

可能平时我们感觉不到奖励的区别，引用一故事：

---

举个我比较熟悉的例子吧，比如想让一个虚拟的人在虚拟环境下往前走。一种做法就是像openai或者deepmind那样，reward就是向前的速度，然后得到的结果就是一个很逗的行走姿态：https://deepmind.com/blog/producing-flexible-behaviours-simulated-environments/。 具体看链接里面那个小人手在疯狂摆动的往前行走。

进阶版是加上一个对于能量的penalty。也就是reward会扣除你所消耗的能量。如果运气好的话，那些多余的手部动作应该就不存在了，但是直接加这个penalty似乎效果不大。另一种就是，既然觉得那种动作太逗比了，我们就给他一个我们想让他做的动作。于是reward变成了和人行走姿态比有多大不同，于是得到了比较正常的结果：https://xbpeng.github.io/projects/DeepLoco/index.html结论：reward的影响很大。

---

2、 奖励函数设置

目前强化学习的奖励设置系统性介绍的文章特别少，查了很多资料，没有很多实质内容

Daniel Dewey在他的文章《Reinforcement Learning and the Reward Engineering Principle》提到了奖励函数（工程）的原则，原话是：
The Reward Engineering Principle: As reinforcement-learningbased AI systems become more general and autonomous, the design of reward mechanisms that elicit desired behaviours becomes both more important and more difficult.
翻译过来就是强化学习系统变得越来越普通的时候，引发期望行为的奖励机制的设计变得更加重要和困难！另外在奖励shaping中我们发现，奖励形成对强化学习速度的影响分析。 我们得出结论：奖励范围是一个重要的参数，它涉及整形的有效性，并证明它对于一个简单的强化学习算法在运行时间上具有最强的影响力。 此外，当学习利用奖励视界时，可以在不依赖于状态空间大小的情况下及时学习近似最优策略，而是根据视野内的状态数量。

（1）稀疏奖励（sparse reward）

稀疏奖励是最常见的一种奖励，在游戏中有很多的应用，即**“完成比赛得分，输掉比赛不得分”**这种形式。这个问题已经一直困扰了 RL 很多年了. 打个比方, 下围棋, 下的过程中是没有任何 reward 的, 只有下到最后才会出现一个 reward 信号说谁赢了. 这是很不好学的. 这一个 reward 信号很容易就消失在了茫茫的数据中(没有 reward 的数据). 而如果时时刻刻都有一个 reward 信号, 而且这个 reward 信号有小有大, sparse 的问题就很容易解决了. 所以做出一个好的 reward function 在现阶段很重要.
但是这种一般比较少，大多数在游戏中，至少我想到的周围的应用比较少，另外一个问题就是比较难，所以连续性的奖励就比较好，比如Atari游戏中的打砖块，打一个得一分，一个回合就是一次游戏得多少分，这样对于系统的学习也就响度简单点，后期遇到合适资料再进行补充。

（2）形式化奖励

在HalfCheetah环境中，我们有一个受限于一个垂直平面的双足机器人，这意味着它只能向前或向后运动。
机器人的目标是学会跑步步态，奖励是速度。这是一种形式化的奖励，机器人越接近奖励目标，系统给予的奖励就越多。这和稀疏奖励形成鲜明对比，因为这种奖励只在目标状态下给予奖励，在其他任何地方则没有奖励。这种形式化的奖励通常更容易促进学习，因为即使策略没有找到解决问题的完整解决方案，它们也能提供积极的反馈。具体的关于halfcheeath的原理如图:它是一个多自由度的控制,具体的是每个自由度上的速度,而计算奖励则是按照前后位置的位置进行计算.


它的奖励函数的源代码如下:

    def step(self, action):
        xposbefore = self.sim.data.qpos[0]
        self.do_simulation(action, self.frame_skip)
        xposafter = self.sim.data.qpos[0]
        ob = self._get_obs()
        reward_ctrl = - 0.1 * np.square(action).sum()
        reward_run = (xposafter - xposbefore)/self.dt
        reward = reward_ctrl + reward_run
        done = False
        return ob, reward, done, dict(reward_run=reward_run, reward_ctrl=reward_ctrl)

不幸的是，形式化的奖励也可能会影响学习效果。如前所述，它可能会导致机器人动作与预期不符。一个典型的例子是OpenAI的博文Faulty Reward Functions in the Wild，

（3）分布奖励

分布奖励思想来源于概率论中的分布,通常的做法是将奖励根据高斯分布等做,也有在rnn算法中通过记忆等做的,由于资料不多,故不详述.

（4）奖励系数变化奖励

这部分说起来比较简单，就是奖励是随其他变量而变化的，并不像前面的．比如：打保龄球，距离线的距离就可以算作每次发力的奖励。
　KaTeX parse error: No such environment: equation at position 17: …　R_{t} = \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \left\{ …

（5）中间难度起点奖励(SoID)

强化学习过程中经常会出现一个问题，刚开始学习全部是负面奖励，则学习起来很慢，但要是全部是积极奖励，系统又学不到不好的一面，于是科学家就提出了一种中间难度起点奖励，就是从中间开始的意思．
于是过程变成了记录目前实验对象的性能，为ＲＬ提供信号，特别关注策略梯度，通过采取预期总奖励的预计梯度来改变策略．数学描述为：
$${\nabla }_{\theta }J=\frac{1}{N}\sum _{i=1}{\nabla }_{\theta }\log {\pi }_{\theta }({\tau }^i)[R({\tau }^i,s_0^i)-R({\pi }_i,s_0^i)]$$
即目标在导向任务中，$R({\tau }^i,s_0^i)$ 是二元的，表示对象是否达到目标，所以常规的$R({\pi }_i,s_0^i)$ 用于计算从KaTeX parse error: Expected '}', got 'EOF' at end of input: s_{0]^{i}　开始的当前策略${\pi }_0$ 能否到达目标，为了避免开始训练从未达到或者已经掌握，英语了SoID概念，中间难度起点状态需要满足方程：
$$S_0:R_{min}<R({\pi }_i,s_0^i)<R_{max}$$
其中，$R_{min},R_{max}$　的值可以直接解释为从起点处开始自训练的最小／大概率．
后面继续补充…

---

设计须谨慎（例子）：

这里是一个例子，是设置负面奖励的，但是设置了之后不收敛了。。。。。
在探究多智能体通信合作时我们设计了这样一个实验，若干个小球通过碰撞将质量为自身200倍的大球推到target位置。

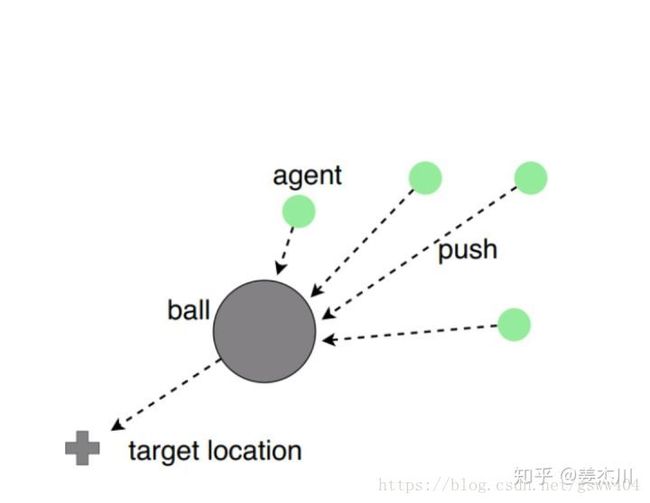
我们尝试过将reward设定为如果从大球背离target的一侧发生碰撞，则获得正的reward（符合人类的策略）。在这种设定下，我们发现小球们会很快学会从一侧撞击来推动大球的策略。这时我们稍微修改了reward函数，在原reward基础上，添加当小球在大球靠近target的一侧发生撞击时，获得一个极小的负reward（不能从另一侧阻碍推动）结果是：完全不收敛猜想的原因可能是这个reward的function局部最优的底可能特别宽吧，陷进去就出不来

---

持续更新，部分还没有写完…敬请期待！

参考文献：
[1].https://blog.csdn.net/u013745804/article/details/78397106
[2].https://www.zhihu.com/question/277172900
[3].https://mp.weixin.qq.com/s?__biz=MzI3ODkxODU3Mg==&mid=2247485609&idx=1&sn=6b71f5f8ebd4e920384f07b97ce92a9c&chksm=eb4eec6adc39657c81169f1ae9ce477e4da692941238c35deb26a11ed7ec70073784cfd935a8#rd
[4].https://medium.com/@BonsaiAI/deep-reinforcement-learning-models-tips-tricks-for-writing-reward-functions-a84fe525e8e0
[5].http://bair.berkeley.edu/blog/2017/12/20/reverse-curriculum/
[6].https://www.jqr.com/news/009376