【Python】【matplotlib】绘图函数

对数坐标图

根据x, y 轴分别是否为对数，总共4种：

plot()
semilogx()
semilogy()
loglog()

示例

import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(1,10,1000)
y=np.sin(x)

plt.subplot(221)
plt.plot(x,y)
plt.subplot(222)
plt.semilogx(x,y)
plt.subplot(223)
plt.semilogy(x,y)
plt.subplot(224)
plt.loglog(x,y)

plt.show()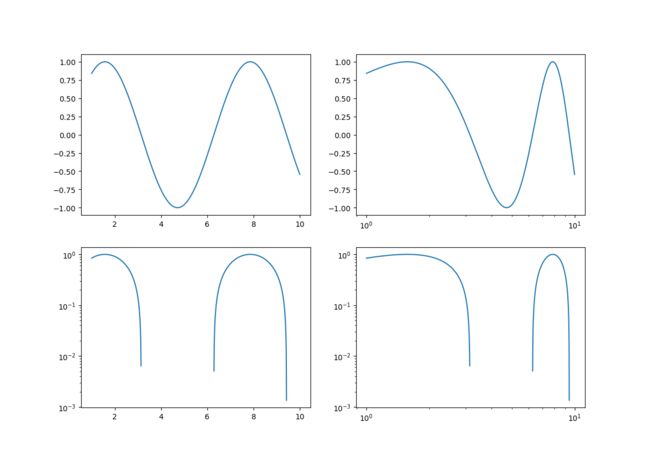

http://www.guofei.site/public/postimg2/matplotlib3_1.png‘>

极坐标绘图

仅需要这样：

plt.subplot(111,polar=True)

示例

import numpy as np
import matplotlib.pyplot as plt
theta=np.linspace(0,2*np.pi,100)
rho=1-np.sin(theta)
plt.subplot(111,polar=True)
plt.plot(theta,rho)
plt.show()

http://www.guofei.site/public/postimg2/matplotlib3_2.png‘>

bar

就是bar啦！

import numpy as np
import matplotlib.pyplot as plt

x = np.array([1, 2, 3, 4, 5])
y1 = x
y2 = x ** 1.5

width = 0.2
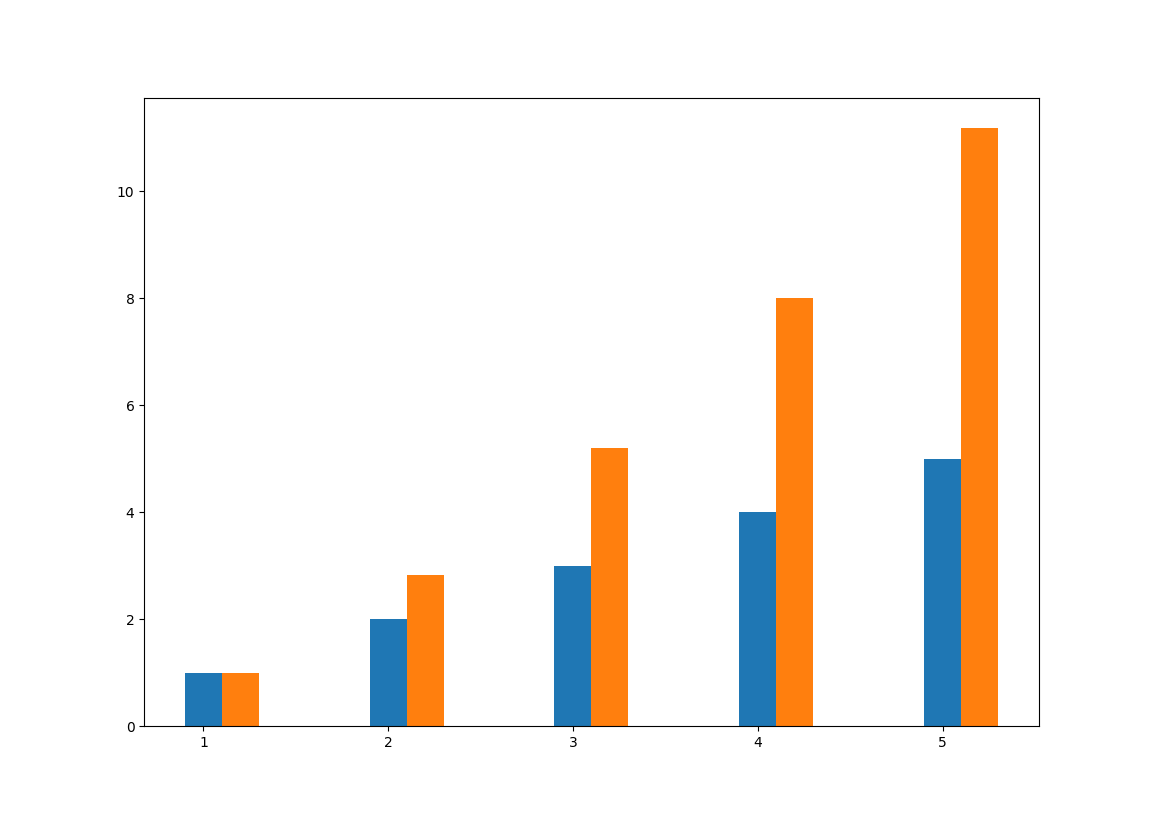
plt.bar(x, y1, width)
plt.bar(x + width, y2, width)
plt.show()

这里做了个小技巧，用width作为偏移，画出多个bar

http://www.guofei.site/public/postimg2/matplotlib3_3.png‘>

scatter

scatter与plot的不同是，scatter可以分别指定每个点的大小和颜色

import matplotlib.pyplot as plt
from scipy.stats import uniform

rv=uniform(loc=0,scale=1)

x=rv.rvs(size=100)
y=rv.rvs(size=100)

plt.scatter(x,y,s=x*1000,c=y,marker=(5,1))
plt.show()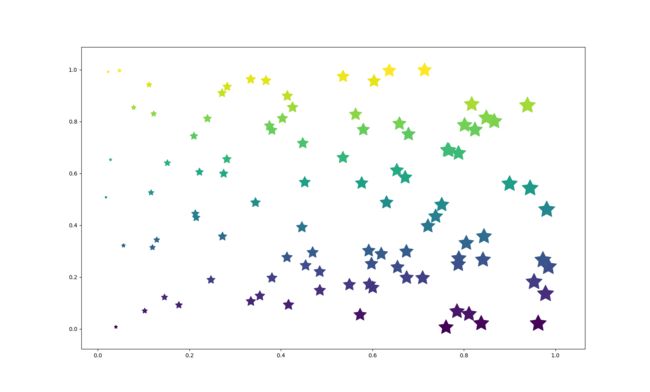

http://www.guofei.site/public/postimg2/matplotlib3_4.png‘>

按照输入顺序，scatter的输入值分别代表：
1. 每个点的X坐标
2. 每个点的Y坐标
3. s参数指定点的大小（值和点的面积成正比）
4. c参数指定点的颜色，可以是数值或数据。
- 如果是数值则自动调用颜色映射表
- 如果是(N,3)或(N,4)数组，则代表RGB颜色
5. marker指定形状
- 第一个元素代表顶点数量
- 第二个元素代表样式
- 0多边形
- 1星形
- 2放射形
- 3圆形（忽略边数）

image

imread()：读入图像
imshow()：输出图像

img=plt.imread('unicorn.png')

对于彩色图像，返回的img是一个array，大小是(M,N,C)，其中，
- M是图像的高度
- N是图像的宽度
- C=3&4是颜色通道
对于灰度图像，返回的array，大小是(M,N)
img取值范围是0~1

等高图

contour()#等高线
contourf()#带填充效果的等高线

示例1

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm

x = np.linspace(-3.0, 3.0, 100)
y = np.linspace(-2.0, 2.0, 80)
X, Y = np.meshgrid(x, y)
Z = X * np.exp(-X ** 2 - Y ** 2)

fig = plt.figure(1)
ax1 = plt.subplot(121)
ax2 = plt.subplot(122)
cs1 = ax1.contour(X, Y, Z, 10)
cs2 = ax2.contourf(X, Y, Z, 10, cmap=cm.PuBu_r)

cbar = fig.colorbar(cs2)  # 在figure上添加cs2对应的颜色条
plt.clabel(cs1)  # 在cs1的等高线上添加数字
plt.show()

http://www.guofei.site/public/postimg2/matplotlib3_5.png‘>

示例2：隐函数的解

加入levels这个参数，可以画出对应的等高图，依次来画出隐函数的解，
下面的代码是画出 f=(X2+Y2)∗∗4−(X2−Y2)2 , 在 f=0,f=0.5 处的解。

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-1.5, 1.5, 100)
y = np.linspace(-1.5, 1.5, 80)
X, Y = np.meshgrid(x, y)
Z = (X ** 2 + Y ** 2) ** 4 - (X ** 2 - Y ** 2) ** 2

ax = plt.subplot(111)
cs = ax.contour(X, Y, Z, 10, levels=[0, 1], colors=['b', 'r'], linestyles=['-', ':'], linewidths=[2, 2])

plt.clabel(cs)
plt.show()

<

需要注意的是，由于源数据是离散值，所以等高图在某些区域是离散的片段，但实际上应当是连续值。

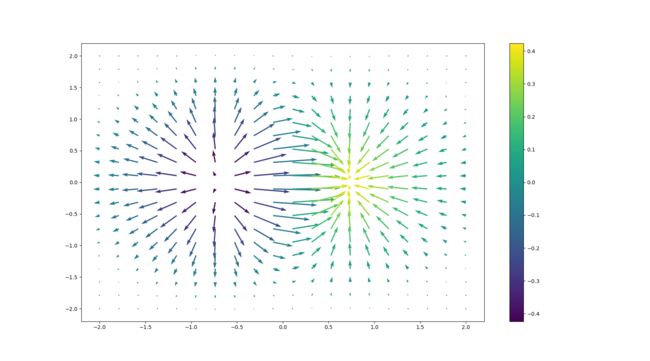
箭头图

quiver(X,Y,U,V,C)

• X, Y代表箭头起点的坐标
• U, V代表箭头对应的向量
• C代表颜色

示例

import numpy as np
import matplotlib.pyplot as plt


def f(x, y):
    return x * np.exp(-x ** 2 - y ** 2)


def dev_f(f, x, y, dx=1e-6, dy=1e-6):
    v = f(x, y)
    vx = (f(x + dx, y) - v) / dx
    vy = (f(x, y + dy) - v) / dy
    return vx, vy


X, Y = np.meshgrid(np.linspace(-2, 2, 20), np.linspace(-2, 2, 20))
U, V = dev_f(f, X, Y)
C = f(X, Y)

plt.quiver(X, Y, U, V, C)
plt.colorbar()
plt.show()