聚类分析：基于密度聚类的DBSCAN算法

对于簇形状不规则的数据，像k-means（聚类分析: k-means算法）这种基于划分的方法就不再适用了，因为划分方法（包括层次聚类算法）都是用于发现“球状簇”的。比如下面两个图中，Fig.1所示的数据分布用k-means作聚类是没有问题的，但是对于Fig.2就不行了，会把大量的噪声或者离群点也包含在簇中。

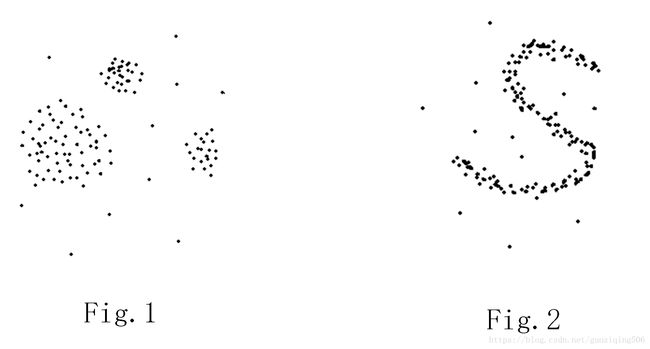
解决这种任意簇形状的聚类问题，就要采用一种与划分聚类或者层次聚类不同的聚类方法——基于密度聚类。对于基于密度的聚类，最常用的算法就是本文要说的DBSCAN（Density-Based Spatial Clustering of Application with Noise），简单直译过来就是“具有噪声应用的基于密度的空间聚类”。

概念介绍

在讲解DBSCAN具体的工作原理之前，先介绍关于这个算法的一些专门定义的概念。

• 核心对象：一个数据点可被称为核心对象，如果以这个数据点为球心，以长度 ϵ ϵ 为半径的超球面区域内，至少有 MinPts M i n P t s 个数据点。为了后面叙述简单，我将这个核心对象称为 (ϵ,MinPts) ( ϵ , M i n P t s ) -核心对象，将它的这个球面区域称为核心对象的 ϵ ϵ -邻域。

• 直接密度可达：对于 (ϵ,MinPts) ( ϵ , M i n P t s ) -核心对象 O1 O 1 和对象 O2 O 2 ，我们说 O2 O 2 是从 O1 O 1 直接密度可达的，如果 O2 O 2 在 O1 O 1 的 ϵ ϵ -邻域内。注意，这里只要求 O1 O 1 是核心对象，而 O2 O 2 可以是任意对象（数据点）。也就是说，定义“A从B（或从B到A）直接密度可达”中，作为出发点的 B B 一定得是核心对象。

• 密度可达：从核心对象 O1 O 1 到对象 On O n （这里同样不要求 On O n 是核心对象）是密度可达的，如果存在一组对象链 {O1,O2,…,On} { O 1 , O 2 , … , O n } ，其中 Oi O i 到 Oi+1 O i + 1 都是关于 (ϵ,MinPts) ( ϵ , M i n P t s ) 直接密度可达的。实际上，从这个定义我们不难看出， {O1,O2,…,On−1} { O 1 , O 2 , … , O n − 1 } 都必须是核心对象。

• 密度相连：两个对象 O1,O2 O 1 , O 2 （注意，这里不要求是核心对象）是密度相连的，如果存在一个对象 p p ，使得 p p 到 O1 O 1 ， p p 到 O2 O 2 都是密度可达的。这个定义是对称的，即 O1 O 1 与 O2 O 2 是密度相连的，则 O2 O 2 与 O1 O 1 也是密度相连的。

上面4个定义中，后两个容易混淆。其实可以这样想，所谓密度可达，是说可以“一条道”走过去；而所谓密度相连，是说可以找到一个中间点，从这个中间点出发，可以分别“一条道”走到两边。

关于密度相连的理解是整个DBSCAN算法的核心，他实际代表的意义可以这样理解：对于任意形状的簇来说，一定存在这样一个点，使得组成这个簇的点都能从这个点出发，通过一条“稠密”的路径到达。换句话说，簇中的点一定是相互密度相连的。

还有两个区别于“核心对象”的概念，那就是“噪声对象”和“边缘对象”。在用DBSCAN对数据做聚类分析时，“噪声对象”也是一个非常重要的结果。所以，最好的算法是在给出聚好的类之外，也给出噪声点。为了让整个算法看起来清晰，我在讲解算法步骤之前，先给出“噪声对象”和“边缘对象”的定义。

• 噪声对象：不是核心对象，且也不在任何一个核心对象的 ϵ ϵ -邻域内；
• 边缘对象：顾名思义是类的边缘点，它不是核心对象，但在某一个核心对象的 ϵ ϵ -邻域内；

总之，对于数据集中的任意一个点，它要么是核心对象，要么是噪声对象，要么是边缘对象。

算法思路

现在我们来思考怎样解决非球状簇的聚类问题。直观上来想象，既然是要找任意形状的簇，那么最直接的办法是先找到一个核心对象，再找到与这个核心对象密度相连的所有点，这些点将构成这个簇。比如下图中，假设当前我们要找的簇是外层的圆圈，很显然，内层圆上的点与外层圆圈上的点肯定不是密度相连的，而且其他的离群点与外层这个圆圈的点也不是密度相连的。所以，只要我们选择合适的参数，就一定可以通过簇中的任意一个核心对象，拓展找到所有的簇中所有的点（当然，这些点都是密度相连的）。

具体算法的工作原理可以这样来设计：

初始化阶段，给所有数据点赋一个unvisited的属性，表示这个数据点未被访问；

1.在所有属性为unvisited的点集中，随机找一个点 p p ，标记为visited；

2.检查它是否为核心对象，若不是，标记 p p 为噪声点，再重新开始寻找（像第1步中那样）；若是，则执行后面的步骤；

注1：前两部的目的在于找到一个核心对象，作为一个新簇的初始（第一个）对象。
注2：2步中标记为噪声的点不一定真的是噪声点，它也有可能是边缘点，所以如果要得到准确的噪声集合，需要在后面做进一步筛选。

既然找到了第一个核心对象，接下来的步骤就是创建第一个类了（记为 C C ）：

3.建立一个候选集 Candidates C a n d i d a t e s ，初始时， Candidates C a n d i d a t e s 中只有一个元素，那就是上一步找到的核心对象；

4.对于 Candidates C a n d i d a t e s 中的每一个对象（记为 p p ），做以下操作：
(1) 若 p p 还未被聚到任意一个类，则加入类 C C ；
(2) 若 p p 是核心对象，则将它的 ϵ ϵ -邻域内的，除了当前类 C C 的点之外的点（也就是 Candidates−C C a n d i d a t e s − C ）加入 Candidates C a n d i d a t e s ；
(3) 若 p p 在噪声集合内，将它从噪声集合移除（因为肯定不是噪声）；
(4) 若 p p 的属性是unvisited，则标记为visited；

注：（3）（4）两步属于常规操作，无需多想，重点在于（1）（2）步。因为 Candidates C a n d i d a t e s 中的每一个对象要么是核心对象，要么是核心对象的 ϵ ϵ -邻域内的点，所以肯定和其核心对象是直接密度可达的，进而可以知道 Candidates C a n d i d a t e s 中的这些点都是密度相连的。所以当 p p 还不属于任何类时，我们可以毫不犹豫地将 p p 加入类 C C ；（2）步中需要注意的是，因为当前类 C C 的点已经分析过了，所以不用再次加入 Candidates C a n d i d a t e s 了，否则会导致一个死循环。

5.循环执行第4步，直到 Candidates C a n d i d a t e s 中找不到核心对象为止，这说明当前这个类已经被找完全了。

6.返回第1步，开始找下一个簇。直到所有的点都变成visited.

代码实现

下面，我将给出实现代码。首先，为了验证代码的正确性，我造了一个数据集（没办法，找资料的能力差，实在在网上找不到特别合适的），这个数据集的图像画出来如下图所示：

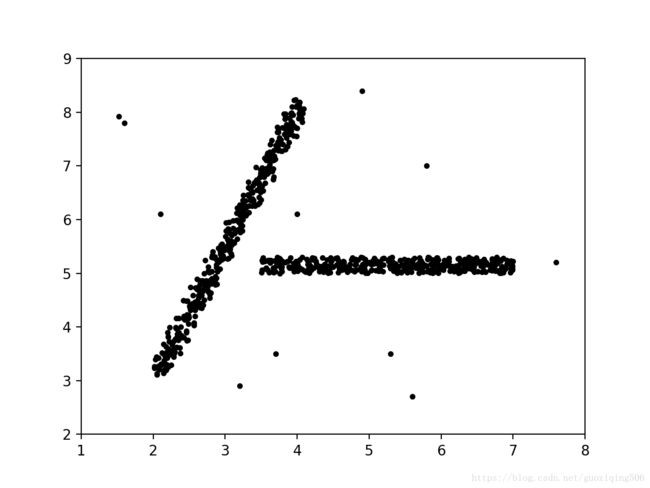
具体的数据集我保存了一个csv文件，在文章最后给出的我的github主页里，名字叫”data.csv”。然后根据上面算法的工作原理，给出实现代码。

首先是建一个数据对象的类，方便写后面的算法：

import numpy as np


class DataPoint(object):
    def __init__(self, coordinates):
        """
        :param coordinates: the ndarray object
        """
        self.coordinates = coordinates
        self.neighborhood = set()

    def isCore(self, db, radius, minPts):
        """

        :param db: the database whose elements are DataPoint objects.
        :param radius: the radius of a point's neighborhood
        :param minPts:
        :return:
        """
        for i in db:
            if np.linalg.norm(self.coordinates - i.coordinates) <= radius:
                self.neighborhood.add(i)

        if len(self.neighborhood) >= minPts:
            return True
        return False

然后给出聚类算法：

def dbscan(db, radius, minPts):
    """

    :param db:
    :param radius:
    :param minPts:
    :return:
    """
    visited = set()
    noise = set()
    results = []

    while len(visited) < len(db):

        core = None
        C = set()

        # find the core point
        temp = set()
        for point in db - visited:
            temp.add(point)
            if point.isCore(db - {point}, radius, minPts):
                core = point
                break
            else:
                noise.add(point)
        visited.update(temp)

        # can't find any core point, i.e., the cluster process should be terminated
        if not core:
            break

        # construct the new cluster C
        flag = True
        candidates = {core}

        # flag denotes whether there is at least one core point in candidates
        while flag:

            flag = False
            tempCandidates = set()
            for member in candidates:

                # remove the boundary points in noise
                if member in noise:
                    noise.remove(member)

                # label the cur as visited
                if member not in visited:
                    visited.add(member)

                # if cur not belongs to other clusters, add it in the cluster C
                belongToOtherCluster = False
                for cluster in results:
                    if member in cluster:
                        belongToOtherCluster = True
                        break
                if not belongToOtherCluster:
                    C.add(member)

                # if cur is core, add its neighborhood in tempCandidates
                if member.isCore(db - {member}, radius, minPts):
                    tempCandidates.update(member.neighborhood - C)
                    flag = True
            candidates = set() | tempCandidates
        results.append(C)
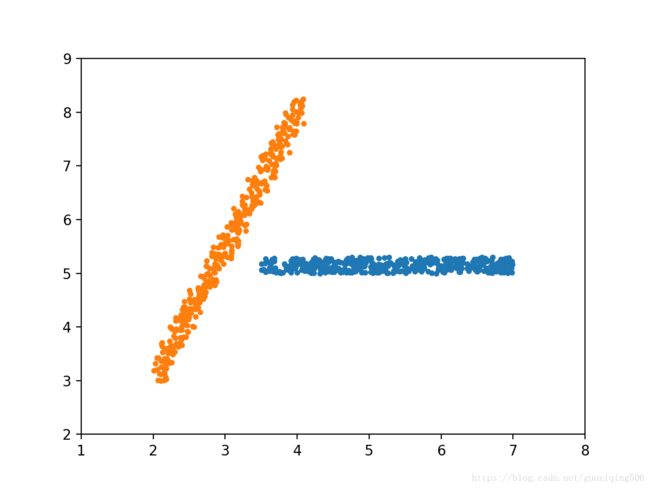
    return results

根据我的数据点，我调整参数 (ϵ,MinPts) ( ϵ , M i n P t s ) 为 (0.2,3) ( 0.2 , 3 ) ，最后清晰地得到两个类，作图如下：

完整的实现代码，包括如何生成数据集，DBSCAN算法，还有作图的函数都在我的github主页里：DBSCAN，欢迎大家参考挑错。