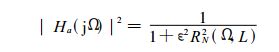椭圆滤波器与巴特沃斯、切比雪夫的比较和实现
椭圆滤波器(Elliptic filter)又称考尔滤波器(Cauer filter):这是在通带和阻带等波纹的一种滤波器。椭圆滤波器相比其他类型的滤波器,在阶数相同的条件下有着最小的通带和阻带波动。它在通带和阻带的波动相同,这一点区别于在通带和阻带都平坦的巴特沃斯滤波器,以及通带平坦、阻带等波纹或是阻带平坦、通带等波纹的切比雪夫滤波器。
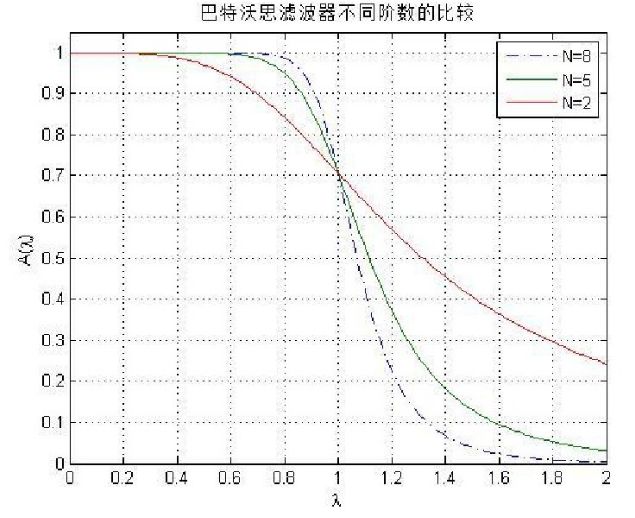
首先看看巴特沃斯滤波器的频响特性:
可以看出巴特沃斯的通带和阻带都十分平缓
接下来是切比雪夫滤波器频响曲线:
看得出来,切比雪夫是阻带平稳,通带等波纹。
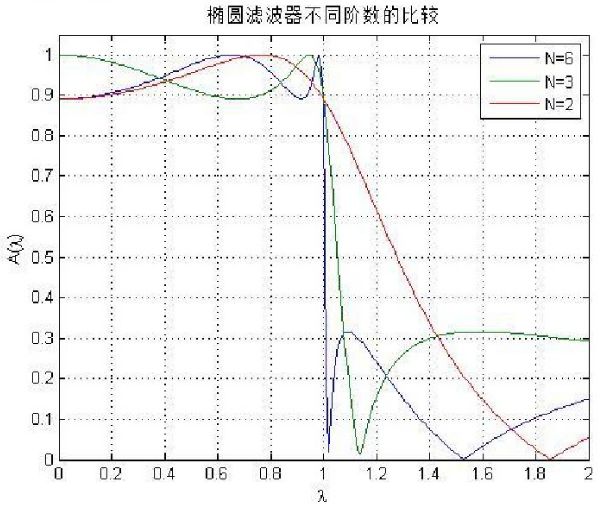
接下来是椭圆滤波器:
可以看出,三种滤波器中,椭圆滤波器的过渡带最窄,但通带和阻带都是等波纹的,也就是说过渡带的特性是由牺牲阻带和通带的稳定性换来的。
而对于相同的性能要求,它所需要的阶数最低。
对于模拟椭圆滤波器,振幅平方函数为:
式中 R N(Ψ, L) 为雅可比椭圆函数 ; L 是一个表示波纹性质的参量 。其特性曲线如下图所示 。
可以看出,在归一化通带内,R()在(0,1)之间振荡,而超过Ω之后,R在(L^2,∞)之间振荡,这一特点使得滤波器同时 在通带和阻带具有任意衰减量。
下图是典型的N为奇数的椭圆滤波器的幅度特性:
由于模拟滤波器的设计方法非常成熟 ,许多典型系统有成熟的公式 、图表可以查阅 ,便于设计 ; 因此设计数字滤波器的主要方法是 : 首先设计一个合适的模拟滤波器 , 然后将他 “ 变换 ” 成满足给定指标的数字滤波器 。
设计椭圆滤波器的四个步骤:
1.确定数字滤波器性能指标:: ω p , ω s , Ap , A s
2.将数字滤波器性能指标转换成相应的模拟滤波器性能指标 ;
3.设计满足指标要求的模拟滤波器 H a(s)
4.通过变换将模拟滤波器转换成数字滤波器 。
椭圆滤波器的MATLAB实现:
库函数:: ellipord 函数和 ellip 函数
ellipord 函数的功能是求滤波器的阶数 。该函数可以得到数字椭圆型滤波器的最小阶数 n 和截止频率 Wn ,并使滤波器在通带内(0 , Wp)的波纹系数小于通带最大衰减 R p ,阻带内(W s , 1)的波纹系数大于阻带最小衰减 R s
ellip 函数的功能是设计滤波器 ,[ b, a] = ellip(n , R p , R s , Wn), 利用 ellipord 函数得到的最小阶数 n 和截止频率 Wn ,可以设计低通 、或带通滤波器(当 W n =[ W 1 , W 2] 时)。
例如 : 设计一个带通椭圆数字滤波器 , 通带为 100 ~250 H z,过渡带均为 50 H z,通带波纹小于 3 db ,阻带衰减为 30 db ,采样频率 f s =1 000 H z 。其程序为 :
fs = 1000 ;
Rp =3; Rs =30 ;
Wp =2 *[ 100 200] /fs;
W s = 2 *[ 50 250] /f s;
[ n , W n] = ellipo rd (Wp , W s , Rp , Rs);
[ b , a] = ellip(n , Rp, Rs Wn);
freqz (b, a, 512 , fs)
程序运行结果如下图所示 :