A*算法求解八数码--演示程序(MFC)
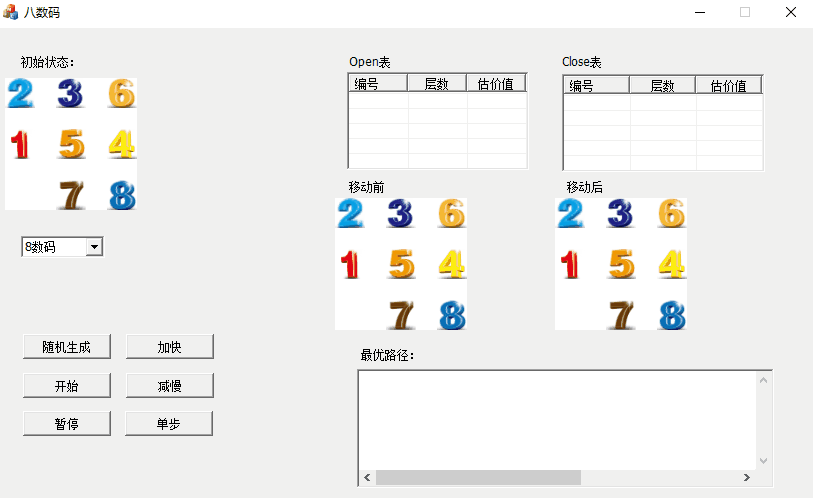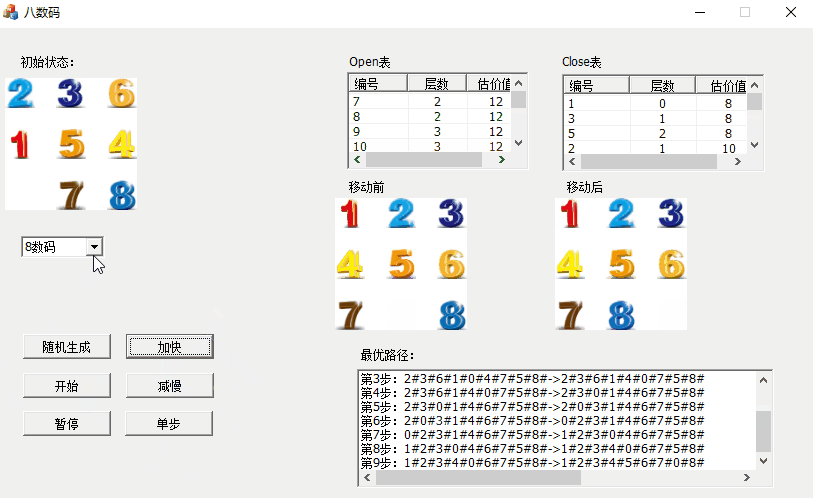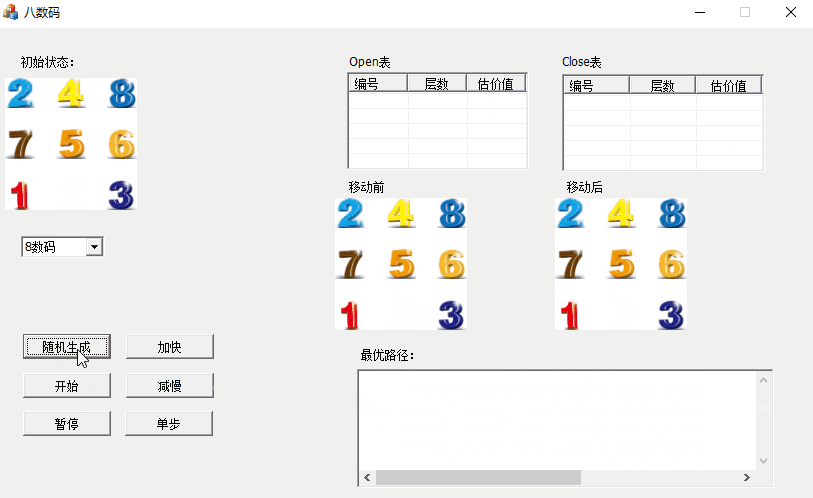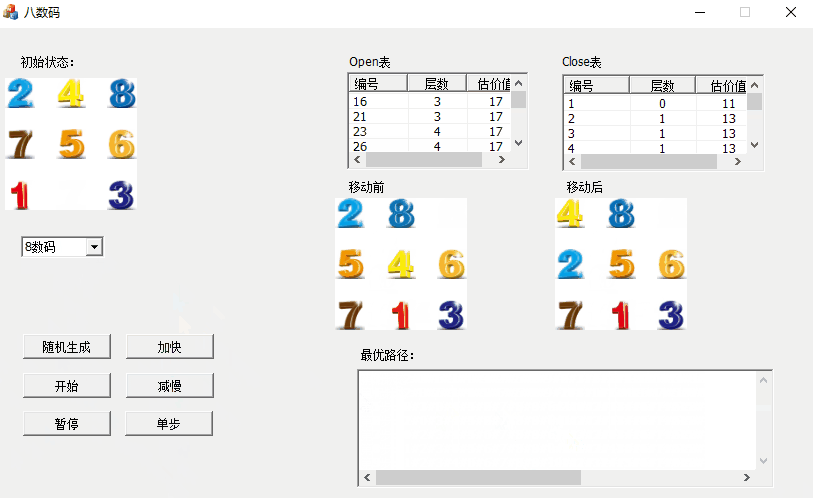
首先看看程序的运行效果
一、程序功能:
1、单步或者连续演示用A*解决八数码或者十五数码难题的步骤,可暂停。
2、随机生成初始状态。
3、调节演示速度(加快与减慢)
4、open表与close表对应存储的为未扩展结点和已扩展的结点。
5、演示完毕,显示最优路径。
二、预备知识
1、八数码与A*算法
A*算法:A*算法是一种有序搜索算法,其特点在于对估价函数的定义上。对于一般的有序搜索,总是选择f值最小的节点作为扩展节点。因此,f是根据需要找到一条最小代价路径的观点来估算节点的,所以,可考虑每个节点n的估价函数值为两个分量:从起始节点到节点n的代价以及从节点n到达目标节点的代价。
八数码中的代价函数为f(n)=g(n) + w(n)。其中w(n)为搜索深度,目标状态对应的深度为0,由目标状态扩展的节点的状态的深度为1,接着扩展的深度为2,3……等;g(n)为从当前状态到目标状态所需的最小步数。具体代码如下:
//求解从当前状态到目标状态最少需要多少步
int CalWeight(int * a, int n)
{
int res = 0, x, y, col = sqrt(n + 1);
for (int i = 0; i <= n; ++i)
{
if (a[i] == 0)
continue;
for (int j = 0; j <= n; ++j)
{
if (EndState[j] == a[i])
{
x = j / col;
y = j % col;
break;
}
}
res = res + abs(i / col - x) + abs(i % col - y);
}
return res;
}
八数码:在一个3*3的方棋盘上放置着1,2,3,4,5,6,7,8八个数码,每个数码占一格,且有一个空格。这些数码可以在棋盘上移动,其移动规则是:与空格相邻的数码方格可以移入空格。经有限步数或者不可能从起始状态到达目标状态。
2、八数码有解判断
逆序数:一个序列中,每个数字的前面比本数字大的数字的个数的总和。
代码如下:
//计算逆序数
int inver(int s[], int number)
{
int sum = 0;
for (int i = 0;i<= number;i++)
{
if (s[i] == 0) continue;
for (int j = i - 1;j >= 0;j--)
if (s[j]>s[i]) sum++;
}
return sum;
}
若起始状态与目标状态的逆序数的奇偶性一致,则认为两个状态可达,否则不可达。
证明见:八数码问题是否可解
3、标记八数码搜索过程中已访问的状态
常用的哈希函数,散列值是通过康托展开得到。但此方法仅限于数字序列小于10,不然映射数字过大。
康托展开与逆展开的代码如下:
//康托展开式及逆展开
static const int FAC[] = { 1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880 }; // 阶乘
int cantor(int *a, int n)
{
int x = 0;
for (int i = 0; i <= n; ++i) {
int smaller = 0; // 在当前位之后小于其的个数
for (int j = i + 1; j <= n; ++j) {
if (a[j] < a[i])
smaller++;
}
x += FAC[n - i] * smaller; // 康托展开累加
}
return x; // 康托展开值
}//康托展开逆运算
void decantor(int x, int * a, int n)
{
int idx = 0;
vector v; // 存放当前可选数
for (int i = 0;i <= n;i++)
v.push_back(i);
for (int i = n;i >= 0;i--)
{
int r = x % FAC[i];
int t = x / FAC[i];
x = r;
sort(v.begin(), v.end());// 从小到大排序
a[idx++] = v[t]; // 剩余数里第t+1个数为当前位
v.erase(v.begin() + t); // 移除选做当前位的数
}
} N数码的通用标记方法,我采用的是set去重,数字转成字符串('#'分隔)
//数字转字符串(用'#'分隔)
string NumToStr(int *a, int n)
{
string res("");
char ch[5];
for (int i = 0; i <= n; ++i)
{
sprintf(ch, "%d", a[i]);
res = res + ch;
res.push_back('#');
}
return res;
}
//字符串转数字
void StrToNum(string str, int *a, int n)
{
int idx = 0, i = 0, tmp = 0, num = 0;
while (str.find('#', idx) != -1)
{
tmp = idx;
idx = str.find('#', idx);
num = 0;
for (int j = tmp; j < idx; ++j)
{
num = num * 10 + (str[j] - '0');
}
a[i++] = num;
idx++;
}
}三、程序局部功能实现
1、绘制界面,分为三部分:起始状态,移动前状态,移动后状态。代码如下:
//显示三个状态(重绘界面)
//初始状态,移动前,移动后
//运行程序时,若界面显示异常,可尝试电脑的显示设置中"更改文本、应用等项目大小"是否为100%
void CEightFigureDlg::ShowFigure(CDC * dc)
{
//显示背景
CDC pdc, ddc;
pdc.CreateCompatibleDC(dc); // 创建一个临时显示设备
ddc.CreateCompatibleDC(dc); // 创建一个加载盘子的临时显示设备
CBitmap bmp, *obmp;
int step;
switch (number)
{
case 8:
step = 51;
break;
case 15:
step = 33;
break;
}
bmp.LoadBitmap(IDB_BG1); // 加载背景图片
obmp = pdc.SelectObject(&bmp); // 将图片显示在设备pdc上。
for (int i = 0, col = sqrt(number + 1); i <= number; i++)
{
CBitmap dbmp, *odbmp;
dbmp.LoadBitmap(IDB_Num0 + StartState[i]); // 加载数字图片
odbmp = ddc.SelectObject(&dbmp); // 将盘子显示在设备ddc上。
pdc.BitBlt(0 + (i % col)* step, 0 + (i / col) * step, 30, 30, &ddc, 0, 0, SRCCOPY); // 将ddc拷贝到临时显示设备pdc对应位置上
ddc.SelectObject(odbmp); // 显示完毕,还原设备
}
dc->BitBlt(10, 50, 132, 132, &pdc, 0, 0, SRCCOPY); // 将ddc拷贝到临时显示设备pdc对应位置上
pdc.SelectObject(obmp); // 显示完毕,还原设备
obmp = pdc.SelectObject(&bmp); // 将图片显示在设备pdc上。
for (int i = 0, col = sqrt(number + 1); i <= number; i++)
{
CBitmap dbmp, *odbmp;
dbmp.LoadBitmap(IDB_Num0 + NowState[i]); // 加载数字图片
odbmp = ddc.SelectObject(&dbmp); // 将盘子显示在设备ddc上。
pdc.BitBlt(0 + (i % col) * step, 0 + (i / col) * step, 30, 30, &ddc, 0, 0, SRCCOPY); // 将ddc拷贝到临时显示设备pdc对应位置上
ddc.SelectObject(odbmp); // 显示完毕,还原设备
}
dc->BitBlt(340, 170, 132, 132, &pdc, 0, 0, SRCCOPY); // 将ddc拷贝到临时显示设备pdc对应位置上
obmp = pdc.SelectObject(&bmp); // 将图片显示在设备pdc上。
for (int i = 0, col = sqrt(number + 1); i <= number; i++)
{
CBitmap dbmp, *odbmp;
dbmp.LoadBitmap(IDB_Num0 + NextState[i]); // 加载数字图片
odbmp = ddc.SelectObject(&dbmp); // 将盘子显示在设备ddc上。
pdc.BitBlt(0 + (i % col) * step, 0 + (i / col) * step, 30, 30, &ddc, 0, 0, SRCCOPY); // 将ddc拷贝到临时显示设备pdc对应位置上
ddc.SelectObject(odbmp); // 显示完毕,还原设备
}
dc->BitBlt(560, 170, 132, 132, &pdc, 0, 0, SRCCOPY); // 将ddc拷贝到临时显示设备pdc对应位置上
//dc->BitBlt(10, 10, 300, 300, &pdc, 0, 0, SRCCOPY); // 将pdc拷贝到程序显示设备dc上
//pdc.SelectObject(obmp); // 显示完毕,还原设备
}
2、程序中要实现连续,单步,速度可调,可暂停。使用定时器Timer,调节速度,可调整第二个参数的大小。
具体代码如下:
OnTimer(UINT nIDEvent)
//定时器执行函数
void CEightFigureDlg::OnTimer(UINT nIDEvent)
{
switch (nIDEvent)
{
case 602:
int col = sqrt(number + 1);
if(!que.empty())
{
Node now = que.top();
que.pop();
//decantor(now.cantorVal, NowState, number);
StrToNum(now.str, NowState, number);
if (CalWeight(NowState, number) == 0)
{
//MessageBox(_T("结束了"));
KillTimer(602);
}
v2.push_back(now);
//更新open表
CListCtrl *List = (CListCtrl *)GetDlgItem(IDC_LIST2);
int len = m_OpenListCtrl.GetItemCount();//取行数
CString itemText;
for (int row = 0;row < len; row++)
{
itemText = List->GetItemText(row, 0);
if (_ttoi(itemText) == now.rank)
{
List->DeleteItem(row);
break;
}
}
//m_OpenListCtrl.DeleteItem();
//MyDeal(now.rank);
//更新close表
CString str;
int rows = m_ClosedListCtrl.GetItemCount();
str.Format("%d", now.rank);
m_ClosedListCtrl.InsertItem(rows, str);
str.Format("%d", now.depth);
m_ClosedListCtrl.SetItemText(rows, 1, str);
str.Format("%d", now.val);
m_ClosedListCtrl.SetItemText(rows, 2, str);
int idx, depth, val;
for (idx = 0; idx <= number; ++idx)
{
if (NowState[idx] == 0)
break;
}
int a = idx / col, b = idx % col;
string oldStr = NumToStr(NowState, number);
for (int j = 0; j < 4; ++j)
{
int x = a + dir[j][0], y = b + dir[j][1];
if (Judge(x, y))
{
swap(NowState[idx], NowState[x * col + y]);//交换
/*int news = cantor(NowState, number);
if (!mark[news])
{
depth = now.depth + 1;
val = CalWeight(NowState, number);
que.push(Node{ ++g_rank, depth, news, val });
v1.push_back(Node{ g_rank, depth, news, val });
mark[news] = 1;
}*/
string newStr = NumToStr(NowState, number);
if (!set1.count(newStr))
{
depth = now.depth + 1;
val = CalWeight(NowState, number);
que.push(Node{ ++g_rank, depth, newStr, val });
v1.push_back(Node{ g_rank, depth, newStr, val });
map1[newStr] = oldStr;
//更新Open表
CString str;
int rows = m_OpenListCtrl.GetItemCount();
str.Format("%d", g_rank);
m_OpenListCtrl.InsertItem(rows, str);
str.Format("%d",depth);
m_OpenListCtrl.SetItemText(rows, 1, str);
str.Format("%d", val + depth);
m_OpenListCtrl.SetItemText(rows, 2, str);
set1.insert(newStr);
}
swap(NowState[idx], NowState[x * col + y]);//恢复交换
}
}
//m_OpenListCtrl.DeleteAllItems();
/*for (int i = 0; i < v1.size(); ++i)
{
CString str;
str.Format("%d", v1[i].rank);
m_OpenListCtrl.InsertItem(0, str);
str.Format("%d", v1[i].depth);
m_OpenListCtrl.SetItemText(0, 1, str);
str.Format("%d", v1[i].val);
m_OpenListCtrl.SetItemText(0, 2, str);
}*/
Node next = que.top();
//decantor(next.cantorVal, NextState, number);
StrToNum(next.str, NextState, number);
if (CalWeight(NextState, number) == 0 && !flag1)
{
flag1 = false;
KillTimer(602);
string str = NumToStr(EndState, number);
while (map1[str] != "-1")
{
v3.push_back(str);
str = map1[str];
}
v3.push_back(str);
//添加最优路径
CString str1;
str1.Format("初始状态: %s", v3.back().c_str());
m_answer.InsertString(0, str1);
str1.Format("目标状态: %s", v3[0].c_str());
m_answer.InsertString(1, str1);
for (int i = v3.size() - 1, j = 2; i > 1; --i, ++j)
{
str1.Format("第%d步:%s->%s", j - 1, v3[i].c_str(), v3[i - 1].c_str());
m_answer.InsertString(j, str1);
}
}
else if (flag1)
{
flag1 = false;
KillTimer(602);
}
Invalidate(FALSE); // 重绘
//KillTimer(602);
/*char str[10];
test(NowState, str, number);
MessageBox(str);
test(NextState, str, number);
MessageBox(str);*/
}
break;
}
CDialog::OnTimer(nIDEvent);
}加快,减慢
//加快
void CEightFigureDlg::OnBnClickedButton1()
{
// TODO: 在此添加控件通知处理程序代码
if (last > 50)
{
last = last - 50;
UpdateData(FALSE);
KillTimer(602);
SetTimer(602, last, NULL);
}
}
//减慢
void CEightFigureDlg::OnBnClickedButton2()
{
// TODO: 在此添加控件通知处理程序代码
if (last < 1000)
{
last = last + 50;
UpdateData(FALSE);
KillTimer(602);
SetTimer(602, last, NULL);
}
}随机生成
打乱数组,使用random_shuffle(),并且判断打乱后的状态是否可解IsSolve()
//随机生成初始状态
void CEightFigureDlg::OnBnClickedRandomButton()
{
// TODO: 在此添加控件通知处理程序代码
flag = false;
random_shuffle(StartState, StartState + number + 1);
while(!IsSolve(StartState, number))
random_shuffle(StartState, StartState + number + 1);
Init();//初始化
for (int i = 0; i <= number; ++i)
{
NowState[i] = NextState[i] = StartState[i];
}
Invalidate(FALSE); // 重绘
}四、参考工程
点击打开链接
五、初充
经博友提醒:发现N数码是否有解写的有问题
需要修改的代码为:
//判断八数码是否有解(初始状态与目标状态的逆序数奇偶性相同)
bool CEightFigureDlg::IsSolve(int *a, int number)
{
int num1, num2;
num1 = inver(a, number);
num2 = inver(EndState, number);
return (num1 % 2) == (num2 % 2);
}需要增加Number奇偶性的判断 参考博客
N为奇数时,初始状态与指定状态逆序数奇偶性相同即有解;N为偶数时,先计算出从初始状态到指定状态,空位要移动的行数m,如果初始状态的逆序数加上m与指定状态的逆序数奇偶性相同,则有解。
代码不在此写了,可以自行修改。