如何使用TensorFlow实现卷积神经网络
作者:黄文坚、唐源
编者按:本文节选自图书《TensorFlow实战》第五章,本书将重点从实用的层面,为读者讲解如何使用TensorFlow实现全连接神经网络、卷积神经网络、循环神经网络,乃至Deep Q-Network。同时结合TensorFlow原理,以及深度学习的部分知识,尽可能让读者通过学习本书做出实际项目和成果。
卷积神经网络简介
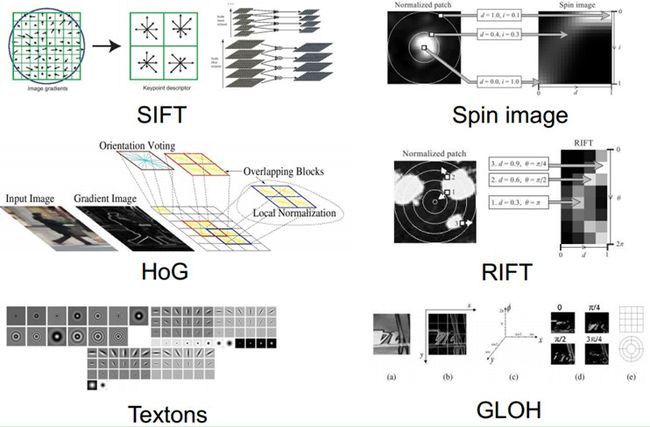
卷积神经网络(Convolutional Neural Network,CNN)最初是为解决图像识别等问题设计的,当然其现在的应用不仅限于图像和视频,也可用于时间序列信号,比如音频信号、文本数据等。在早期的图像识别研究中,最大的挑战是如何组织特征,因为图像数据不像其他类型的数据那样可以通过人工理解来提取特征。在股票预测等模型中,我们可以从原始数据中提取过往的交易价格波动、市盈率、市净率、盈利增长等金融因子,这即是特征工程。但是在图像中,我们很难根据人为理解提取出有效而丰富的特征。在深度学习出现之前,我们必须借助SIFT、HoG等算法提取具有良好区分性的特征,再集合SVM等机器学习算法进行图像识别。如图5-1所示,SIFT对一定程度内的缩放、平移、旋转、视角改变、亮度调整等畸变,都具有不变性,是当时最重要的图像特征提取方法之一。可以说,在之前只能依靠SIFT等特征提取算法才能勉强进行可靠的图像识别。
然而SIFT这类算法提取的特征还是有局限性的,在ImageNet ILSVRC比赛的最好结果的错误率也有26%以上,而且常年难以产生突破。卷积神经网络提取的特征则可以达到更好的效果,同时它不需要将特征提取和分类训练两个过程分开,它在训练时就自动提取了最有效的特征。CNN作为一个深度学习架构被提出的最初诉求,是降低对图像数据预处理的要求,以及避免复杂的特征工程。CNN可以直接使用图像的原始像素作为输入,而不必先使用SIFT等算法提取特征,减轻了使用传统算法如SVM时必需要做的大量重复、烦琐的数据预处理工作。和SIFT等算法类似,CNN训练的模型同样对缩放、平移、旋转等畸变具有不变性,有着很强的泛化性。CNN的最大特点在于卷积的权值共享结构,可以大幅减少神经网络的参数量,防止过拟合的同时又降低了神经网络模型的复杂度。CNN的权值共享其实也很像早期的延时神经网络(TDNN),只不过后者是在时间这一个维度上进行权值共享,降低了学习时间序列信号的复杂度。
卷积神经网络的概念最早出自19世纪60年代科学家提出的感受野(Receptive Field)。当时科学家通过对猫的视觉皮层细胞研究发现,每一个视觉神经元只会处理一小块区域的视觉图像,即感受野。到了20世纪80年代,日本科学家提出神经认知机(Neocognitron)的概念,可以算作是卷积网络最初的实现原型。神经认知机中包含两类神经元,用来抽取特征的S-cells,还有用来抗形变的C-cells,其中S-cells对应我们现在主流卷积神经网络中的卷积核滤波操作,而C-cells则对应激活函数、最大池化(Max-Pooling)等操作。同时,CNN也是首个成功地进行多层训练的网络结构,即前面章节提到的LeCun的LeNet5,而全连接的网络因为参数过多及梯度弥散等问题,在早期很难顺利地进行多层的训练。卷积神经网络可以利用空间结构关系减少需要学习的参数量,从而提高反向传播算法的训练效率。在卷积神经网络中,第一个卷积层会直接接受图像像素级的输入,每一个卷积操作只处理一小块图像,进行卷积变化后再传到后面的网络,每一层卷积(也可以说是滤波器)都会提取数据中最有效的特征。这种方法可以提取到图像中最基础的特征,比如不同方向的边或者拐角,而后再进行组合和抽象形成更高阶的特征,因此CNN可以应对各种情况,理论上具有对图像缩放、平移和旋转的不变性。
一般的卷积神经网络由多个卷积层构成,每个卷积层中通常会进行如下几个操作。
- 图像通过多个不同的卷积核的滤波,并加偏置(bias),提取出局部特征,每一个卷积核会映射出一个新的2D图像。
- 将前面卷积核的滤波输出结果,进行非线性的激活函数处理。目前最常见的是使用ReLU函数,而以前Sigmoid函数用得比较多。
- 对激活函数的结果再进行池化操作(即降采样,比如将2×2的图片降为1×1的图片),目前一般是使用最大池化,保留最显著的特征,并提升模型的畸变容忍能力。
这几个步骤就构成了最常见的卷积层,当然也可以再加上一个LRN(Local Response Normalization,局部响应归一化层)层,目前非常流行的Trick还有Batch Normalization等。
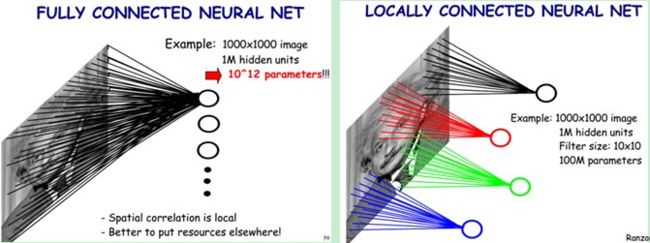
一个卷积层中可以有多个不同的卷积核,而每一个卷积核都对应一个滤波后映射出的新图像,同一个新图像中每一个像素都来自完全相同的卷积核,这就是卷积核的权值共享。那我们为什么要共享卷积核的权值参数呢?答案很简单,降低模型复杂度,减轻过拟合并降低计算量。举个例子,如图5-2所示,如果我们的图像尺寸是1000像素×1000像素,并且假定是黑白图像,即只有一个颜色通道,那么一张图片就有100万个像素点,输入数据的维度也是100万。接下来,如果连接一个相同大小的隐含层(100万个隐含节点),那么将产生100万×100万=一万亿个连接。仅仅一个全连接层(Fully Connected Layer),就有一万亿连接的权重要去训练,这已经超出了普通硬件的计算能力。我们必须减少需要训练的权重数量,一是降低计算的复杂度,二是过多的连接会导致严重的过拟合,减少连接数可以提升模型的泛化性。
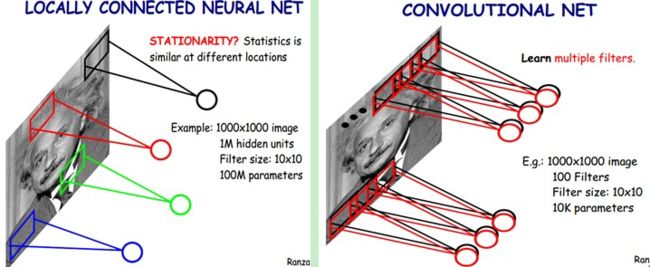
图像在空间上是有组织结构的,每一个像素点在空间上和周围的像素点实际上是有紧密联系的,但是和太遥远的像素点就不一定有什么关联了。这就是前面提到的人的视觉感受野的概念,每一个感受野只接受一小块区域的信号。这一小块区域内的像素是互相关联的,每一个神经元不需要接收全部像素点的信息,只需要接收局部的像素点作为输入,而后将所有这些神经元收到的局部信息综合起来就可以得到全局的信息。这样就可以将之前的全连接的模式修改为局部连接,之前隐含层的每一个隐含节点都和全部像素相连,现在我们只需要将每一个隐含节点连接到局部的像素节点。假设局部感受野大小是10×10,即每个隐含节点只与10×10个像素点相连,那么现在就只需要10×10×100万=1亿个连接,相比之前的1万亿缩小了10000倍。
上面我们通过局部连接(Locally Connect)的方法,将连接数从1万亿降低到1亿,但仍然偏多,需要继续降低参数量。现在隐含层每一个节点都与10×10的像素相连,也就是每一个隐含节点都拥有100个参数。假设我们的局部连接方式是卷积操作,即默认每一个隐含节点的参数都完全一样,那我们的参数不再是1亿,而是100。不论图像有多大,都是这10×10=100个参数,即卷积核的尺寸,这就是卷积对缩小参数量的贡献。我们不需要再担心有多少隐含节点或者图片有多大,参数量只跟卷积核的大小有关,这也就是所谓的权值共享。但是如果我们只有一个卷积核,我们就只能提取一种卷积核滤波的结果,即只能提取一种图片特征,这不是我们期望的结果。好在图像中最基本的特征很少,我们可以增加卷积核的数量来多提取一些特征。图像中的基本特征无非就是点和边,无论多么复杂的图像都是点和边组合而成的。人眼识别物体的方式也是从点和边开始的,视觉神经元接受光信号后,每一个神经元只接受一个区域的信号,并提取出点和边的特征,然后将点和边的信号传递给后面一层的神经元,再接着组合成高阶特征,比如三角形、正方形、直线、拐角等,再继续抽象组合,得到眼睛、鼻子和嘴等五官,最后再将五官组合成一张脸,完成匹配识别。因此我们的问题就很好解决了,只要我们提供的卷积核数量足够多,能提取出各种方向的边或各种形态的点,就可以让卷积层抽象出有效而丰富的高阶特征。每一个卷积核滤波得到的图像就是一类特征的映射,即一个Feature Map。一般来说,我们使用100个卷积核放在第一个卷积层就已经很充足了。那这样的话,如图5-3所示,我们的参数量就是100×100=1万个,相比之前的1亿又缩小了10000倍。因此,依靠卷积,我们就可以高效地训练局部连接的神经网络了。卷积的好处是,不管图片尺寸如何,我们需要训练的权值数量只跟卷积核大小、卷积核数量有关,我们可以使用非常少的参数量处理任意大小的图片。每一个卷积层提取的特征,在后面的层中都会抽象组合成更高阶的特征。而且多层抽象的卷积网络表达能力更强,效率更高,相比只使用一个隐含层提取全部高阶特征,反而可以节省大量的参数。当然,我们需要注意的是,虽然需要训练的参数量下降了,但是隐含节点的数量并没有下降,隐含节点的数量只跟卷积的步长有关。如果步长为1,那么隐含节点的数量和输入的图像像素数量一致;如果步长为5,那么每5×5的像素才需要一个隐含节点,我们隐含节点的数量就是输入像素数量的1/25。
我们再总结一下,卷积神经网络的要点就是局部连接(Local Connection)、权值共享(Weight Sharing)和池化层(Pooling)中的降采样(Down-Sampling)。其中,局部连接和权值共享降低了参数量,使训练复杂度大大下降,并减轻了过拟合。同时权值共享还赋予了卷积网络对平移的容忍性,而池化层降采样则进一步降低了输出参数量,并赋予模型对轻度形变的容忍性,提高了模型的泛化能力。卷积神经网络相比传统的机器学习算法,无须手工提取特征,也不需要使用诸如SIFT之类的特征提取算法,可以在训练中自动完成特征的提取和抽象,并同时进行模式分类,大大降低了应用图像识别的难度;相比一般的神经网络,CNN在结构上和图片的空间结构更为贴近,都是2D的有联系的结构,并且CNN的卷积连接方式和人的视觉神经处理光信号的方式类似。
大名鼎鼎的LeNet5 诞生于1994年,是最早的深层卷积神经网络之一,并且推动了深度学习的发展。从1988年开始,在多次成功的迭代后,这项由Yann LeCun完成的开拓性成果被命名为LeNet5。LeCun认为,可训练参数的卷积层是一种用少量参数在图像的多个位置上提取相似特征的有效方式,这和直接把每个像素作为多层神经网络的输入不同。像素不应该被使用在输入层,因为图像具有很强的空间相关性,而使用图像中独立的像素直接作为输入则利用不到这些相关性。
LeNet5当时的特性有如下几点。
- 每个卷积层包含三个部分:卷积、池化和非线性激活函数
- 使用卷积提取空间特征
- 降采样(Subsample)的平均池化层(Average Pooling)
- 双曲正切(Tanh)或S型(Sigmoid)的激活函数
- MLP作为最后的分类器
- 层与层之间的稀疏连接减少计算复杂度
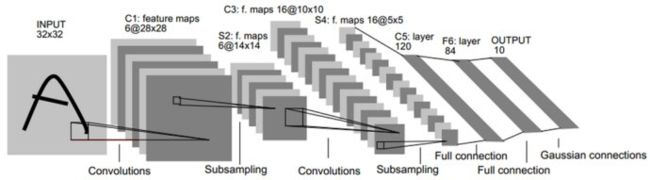
LeNet5中的诸多特性现在依然在state-of-the-art卷积神经网络中使用,可以说LeNet5是奠定了现代卷积神经网络的基石之作。Lenet-5的结构如图5-4所示。它的输入图像为32×32的灰度值图像,后面有三个卷积层,一个全连接层和一个高斯连接层。它的第一个卷积层C1包含6个卷积核,卷积核尺寸为5×5,即总共(5×5+1)×6=156个参数,括号中的1代表1个bias,后面是一个2×2的平均池化层S2用来进行降采样,再之后是一个Sigmoid激活函数用来进行非线性处理。而后是第二个卷积层C3,同样卷积核尺寸是5×5,这里使用了16个卷积核,对应16个Feature Map。需要注意的是,这里的16个Feature Map不是全部连接到前面的6个Feature Map的输出的,有些只连接了其中的几个Feature Map,这样增加了模型的多样性。下面的第二个池化层S4和第一个池化层S2一致,都是2×2的降采样。接下来的第三个卷积层C5有120个卷积核,卷积大小同样为5×5,因为输入图像的大小刚好也是5×5,因此构成了全连接,也可以算作全连接层。F6层是一个全连接层,拥有84个隐含节点,激活函数为Sigmoid。LeNet-5最后一层由欧式径向基函数(Euclidean Radial Basis Function)单元组成,它输出最后的分类结果。
TensorFlow实现简单的卷积网络
本节将讲解如何使用TensorFlow实现一个简单的卷积神经网络,使用的数据集依然是MNIST,预期可以达到99.2%左右的准确率。本节将使用两个卷积层加一个全连接层构建一个简单但是非常有代表性的卷积神经网络,读者应该能通过这个例子掌握设计卷积神经网络的要点。
首先载入MNIST数据集,并创建默认的Interactive Session。本节代码主要来自TensorFlow的开源实现。
from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
sess = tf.InteractiveSession()接下来要实现的这个卷积神经网络会有很多的权重和偏置需要创建,因此我们先定义好初始化函数以便重复使用。我们需要给权重制造一些随机的噪声来打破完全对称,比如截断的正态分布噪声,标准差设为0.1。同时因为我们使用ReLU,也给偏置增加一些小的正值(0.1)用来避免死亡节点(dead neurons)。
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)卷积层、池化层也是接下来要重复使用的,因此也为他们分别定义创建函数。这里的tf.nn.conv2d是TensorFlow中的2维卷积函数,参数中x是输入,W是卷积的参数,比如[5,5,1,32]:前面两个数字代表卷积核的尺寸;第三个数字代表有多少个channel。因为我们只有灰度单色,所以是1,如果是彩色的RGB图片,这里应该是3。最后一个数字代表卷积核的数量,也就是这个卷积层会提取多少类的特征。Strides代表卷积模板移动的步长,都是1代表会不遗漏地划过图片的每一个点。Padding代表边界的处理方式,这里的SAME代表给边界加上Padding让卷积的输出和输入保持同样(SAME)的尺寸。tf.nn.max_pool是TensorFlow中的最大池化函数,我们这里使用2×2的最大池化,即将一个2×2的像素块降为1×1的像素。最大池化会保留原始像素块中灰度值最高的那一个像素,即保留最显著的特征。因为希望整体上缩小图片尺寸,因此池化层的strides也设为横竖两个方向以2为步长。如果步长还是1,那么我们会得到一个尺寸不变的图片。
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1],
padding='SAME')在正式设计卷积神经网络的结构之前,先定义输入的placeholder,x是特征,y_是真实的label。因为卷积神经网络会利用到空间结构信息,因此需要将1D的输入向量转为2D的图片结构,即从1×784的形式转为原始的28×28的结构。同时因为只有一个颜色通道,故最终尺寸为[-1,28,28,1],前面的-1代表样本数量不固定,最后的1代表颜色通道数量。这里我们使用的tensor变形函数是tf.reshape。
x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])
x_image = tf.reshape(x, [-1,28,28,1])接下来定义我们的第一个卷积层。我们先使用前面写好的函数进行参数初始化,包括weights和bias,这里的[5,5,1,32]代表卷积核尺寸为5×5,1个颜色通道,32个不同的卷积核。然后使用conv2d函数进行卷积操作,并加上偏置,接着再使用ReLU激活函数进行非线性处理。最后,使用最大池化函数max_pool_2x2对卷积的输出结果进行池化操作。
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)现在定义第二个卷积层,这个卷积层基本和第一个卷积层一样,唯一的不同是,卷积核的数量变成了64,也就是说这一层的卷积会提取64种特征。
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
因为前面经历了两次步长为2×2的最大池化,所以边长已经只有1/4了,图片尺寸由28×28变成了7×7。而第二个卷积层的卷积核数量为64,其输出的tensor尺寸即为7×7×64。我们使用tf.reshape函数对第二个卷积层的输出tensor进行变形,将其转成1D的向量,然后连接一个全连接层,隐含节点为1024,并使用ReLU激活函数。
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)为了减轻过拟合,下面使用一个Dropout层,Dropout的用法第4章已经讲过,是通过一个placeholder传入keep_prob比率来控制的。在训练时,我们随机丢弃一部分节点的数据来减轻过拟合,预测时则保留全部数据来追求最好的预测性能。
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
最后我们将Dropout层的输出连接一个Softmax层,得到最后的概率输出。
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)我们定义损失函数为cross entropy,和之前一样,但是优化器使用Adam,并给予一个比较小的学习速率1e-4。
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y_conv),
reduction_indices=[1]))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)再继续定义评测准确率的操作,这里和第3章、第4章一样。
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
下面开始训练过程。首先依然是初始化所有参数,设置训练时Dropout的keep_prob比率为0.5。然后使用大小为50的mini-batch,共进行20000次训练迭代,参与训练的样本数量总共为100万。其中每100次训练,我们会对准确率进行一次评测(评测时keep_prob设为1),用以实时监测模型的性能。
tf.global_variables_initializer().run()
for i in range(20000):
batch = mnist.train.next_batch(50)
if i0 == 0:
train_accuracy = accuracy.eval(feed_dict={x:batch[0], y_: batch[1],
keep_prob: 1.0})
print("step %d, training accuracy %g"%(i, train_accuracy))
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})全部训练完成后,我们在最终的测试集上进行全面的测试,得到整体的分类准确率。
print("test accuracy %g"%accuracy.eval(feed_dict={
x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))
最后,这个CNN模型可以得到的准确率约为99.2%,基本可以满足对手写数字识别准确率的要求。相比之前MLP的2%错误率,CNN的错误率下降了大约60%。这其中主要的性能提升都来自于更优秀的网络设计,即卷积网络对图像特征的提取和抽象能力。依靠卷积核的权值共享,CNN的参数量并没有爆炸,降低计算量的同时也减轻了过拟合,因此整个模型的性能有较大的提升。本节我们只实现了一个简单的卷积神经网络,没有复杂的Trick。接下来,我们将实现一个稍微复杂一些的卷积网络,而简单的MNIST数据集已经不适合用来评测其性能,我们将使用CIFAR-10数据集进行训练,这也是深度学习可以大幅领先其他模型的一个数据集。
TensorFlow实现进阶的卷积网络
本节使用的数据集是CIFAR-10,这是一个经典的数据集,包含60000张32×32的彩色图像,其中训练集50000张,测试集10000张。CIFAR-10如同其名字,一共标注为10类,每一类图片6000张。这10类分别是airplane、automobile、bird、cat、deer、dog、frog、horse、ship和truck,其中没有任何重叠的情况,比如automobile只包括小型汽车,truck只包括卡车,也不会在一张图片中同时出现两类物体。它还有一个兄弟版本CIFAR-100,其中标注了100类。这两个数据集是前面章节提到的深度学习之父Geoffrey Hinton和他的两名学生Alex Krizhevsky和Vinod Nair收集的,图片来源于80 million tiny images这个数据集,Hinton等人对其进行了筛选和标注。CIFAR-10数据集非常通用,经常出现在各大会议的论文中用来进行性能对比,也曾出现在Kaggle竞赛而为大家所知。图5-5所示为这个数据集的一些示例。
许多论文中都在这个数据集上进行了测试,目前state-of-the-art的工作已经可以达到3.5%的错误率了,但是需要训练很久,即使在GPU上也需要十几个小时。CIFAR-10数据集上详细的Benchmark和排名在classification datasets results上(http://rodrigob.github.io/are_we_there_yet/build/classification_datasets_results.html)。据深度学习三巨头之一LeCun说,现有的卷积神经网络已经可以对CIFAR-10进行很好的学习,这个数据集的问题已经解决了。本节中实现的卷积神经网络没有那么复杂(根据Alex描述的cuda-convnet模型做了些许修改得到),在只使用3000个batch(每个batch包含128个样本)时,可以达到73%左右的正确率。模型在GTX 1080单显卡上大概只需要几十秒的训练时间,如果在CPU上训练则会慢很多。如果使用100k个batch,并结合学习速度的decay(即每隔一段时间将学习速率下降一个比率),正确率最高可以到86%左右。模型中需要训练的参数约为100万个,而预测时需要进行的四则运算总量在2000万次左右。在这个卷积神经网络模型中,我们使用了一些新的技巧。
- 对weights进行了L2的正则化。
- 如图5-6所示,我们对图片进行了翻转、随机剪切等数据增强,制造了更多样本。
- 在每个卷积-最大池化层后面使用了LRN层,增强了模型的泛化能力。
我们首先下载TensorFlow Models库,以便使用其中提供CIFAR-10数据的类。
git clone https://github.com/tensorflow/models.git
cd models/tutorials/image/cifar10
然后我们载入一些常用库,比如NumPy和time,并载入TensorFlow Models中自动下载、读取CIFAR-10数据的类。本节代码主要来自TensorFlow的开源实现。
import cifar10,cifar10_input
import tensorflow as tf
import numpy as np
import time
接着定义batch_size、训练轮数max_steps,以及下载CIFAR-10数据的默认路径。
max_steps = 3000
batch_size = 128
data_dir = '/tmp/cifar10_data/cifar-10-batches-bin'
这里定义初始化weight的函数,和之前一样依然使用tf.truncated_normal截断的正态分布来初始化权重。但是这里会给weight加一个L2的loss,相当于做了一个L2的正则化处理。在机器学习中,不管是分类还是回归任务,都可能因特征过多而导致过拟合,一般可以通过减少特征或者惩罚不重要特征的权重来缓解这个问题。但是通常我们并不知道该惩罚哪些特征的权重,而正则化就是帮助我们惩罚特征权重的,即特征的权重也会成为模型的损失函数的一部分。可以理解为,为了使用某个特征,我们需要付出loss的代价,除非这个特征非常有效,否则就会被loss上的增加覆盖效果。这样我们就可以筛选出最有效的特征,减少特征权重防止过拟合。这也即是奥卡姆剃刀法则,越简单的东西越有效。一般来说,L1正则会制造稀疏的特征,大部分无用特征的权重会被置为0,而L2正则会让特征的权重不过大,使得特征的权重比较平均。我们使用wl控制L2 loss的大小,使用tf.nn.l2_loss函数计算weight的L2 loss,再使用tf.multiply让L2 loss乘以wl,得到最后的weight loss。接着,我们使用tf.add_to_collection把weight loss统一存到一个collection,这个collection名为“losses”,它会在后面计算神经网络的总体loss时被用上。
def variable_with_weight_loss(shape, stddev, wl):
var = tf.Variable(tf.truncated_normal(shape, stddev=stddev))
if wl is not None:
weight_loss = tf.multiply(tf.nn.l2_loss(var),wl,name='weight_loss')
tf.add_to_collection('losses', weight_loss)
return var
下面使用cifar10类下载数据集,并解压、展开到其默认位置。
cifar10.maybe_download_and_extract()再使用cifar10_input类中的distorted_inputs函数产生训练需要使用的数据,包括特征及其对应的label,这里返回的是已经封装好的tensor,每次执行都会生成一个batch_size的数量的样本。需要注意的是我们对数据进行了Data Augmentation(数据增强)。具体的实现细节,读者可以查看cifar10_input.distorted_inputs函数,其中的数据增强操作包括随机的水平翻转(tf.image.random_flip_left_right)、随机剪切一块24×24大小的图片(tf.random_crop)、设置随机的亮度和对比度(tf.image.random_brightness、tf.image.random_contrast),以及对数据进行标准化tf.image.per_image_whitening(对数据减去均值,除以方差,保证数据零均值,方差为1)。通过这些操作,我们可以获得更多的样本(带噪声的),原来的一张图片样本可以变为多张图片,相当于扩大样本量,对提高准确率非常有帮助。需要注意的是,我们对图像进行数据增强的操作需要耗费大量CPU时间,因此distorted_inputs使用了16个独立的线程来加速任务,函数内部会产生线程池,在需要使用时会通过TensorFlow queue进行调度。
images_train, labels_train = cifar10_input.distorted_inputs(
data_dir=data_dir, batch_size=batch_size)
我们再使用cifar10_input.inputs函数生成测试数据,这里不需要进行太多处理,不需要对图片进行翻转或修改亮度、对比度,不过需要裁剪图片正中间的24×24大小的区块,并进行数据标准化操作。
images_test, labels_test = cifar10_input.inputs(eval_data=True,
data_dir=data_dir,
batch_size=batch_size)
这里创建输入数据的placeholder,包括特征和label。在设定placeholder的数据尺寸时需要注意,因为batch_size在之后定义网络结构时被用到了,所以数据尺寸中的第一个值即样本条数需要被预先设定,而不能像以前一样可以设为None。而数据尺寸中的图片尺寸为24×24,即是裁剪后的大小,而颜色通道数则设为3,代表图片是彩色有RGB三条通道。
image_holder = tf.placeholder(tf.float32, [batch_size, 24, 24, 3])
label_holder = tf.placeholder(tf.int32, [batch_size])
做好了准备工作,接下来开始创建第一个卷积层。先使用之前写好的variable_with_weight_loss函数创建卷积核的参数并进行初始化。第一个卷积层使用5×5的卷积核大小,3个颜色通道,64个卷积核,同时设置weight初始化函数的标准差为0.05。我们不对第一个卷积层的weight进行L2的正则,因此wl(weight loss)这一项设为0。下面使用tf.nn.conv2d函数对输入数据image_holder进行卷积操作,这里的步长stride均设为1,padding模式为SAME。把这层的bias全部初始化为0,再将卷积的结果加上bias,最后使用一个ReLU激活函数进行非线性化。在ReLU激活函数之后,我们使用一个尺寸为3×3且步长为2×2的最大池化层处理数据,注意这里最大池化的尺寸和步长不一致,这样可以增加数据的丰富性。再之后,我们使用tf.nn.lrn函数,即LRN对结果进行处理。LRN最早见于Alex那篇用CNN参加ImageNet比赛的论文,Alex在论文中解释LRN层模仿了生物神经系统的“侧抑制”机制,对局部神经元的活动创建竞争环境,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力。Alex在ImageNet数据集上的实验表明,使用LRN后CNN在Top1的错误率可以降低1.4%,因此在其经典的AlexNet中使用了LRN层。LRN对ReLU这种没有上限边界的激活函数会比较有用,因为它会从附近的多个卷积核的响应(Response)中挑选比较大的反馈,但不适合Sigmoid这种有固定边界并且能抑制过大值的激活函数。
weight1 = variable_with_weight_loss(shape=[5, 5, 3, 64], stddev=5e-2,
wl=0.0)
kernel1 = tf.nn.conv2d(image_holder, weight1, [1, 1, 1, 1], padding='SAME')
bias1 = tf.Variable(tf.constant(0.0, shape=[64]))
conv1 = tf.nn.relu(tf.nn.bias_add(kernel1, bias1))
pool1 = tf.nn.max_pool(conv1, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1],
padding='SAME')
norm1 = tf.nn.lrn(pool1, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75)
现在来创建第二个卷积层,这里的步骤和第一步很像,区别如下。上一层的卷积核数量为64(即输出64个通道),所以本层卷积核尺寸的第三个维度即输入的通道数也需要调整为64;还有一个需要注意的地方是这里的bias值全部初始化为0.1,而不是0。最后,我们调换了最大池化层和LRN层的顺序,先进行LRN层处理,再使用最大池化层。
weight2 = variable_with_weight_loss(shape=[5, 5, 64, 64], stddev=5e-2,
wl=0.0)
kernel2 = tf.nn.conv2d(norm1, weight2, [1, 1, 1, 1], padding='SAME')
bias2 = tf.Variable(tf.constant(0.1, shape=[64]))
conv2 = tf.nn.relu(tf.nn.bias_add(kernel2, bias2))
norm2 = tf.nn.lrn(conv2, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75)
pool2 = tf.nn.max_pool(norm2, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1],
padding='SAME')
在两个卷积层之后,将使用一个全连接层,这里需要先把前面两个卷积层的输出结果全部flatten,使用tf.reshape函数将每个样本都变成一维向量。我们使用get_shape函数,获取数据扁平化之后的长度。接着使用variable_with_weight_loss函数对全连接层的weight进行初始化,这里隐含节点数为384,正态分布的标准差设为0.04,bias的值也初始化为0.1。需要注意的是我们希望这个全连接层不要过拟合,因此设了一个非零的weight loss值0.04,让这一层的所有参数都被L2正则所约束。最后我们依然使用ReLU激活函数进行非线性化。
reshape = tf.reshape(pool2, [batch_size, -1])
dim = reshape.get_shape()[1].value
weight3 = variable_with_weight_loss(shape=[dim, 384], stddev=0.04, wl=0.004)
bias3 = tf.Variable(tf.constant(0.1, shape=[384]))
local3 = tf.nn.relu(tf.matmul(reshape, weight3) + bias3)
接下来的这个全连接层和前一层很像,只不过其隐含节点数下降了一半,只有192个,其他的超参数保持不变。
weight4 = variable_with_weight_loss(shape=[384, 192], stddev=0.04, wl=0.004)
bias4 = tf.Variable(tf.constant(0.1, shape=[192]))
local4 = tf.nn.relu(tf.matmul(local3, weight4) + bias4)
下面是最后一层,依然先创建这一层的weight,其正态分布标准差设为上一个隐含层的节点数的倒数,并且不计入L2的正则。需要注意的是,这里不像之前那样使用softmax输出最后结果,这是因为我们把softmax的操作放在了计算loss的部分。我们不需要对inference的输出进行softmax处理就可以获得最终分类结果(直接比较inference输出的各类的数值大小即可),计算softmax主要是为了计算loss,因此softmax操作整合到后面是比较合适的。
weight5 = variable_with_weight_loss(shape=[192, 10], stddev=1/192.0, wl=0.0)
bias5 = tf.Variable(tf.constant(0.0, shape=[10]))
logits = tf.add(tf.matmul(local4, weight5), bias5)
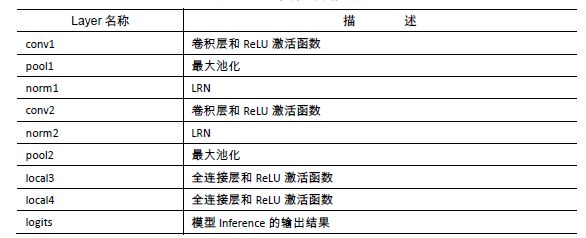
到这里就完成了整个网络inference的部分。梳理整个网络结构可以得到表5-1。从上到下,依次是整个卷积神经网络从输入到输出的流程。可以观察到,其实设计CNN主要就是安排卷积层、池化层、全连接层的分布和顺序,以及其中超参数的设置、Trick的使用等。设计性能良好的CNN是有一定规律可循的,但是想要针对某个问题设计最合适的网络结构,是需要大量实践摸索的。
完成了模型inference部分的构建,接下来计算CNN的loss。这里依然使用cross entropy,需要注意的是我们把softmax的计算和cross entropy loss的计算合在了一起,即tf.nn.sparse_softmax_cross_entropy_with_logits。这里使用tf.reduce_mean对cross entropy计算均值,再使用tf.add_to_collection把cross entropy的loss添加到整体losses的collection中。最后,使用tf.add_n将整体losses的collection中的全部loss求和,得到最终的loss,其中包括cross entropy loss,还有后两个全连接层中weight的L2 loss。
def loss(logits, labels):
labels = tf.cast(labels, tf.int64)
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(
logits=logits, labels=labels, name='cross_entropy_per_example')
cross_entropy_mean = tf.reduce_mean(cross_entropy,
name='cross_entropy')
tf.add_to_collection('losses', cross_entropy_mean)
return tf.add_n(tf.get_collection('losses'), name='total_loss')
接着将logits节点和label_placeholder传入loss函数获得最终的loss。
loss = loss(logits, label_holder)优化器依然选择Adam Optimizer,学习速率设为1e-3。
train_op = tf.train.AdamOptimizer(1e-3).minimize(loss) 使用tf.nn.in_top_k函数求输出结果中top k的准确率,默认使用top 1,也就是输出分数最高的那一类的准确率。
top_k_op = tf.nn.in_top_k(logits, label_holder, 1)使用tf.InteractiveSession创建默认的session,接着初始化全部模型参数。
sess = tf.InteractiveSession()
tf.global_variables_initializer().run()
这一步是启动前面提到的图片数据增强的线程队列,这里一共使用了16个线程来进行加速。注意,如果这里不启动线程,那么后续的inference及训练的操作都是无法开始的。
tf.train.start_queue_runners()现在正式开始训练。在每一个step的训练过程中,我们需要先使用session的run方法执行images_train、labels_train的计算,获得一个batch的训练数据,再将这个batch的数据传入train_op和loss的计算。我们记录每一个step花费的时间,每隔10个step会计算并展示当前的loss、每秒钟能训练的样本数量,以及训练一个batch数据所花费的时间,这样就可以比较方便地监控整个训练过程。在GTX 1080上,每秒钟可以训练大约1800个样本,如果batch_size为128,则每个batch大约需要0.066s。损失loss在一开始大约为4.6,在经过了3000步训练后会下降到1.0附近。
for step in range(max_steps):
start_time = time.time()
image_batch,label_batch = sess.run([images_train,labels_train])
_, loss_value = sess.run([train_op, loss],
feed_dict={image_holder: image_batch, label_holder:label_batch})
duration = time.time() - start_time
if step % 10 == 0:
examples_per_sec = batch_size / duration
sec_per_batch = float(duration)
format_str=('step %d,loss=%.2f (%.1f examples/sec; %.3f sec/batch)')
print(format_str % (step,loss_value,examples_per_sec,sec_per_batch))
接下来评测模型在测试集上的准确率。测试集一共有10000个样本,但是需要注意的是,我们依然要像训练时那样使用固定的batch_size,然后一个batch一个batch地输入测试数据。我们先计算一共要多少个batch才能将全部样本评测完。同时,在每一个step中使用session的run方法获取images_test、labels_test的batch,再执行top_k_op计算模型在这个batch的top 1上预测正确的样本数。最后汇总所有预测正确的结果,求得全部测试样本中预测正确的数量。
num_examples = 10000
import math
num_iter = int(math.ceil(num_examples / batch_size))
true_count = 0
total_sample_count = num_iter * batch_size
step = 0
while step < num_iter:
image_batch,label_batch = sess.run([images_test,labels_test])
predictions = sess.run([top_k_op],feed_dict={image_holder: image_batch,
label_holder:label_batch})
true_count += np.sum(predictions)
step += 1
最后将准确率的评测结果计算并打印出来。
precision = true_count / total_sample_count
print('precision @ 1 = %.3f' % precision)最终,在CIFAR-10数据集上,通过一个短时间小迭代次数的训练,可以达到大致73%的准确率。持续增加max_steps,可以期望准确率逐渐增加。如果max_steps比较大,则推荐使用学习速率衰减(decay)的SGD进行训练,这样训练过程中能达到的准确率峰值会比较高,大致接近86%。而其中L2正则及LRN层的使用都对模型准确率有提升作用,他们都可以从某些方面提升模型的泛化性。
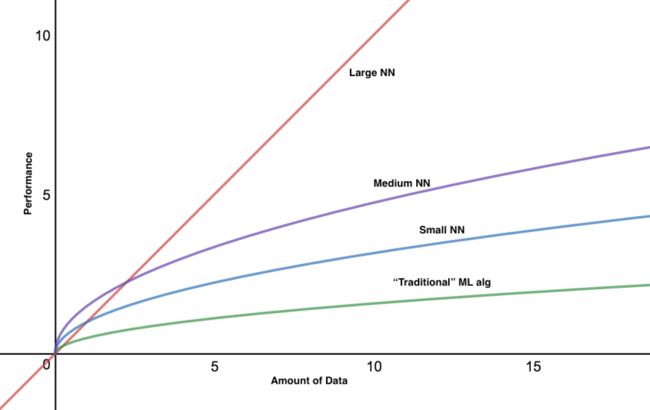
数据增强(Data Augmentation)在我们的训练中作用很大,它可以给单幅图增加多个副本,提高图片的利用率,防止对某一张图片结构的学习过拟合。这刚好是利用了图片数据本身的性质,图片的冗余信息量比较大,因此可以制造不同的噪声并让图片依然可以被识别出来。如果神经网络可以克服这些噪声并准确识别,那么它的泛化性必然会很好。数据增强大大增加了样本量,而数据量的大小恰恰是深度学习最看重的,深度学习可以在图像识别上领先其他算法的一大因素就是它对海量数据的利用效率非常高。用其他算法,可能在数据量大到一定程度时,准确率就不再上升了,而深度学习只要提供足够多的样本,准确率基本可以持续提升,所以说它是最适合大数据的算法。如图5-6所示,传统的机器学习算法在获取了一定量的数据后,准确率上升曲线就接近瓶颈,而神经网络则可以持续上升到更高的准确率才接近瓶颈。规模越大越复杂的神经网络模型,可以达到的准确率水平越高,但是也相应地需要更多的数据才能训练好,在数据量小时反而容易过拟合。我们可以看到Large NN在数据量小的时候,并不比常规算法好,直到数据量持续扩大才慢慢超越了常规算法、Small NN和Medium NN,并在最后达到了一个非常高的准确率。根据Alex在cuda-convnet上的测试结果,如果不对CIFAR-10数据使用数据增强,那么错误率最低可以下降到17%;使用数据增强后,错误率可以下降到11%左右,模型性能的提升非常显著。
从本章的例子中可以发现,卷积层一般需要和一个池化层连接,卷积加池化的组合目前已经是做图像识别时的一个标准组件了。卷积网络最后的几个全连接层的作用是输出分类结果,前面的卷积层主要做特征提取的工作,直到最后的全连接层才开始对特征进行组合匹配,并进行分类。卷积层的训练相对于全连接层更复杂,训练全连接层基本是进行一些矩阵乘法运算,而目前卷积层的训练基本依赖于cuDNN的实现(另有nervana公司的neon也占有一席之地)。其中的算法相对复杂,有些方法(比如Facebook开源的算法)还会涉及傅里叶变换。同时,卷积层的使用有很多Trick,除了本章提到的方法,实际上有很多方法可以防止CNN过拟合,加快收敛速度或者提高泛化性,这些会在后续章节中讲解。
《TensorFlow实战》订购链接:https://item.jd.com/12125568.html 
2017中国人工智能大会(CCAI 2017)由中国人工智能学会、阿里巴巴集团&蚂蚁金服主办,CSDN承办,大会将于7月22日-23日在杭州隆重举行,是年度最专业的AI技术盛宴,40+位实力讲师+8场权威专家主题报告+4场开放式专题研讨会+100多家媒体报道+超过2000位技术精英和专业人士参会,与大牛面对面,官网/报名地址:http://ccai.caai.cn/