1. PCA的原理介绍 (附PCA+SVD原理介绍,PCA+SVD在python下的具体代码实践,python成熟PCA+SVD包的调用,训练集测试集在PCA时注意事项的链接)
好久没更博客了,最近刚做完毕设,打算就用到的方法大概的做几个简介,有些方法网上也有很多简介,但是多多少少我发现都有点不太仔细或者便于理解,今天刚好总结一下这段时间用到的算法之一,然后也算梳理一下思绪。
PCA,SVD原理介绍及python下的具体实现及包的调用
- 1. PCA原理介绍
- 1.1 降维动机与维度灾难
- 1.2 PCA降维理论介绍
- 1.3 PCA降维具体步骤
- 1.3.1 数据预处理:零均值化(必须有)+ 标准化(可有可无)
- 1.3.2 数据预处理后求协方差矩阵:
- 1.3.3 求出协方差矩阵的特征值和特征向量,得到投影矩阵:
- 1.3.4 得出PCA降维后的新样本数据:
- 2. PCA+SVD原理介绍
- 3. python下编写代码实现PCA+SVD
- 4. python里如何使用成熟的现有PCA包
1. PCA原理介绍
写在前面:
如果还没看过PCA的例程的话,可以先去看看示例,看完示例后再来看本文的理论推导,一定会看懂PCA的!
PCA示例:主成分分析(PCA)一次讲个够
但由于我才疏学浅,只能讲一些PCA入门基本掌握知识,不能讲出什么很深的东西,但是用来理解PCA,入门PCA是没问题的~
1.1 降维动机与维度灾难
先说说机器学习里面的降维的动机。降维的动机主要是来源于 维度灾难 , 一般我们为了获得更好的分类精度,会选择增加一些特征,但是当特征数量达到一定数量后,增加特征不光不能提高分类精度反而导致分类精度的下降。或者有些特征与最终精度的关系很小,加入新的特征会增加冗余,却不能提高精度。所谓维灾难就是随着特征维度的增加计算开销急剧增加,而分类精度下降(或者聚类质量下降)。这次提到的PCA是一种典型的无监督线性降维方法。
1.2 PCA降维理论介绍
PCA将数据投射到一个低维子空间实现降维。例如,二维数据集降维就是把点投射成一条线,数据集的每个样本都可以用一个值表示,不需要两个值。三维数据集可以降成二维,就是把变量映射成一个平面。一般情况下,n维数据集可以通过映射降成k维子空间,其中k是选取的主成分数目。 主成分是原始数据集的属性集合乘以一个投影矩阵得到的,所以主成分不一定只有一个,而是由原始数据集的属性集合通过矩阵变换形成的新的属性集合。
↓
那么怎么选择主成分呢?
↓
来看下面这张图作为一个简单的引入例:

数据集看起来像一个从原点到右上角延伸的细长扁平的椭圆。要降低整个数据集的维度,我们必须把点映射成一条线。下图中的两条线(红线+蓝线,红线垂直蓝线)都是数据集可以映射的,映射到哪条线样本变化最大?

一般来说, 方差大的方向是信号的方向,方差小的方向是噪声的方向 ,我们在数据挖掘中或者数字信号处理中,往往要提高信号与噪声的比例,也就是信噪比。
方差计算公式: 方差是各个样本与样本均值的差的平方和的均值:

显然,样本映射到蓝线的变化比映射到红线的变化大,即到 原点的距离大,距离用方差衡量,即方差大,即尽可能的在这个方向上展现了点和点之间的区别,相当于祛除了一些其他方向的噪声,从一个方向也能清晰地分别点和点,则点在这个方向的投影 (点垂直蓝线做一条线,线与蓝线相交的点) 就变成了这个方向上新的点。对上图来说,如果我们只保留蓝线方向的数据,也可以对原数据进行不错的近似了。
如果我们把这些点单纯的投影到x轴或者y轴上,最后在x轴与y轴上得到的方差是相似的(因为这些点的趋势是在45度左右的方向,所以投影到x轴或者y轴上都是类似的),如果我们使用原来的xy坐标系去看这些点,容易看不出来这些点真正的方向是什么。但是如果我们 进行坐标系的变化,横轴变成了蓝线的方向,纵轴变成了红线的方向 ,则就很容易发现什么方向的方差大,什么方向的方差小了。
↓
实际上,这条蓝线就是第一主成分,那如何找第二个主成分呢?
↓
第二主成分必须与第一主成分正交,也就是说第二主成分必须是在统计学上独立的, 每一个主成分需要和前面的主成分正交且尽量多的保留剩下的变量。
所以与蓝线正交的平面上使得变量到新坐标系原点距离最大的投影主成分方向为 红线方向, 即红线方向是第二主成分方向。
第三个主方向是在与第1、2个主方向正交的平面中方差最大,以此类推…
以下为从方差转为极大值问题的角度来理解PCA PCA和SVD傻傻分不清楚?

数据在 w 方向上的投影为 z=w T ^T Tx,我们希望数据点在新的空间中保留最大的差异性即方差最大,所以:
希望 var(z)=w T ^T T∑w 最大化,其中 ∑=cov(x),||w||=1。 根据拉格朗日:
max w _w w w T ^T T∑w−α(w T ^T Tw−1)
关于 w 求导得:
2∑−2αw=0 ⇒ ∑w=αw 其中α 就是特征值,w 就是特征向量。
所以只需对协方差矩阵 ∑ 进行特征值分解,将求得的特征值排序:λ1≥λ2≥…≥λn,再取前k个特征值对应的特征向量构成W=(w1,w2,…,wk),就是主成分分析的解。
此外,andrew ng ML视频里PCA的那一节也有详细推导:
我整理后大概如下:

1.3 PCA降维具体步骤
1.3.1 数据预处理:零均值化(必须有)+ 标准化(可有可无)
a. 零均值化
首先得到原先样本集合每属性 那 一列 所有样本的的均值,零均值化就是样本集合的每一列所有样本都减去对应这一列的均值。使得每个属性那一列的均值为0;
b.标准化(无量纲化)
在进行特征选择之前,一般会先进行数据无量纲化处理,这样,表征不同属性(单位不同)的各特征之间才有可比性,如1cm 与 0.1kg 你怎么比?无量纲处理方法很多,使用不同的方法,对最终的机器学习模型会产生不同的影响。 目前有三种常见的去量纲方法:(1)min-max归一化(2)z-score标准化(3)Normalization;
去量纲方法的具体介绍见:
PCA填坑篇——使用PCA到底需不需要数据去量纲?
数据预处理之数据无量纲化(标准化/归一化)
PCA用到的去量纲方法就是对零均值化后的数据进行 z-score 标准化处理。
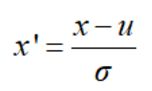
x是原始数据,u是样本均值,σ是样本标准差。(这里因为已经经过了零均值化,所以U=0,z-score就是把标准差归一化和零均值化综合在一起了!)
回顾下正态分布的基本性质,若x~N(u,σ^2),则有:

于是,可以看出,z-score标准化方法试图将原始数据集标准化成均值为0,方差为1且接近于标准正态分布的数据集。然而,一旦原始数据的分布不接近于一般正态分布,则标准化的效果会不好。 该方法比较适合数据量大的场景(即样本足够多,现在都流行大数据,因此可以比较放心地用)。
z-score 该方法不仅能够去除量纲, 还能够把所有维度的变量一视同仁(因为每个维度都服从均值为0、方差1的正态分布),在最后计算距离时各个维度数据发挥了相同的作用 ,避免了不同量纲的选取对距离计算产生的巨大影响。
1.3.2 数据预处理后求协方差矩阵:
a. 协方差(Covariance):
协方差是度量两个变量的变动的同步程度,也就是度量两个变量线性相关性程度。
如果两个变量的协方差为0,则统计学上认为二者线性无关。注意两个无关的变量并非完全独立,只是没有线性相关性而已
如果协方差不为0,如果大于0表示正相关,小于0表示负相关。
当协方差大于0时,一个变量增大是另一个变量也会增大。
当协方差小于0时,一个变量增大是另一个变量会减小。
协方差计算公式如下:

b. 协方差矩阵 :协方差矩阵就是一个数据集里变量两两之间协方差所组成的,它肯定是一个方阵,行是属性节点集合,列和行节点顺序一样。矩阵对角线上即属性自身的方差,C.矩阵的第 (i,j) 个元素是数据集中第i和第j个元素的协方差。(i≠j)
1.3.3 求出协方差矩阵的特征值和特征向量,得到投影矩阵:
特征向量和特征值只能由方阵得出,且并非所有方阵都有特征向量和特征值。
如果一个矩阵有特征向量和特征值,那么它的每个维度(特征)都有一对特征向量和特征值。
特征向量特征值求解如下式:
![]()
( υ \upsilon υ是特征向量,A是协方差矩阵,它是一个方阵; λ \lambda λ是特征值。)
具体如何求解特征值特征向量的过程详见线性代数,在此不多过赘述。
将协方差矩阵按照特征值大小排序特征向量,得到特征向量为 每列 组成的矩阵,从大到小取前K个特征值对应的特征向量作为列组成投影矩阵P。
1.3.4 得出PCA降维后的新样本数据:
如果我们要把5维数据降成3维,那么我们就要用一个3维矩阵做投影矩阵。
我们用数据矩阵点乘投影矩阵。将原先m * n的样本矩阵A (不是上面的协方差矩阵)变换成一个m * r的样本矩阵B,这样就会使得本来有n个feature的A,变成了有r个feature的B(r < n),这r个其实就是对n个feature的A的一种提炼,我们就把这个称为feature的压缩。用数学语言表示就是:
![]()

样本矩阵B就是PCA降维后的新矩阵。
如果你到这里都成功理解了,恭喜你基本看懂了PCA!因为到此,PCA降维完毕!
现在很多都是通过引入SVD综合PCA,来对PCA进行优化,但是PCA怎么和SVD扯上关系呢?
↓
2. PCA+SVD原理介绍
见我的另一篇博客: PCA+SVD原理介绍
3. python下编写代码实现PCA+SVD
见我的另一篇博客:python下编写代码实现PCA+SVD
4. python里如何使用成熟的现有PCA包
见我的另一篇博客:python里如何使用成熟的现有PCA包