图
图是由一些小圆点(称为顶点)和连接这些小圆点的直线(称为边)组成的。
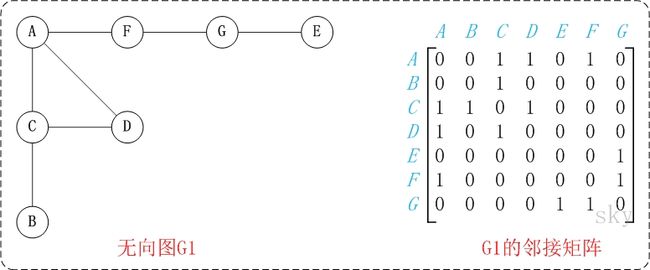
无向图
无向图用矩阵表示的时候会发现中间是沿着对角线对称的。
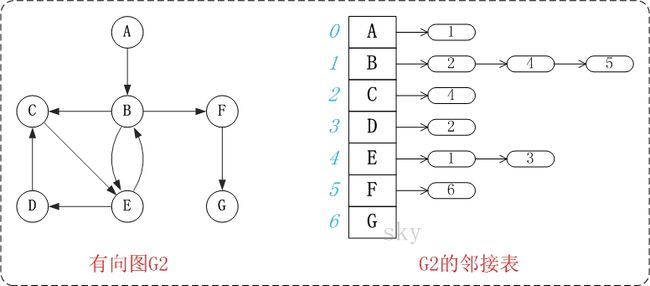
有向图
使用深度优先搜索遍历图
方式
把图的每一个顶点都访问一次。
输入
5 8
1 2
1 5
2 3
2 5
3 1
3 4
4 5
5 3无向图
#include
int e[100][100], book[100], n, sum = 0;
void dfs(int cur) {
int i;
printf("%d ", cur);
sum++;
// 边界
if (sum == n) {
return;
}
// 尝试每一步
for (i = 1; i <=n; i++) {
if (e[cur][i] == 1 && book[i] == 0) {
book[i] = 1;
dfs(i);
}
}
}
int main(void) {
int i, j, m, a, b;
scanf("%d %d", &n, &m);
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
if (i == j) e[i][j] = 0;
else e[i][j] = 9;
// 二位数组是沿着主对角线对称,即无向图
for (i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
e[a][b] = 1;
e[b][a] = 1;
}
book[1] = 1;
dfs(1);
printf("\n");
for (i = 1; i <= n; i++) {
for (j = 1; j <= n; j++) {
printf("%5d ", e[i][j]);
}
printf("\n");
}
return 0;
} 有向图
#include
int e[100][100], book[100], n, sum = 0;
void dfs(int cur) {
int i;
printf("%d ", cur);
sum++;
// 边界
if (sum == n) {
return;
}
// 尝试每一步
for (i = 1; i <=n; i++) {
if (e[cur][i] == 1 && book[i] == 0) {
book[i] = 1;
dfs(i);
}
}
}
int main(void) {
int i, j, m, a, b;
scanf("%d %d", &n, &m);
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
if (i == j) e[i][j] = 0;
else e[i][j] = 9;
// 二位数组是沿着主对角线对称,即无向图
for (i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
e[a][b] = 1;
}
book[1] = 1;
dfs(1);
printf("\n");
for (i = 1; i <= n; i++) {
for (j = 1; j <= n; j++) {
printf("%5d ", e[i][j]);
}
printf("\n");
}
return 0;
} 使用广度优先搜索遍历图
方式
首先以一个未被访问过的顶点作为起始顶点,然后将与顶点相邻的未访问过的顶点依次再放入队列中。
输入
5 8
1 2
1 5
2 3
2 5
3 1
3 4
4 5
5 3无向图
#include
int main(void) {
int e[100][100], book[100] = {0}, n, sum = 0;
int i, j, m, a, b, cur;
// 初始化队列
struct node {
int n;
} que[100];
int head = 0;
int tail = 0;
scanf("%d %d", &n, &m);
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
if (i == j) e[i][j] = 0;
else e[i][j] = 9;
// 二位数组是沿着主对角线对称,即无向图
for (i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
e[a][b] = 1;
e[b][a] = 1;
}
book[1] = 1;
que[tail].n = 1;
tail++;
while (head < tail) {
cur = que[head].n;
for (i = 1; i <= n; i++) {
if (e[cur][i] == 1 && book[i] == 0) {
book[i] = 1;
que[tail].n = i;
tail++;
}
if (tail > n) {
break;
}
}
head++;
}
for (i = 0; i < tail; i++)
printf("%d ", que[i].n);
return 0;
} 有向图
#include
int main(void) {
int e[100][100], book[100] = {0}, n, sum = 0;
int i, j, m, a, b, cur;
// 初始化队列
struct node {
int n;
} que[100];
int head = 0;
int tail = 0;
scanf("%d %d", &n, &m);
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
if (i == j) e[i][j] = 0;
else e[i][j] = 9;
// 二位数组是沿着主对角线对称,即无向图
for (i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
e[a][b] = 1;
}
book[1] = 1;
que[tail].n = 1;
tail++;
while (head < tail) {
cur = que[head].n;
for (i = 1; i <= n; i++) {
if (e[cur][i] == 1 && book[i] == 0) {
book[i] = 1;
que[tail].n = i;
tail++;
}
if (tail > n) {
break;
}
}
head++;
}
for (i = 0; i < tail; i++)
printf("%d ", que[i].n);
return 0;
} 城市地图-图的深度优先遍历
题目
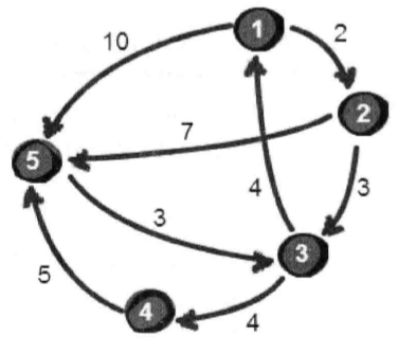
暑假小哼想到去小哈家里去玩,小哼和小哈住在不同的城市,并且小哼之前从来没有去过小哈家,这是小哼第一次上门。怎么办呢?小哼便想起了百度地图。百度地图一下子就给出了从小哼家到小哈家的最短行车方案。爱思考的小哼想知道百度地图是如何计算出最短行车距离的。下面是城市的地图:
代码实现
输入:
5 8
1 2 2
1 5 10
2 3 3
2 5 7
3 1 4
3 4 4
4 5 5
5 3 3最后输出结果:
7无向图版本:
#include
int e[100][100], book[100], n, min = 99999;
void dfs(int cur, int dis) {
int i;
// 边界
if (dis > min) {
return;
}
if (cur == n) {
if (dis < min) {
min = dis;
}
return;
}
// 尝试每一步
for (i = 1; i <=n; i++) {
if (e[cur][i] != 99999999 && book[i] == 0) {
book[i] = 1;
dfs(i, dis + e[cur][i]);
book[i] = 0;
}
}
}
int main(void) {
int i, j, m, a, b, c;
scanf("%d %d", &n, &m);
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
if (i == j) e[i][j] = 0;
else e[i][j] = 99999999;
for (i = 1; i <= m; i++) {
scanf("%d %d %d", &a, &b, &c);
e[a][b] = c;
e[b][a] = c;
}
book[1] = 1;
dfs(1, 0);
printf("%d\n", min);
return 0;
} 有向图版本最后输出结果:
9有向图版本:注释e[b][a] = c;。
最少转机-图的广度优先遍历
题目
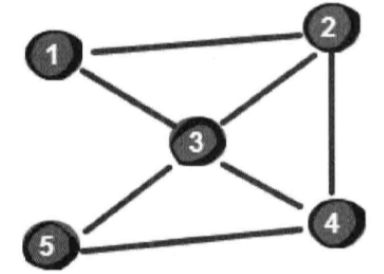
小哼和小哈一同坐飞机去旅游。他们现在位于 1 号城市,目标是 5 号城市,可是 1 号城市并没有到 5 号城市的直航。不过小哼已经收集了很多航班的信息,现在小哼希望找到一种乘坐方式,使得转机的次数最少,如何解决呢?
为什么不能使用深度优先搜索
因为使用深度优先搜索会把图的每一个顶点都访问一次。而题目只需要访问 1 点到 5 点的距离。
代码实现
输入:
5 7 1 5
1 2
1 3
2 3
2 4
3 4
3 5
4 5最后输出结果:
2#include
int main(void) {
int e[100][100], book[100] = {0}, n, sum = 0;
int i, j, m, a, b, c, d, cur;
// 初始化队列
struct node {
int n;
int s;
} que[100];
int head = 0;
int tail = 0;
scanf("%d %d %d %d", &n, &m, &c, &d);
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
if (i == j) e[i][j] = 0;
else e[i][j] = 9;
// 二位数组是沿着主对角线对称,即无向图
for (i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
e[a][b] = 1;
e[b][a] = 1;
}
book[1] = 1;
que[tail].n = 1;
tail++;
while (head < tail) {
cur = que[head].n;
for (i = 1; i <= n; i++) {
if (e[cur][i] == 1 && book[i] == 0) {
book[i] = 1;
que[tail].n = i;
que[tail].s += que[head].s + 1;
tail++;
}
if (que[tail - 1].n == d) {
break;
}
}
head++;
}
printf("%d\n", que[tail - 1].s);
return 0;
}