立体匹配(Stereo Matching)
-
-
-
- 模块类图结构
- BM(Block Matching)
- 1. 参考资料
- 2. 主要公式和概念
- 3. 算法流程
- 4. 注意事项
- SGBM(Semi-Global Block Matching)
- 1. 参考资料
- 2. 主要公式和概念
- 3. 算法流程
- 4. 注意事项
- 重要API参数解析
- 1. StereoBinaryBM
- 2. StereoBinarySGBM
- 一些使用该模块时的注意事项
- 运行效果截图
-
-
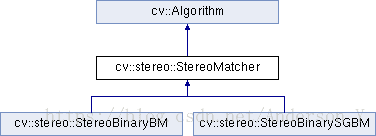
模块类图结构
1. StereoMatcher 类为该模块顶级父类,为一抽象类,定义了StereoBinary*子类的一些公共接口
2. StereoBinaryBM 和 StereoBinarySGBM为StereoMatcher类的两个派生子类, 分别实现了基于BM(Block Matching) 和 SGM(Semi-Global Matching)的立体匹配算法.
BM(Block Matching)
1. 参考资料
(1) Small Vision Systems: Hardware and Implementation 1997
(2) Weighted Semi-Global Matching and Center-Symmetric Census Transform for Robust Driver Assistance 2013
(3) Sum of Absolute Differences algorithm in stereo correspondence problem for stereo matching in computer vision application
2. 主要公式和概念
(0) 一些假设:
块匹配假设在像素的局部区域, 所有像素具有同一视差值.
(1) Census Transformation(CT)变换: 一种将像素值变为Binary String 的变换. 通过将中心像素值与邻域内像素值比较(此处以8邻域为例), 大于中心像素值的置0(1), 反之置1(0). 公式如下:
LBPN(x,y)=∑i=0N−1s(ni−nc)2i>(1) (1) L B P N ( x , y ) = ∑ i = 0 N − 1 s ( n i − n c ) 2 i >
s(x)={10x≥0x<0>> s ( x ) = { 1 x ≥ 0 0 x < 0 > >(2) 计算对应像素点间不同视差值下的汉明距离:
h(x,y,d)=HammingDistance(LBPL(x,y),LBPR(x−d,y))>(2a) (2a) h ( x , y , d ) = H a m m i n g D i s t a n c e ( L B P L ( x , y ) , L B P R ( x − d , y ) ) >
Note: OpenCV的 hammingDistanceBlockMatching() 函数返回的汉明距离图的内存组织形式如下:
Size(hammingDistance)=H×(W∗numDisparities)>(2b) (2b) S i z e ( h a m m i n g D i s t a n c e ) = H × ( W ∗ n u m D i s p a r i t i e s ) >
其中每一行内容如下(以第 i i 行为例, n=numDisparities n = n u m D i s p a r i t i e s ):
| P(0, i) | P(1, i) | … | P(w, i) |
|---|---|---|---|
| h(0,i,0) h ( 0 , i , 0 ) , h(0,i,1) h ( 0 , i , 1 ) , …, h(0,i,n) h ( 0 , i , n ) | h(1,i,0) h ( 1 , i , 0 ) , h(1,i,1) h ( 1 , i , 1 ) ), …, h(1,i,n) h ( 1 , i , n ) | … | h(w−1,i,0) h ( w − 1 , i , 0 ) , h(w−1,i,1) h ( w − 1 , i , 1 ) , …, h(w−1,i,n) h ( w − 1 , i , n ) |
(3) 块代价聚集(Block Cost Aggregate)
OpenCV实现中,分两步实现块代价聚集.
(i) 计算代价累计图
代价的水平积累:
c′(x,y,d)=h(x−1,y−1,d)+c′(x−1,y,d)>(3.1a) (3.1a) c ( x , y , d ) ′ = h ( x − 1 , y − 1 , d ) + c ( x − 1 , y , d ) ′ >
代价的垂直积累:
c(x,y,d)=c′(x,y,d)+c′(x,y−1,d)>(3.1b) (3.1b) c ( x , y , d ) = c ( x , y , d ) ′ + c ( x , y − 1 , d ) ′ >
(ii) 根据代价累计图计算指定窗内的块聚集代价
C(x,y,d)=c(x−w,y−w,d)+c(x+w,y+w,d)−c(x−w,y+w,d)−c(x+w,y−w,d)>(3.2) (3.2) C ( x , y , d ) = c ( x − w , y − w , d ) + c ( x + w , y + w , d ) − c ( x − w , y + w , d ) − c ( x + w , y − w , d ) >
其中 w=(windowSize/2) w = ( w i n d o w S i z e / 2 ) windowSize w i n d o w S i z e 必须为奇数. 上面两步的操作实际上就是求以某一点为中心的一个局部窗内的像素点的汉明距离的和. (4) 根据块聚集代价图计算视差图
(i) 在上一步得到的 C(x,y,d) C ( x , y , d ) 图中, 在每一个像素处,假设存在一个以像素 p(x,y) p ( x , y ) 为横轴,以视差 d d 为纵轴的局部坐标系 Coor(p,d) C o o r ( p , d ) :
首先在坐标平面 Coor(p,d) C o o r ( p , d ) 内原点处,沿垂直方向搜索一点 (0,lr) ( 0 , l r ) 使得该点的 C(x,y,d) C ( x , y , d ) 值最小且满足confidence check条件(其中 min∗ m i n ∗ 表示第几小):
lr={min3(C(x,y,d3))min1(C(x,y,d1))≤CONFIDENCE,−1,d1others>(4.1a) (4.1a) l r = { m i n 3 ( C ( x , y , d 3 ) ) m i n 1 ( C ( x , y , d 1 ) ) ≤ C O N F I D E N C E , d 1 − 1 , o t h e r s >
当 lr≠−1 l r ≠ − 1 时, 再次在坐标平面 Coor(p,d) C o o r ( p , d ) 内的 [p−lr,pnumDisparity−lr] [ p − l r , p n u m D i s p a r i t y − l r ] 区间内沿对角线搜索一点 (p,v) ( p , v ) 使得该点同样满足上述条件:
v={min3(C(x,y,d3))min1(C(x,y,d1))≤CONFIDENCE,−1,d1others>(4.1b) (4.1b) v = { m i n 3 ( C ( x , y , d 3 ) ) m i n 1 ( C ( x , y , d 1 ) ) ≤ C O N F I D E N C E , d 1 − 1 , o t h e r s >
(ii) 得到 lr,v l r , v 后, 对其进行差值,得到sub-pixel级别的结果 p1,p2 p 1 , p 2 , 如果 p1,p2 p 1 , p 2 差值在阈值范围内,则该像素点的视差值为 p2∗scallingFactor p 2 ∗ s c a l l i n g F a c t o r , 否则视差为0:p1,p2 p 1 , p 2 差值公式如下:
p′={12−14∗[(m3−m1m2−m1)2+m3−m1m2−m1]−1∗[12−14∗[(m3−m1m2−m1)2+m3−m1m2−m1]]m2>m3others>(4.2.a) (4.2.a) p ′ = { 1 2 − 1 4 ∗ [ ( m 3 − m 1 m 2 − m 1 ) 2 + m 3 − m 1 m 2 − m 1 ] m 2 > m 3 − 1 ∗ [ 1 2 − 1 4 ∗ [ ( m 3 − m 1 m 2 − m 1 ) 2 + m 3 − m 1 m 2 − m 1 ] ] o t h e r s >
p1=p′+v>(4.2.b) (4.2.b) p 1 = p ′ + v >
p2=p′+lr>(4.2.c) (4.2.c) p 2 = p ′ + l r >
d={p2∗scallingFactor0|p1−p2|≤threshothers>(4.2.d) (4.2.d) d = { p 2 ∗ s c a l l i n g F a c t o r | p 1 − p 2 | ≤ t h r e s h 0 o t h e r s > Note: 计算 p1,p2 p 1 , p 2 时, p′ p ′ 计算公式中的 m1,m2,m3 m 1 , m 2 , m 3 是不相同的.
(5) 后处理: 滤掉一些斑点区域(speckle)同时对于空洞区域进行插值处理.
CV_SPECKLE_REMOVAL_AVG_ALGORITHMd(x,y)={d(x,y)1n(∑nid(xi,yi))d(x,y)>0others>(5a) (5a) C V _ S P E C K L E _ R E M O V A L _ A V G _ A L G O R I T H M d ( x , y ) = { d ( x , y ) d ( x , y ) > 0 1 n ( ∑ i n d ( x i , y i ) ) o t h e r s >
CV_SPECKLE_REMOVAL_ALGORITHMd(x,y)={d(x,y)NEW_VALUEd(x,y)>0others>(5b) (5b) C V _ S P E C K L E _ R E M O V A L _ A L G O R I T H M d ( x , y ) = { d ( x , y ) d ( x , y ) > 0 N E W _ V A L U E o t h e r s >
3. 算法流程
4. 注意事项
(1) 通过create() 创建BM算法对象时, numDisparities 参数必须能被16整除, blockSize 参数必须为奇数.
(2) 通过compute() 函数计算视差图时, 作为输入参数的左右两张图必须具有相同大小且图像类型都为CV_8UC1.
SGBM(Semi-Global Block Matching)
1. 参考资料
(1) Stereo Processing by Semi-Global Matching and Mutual Information 2008
(2) A Pixel Dissimilarity Measure That Is Insensitive to Image Sampling 1998
(3) Small Vision Systems: Hardware and Implementation 1997
2. 主要公式和概念
(0) 一些基本公式
MII1,I2=H1+H2−HI1,I2>(1) (1) M I I 1 , I 2 = H 1 + H 2 − H I 1 , I 2 >
HI=−∫10PI(i)logPI(i)di>(2) (2) H I = − ∫ 0 1 P I ( i ) l o g P I ( i ) d i >
HI1,I2=−∫10∫10PI1,I2(i1,i2)logPI1,I2(i1,i2)di1di2>(3) (3) H I 1 , I 2 = − ∫ 0 1 ∫ 0 1 P I 1 , I 2 ( i 1 , i 2 ) l o g P I 1 , I 2 ( i 1 , i 2 ) d i 1 d i 2 >
HI1,I2=∑phI1,I2(I1p,I2p)>(4) (4) H I 1 , I 2 = ∑ p h I 1 , I 2 ( I 1 p , I 2 p ) >
hI1,I2(i,k)=−1nlog(PI1,I2(i,k)⊗g(i,k))⊗g(i,k)>(5) (5) h I 1 , I 2 ( i , k ) = − 1 n l o g ( P I 1 , I 2 ( i , k ) ⊗ g ( i , k ) ) ⊗ g ( i , k ) >
PI1,I2(i,k)=1n∑pT[(i,k)==(I1p,I2p)]>(6) (6) P I 1 , I 2 ( i , k ) = 1 n ∑ p T [ ( i , k ) == ( I 1 p , I 2 p ) ] > (1) Mutual Information(互信息):
参考:
博客: 经典算法Semi-Global Matching(SGM) 之HMI计算
MI是一种基于熵定义的用于表示两幅图相关性的一个概念. 对于在Base Image 和 Match Image 中没有相互对应的像素点对的值 I1,I2 I 1 , I 2 ,对其熵的定义仿照联合熵进行定义:
HI=∑phI(Ip)>(1a) (1a) H I = ∑ p h I ( I p ) >
hI(i)=−1nlog(PI(i)⊗g(i))⊗g(i)>(1b) (1b) h I ( i ) = − 1 n l o g ( P I ( i ) ⊗ g ( i ) ) ⊗ g ( i ) >其中 g(i) g ( i ) 为 Gaussian 函数。
因此, MI 的最总定义如下:
MII1,I2=∑pmiIi,I2(I1p,I2p)>(1c) (1c) M I I 1 , I 2 = ∑ p m i I i , I 2 ( I 1 p , I 2 p ) >
miIi,I2(i,k)=hI1(i)+hI2(k)−hI1,I2(i,k)>(1d) (1d) m i I i , I 2 ( i , k ) = h I 1 ( i ) + h I 2 ( k ) − h I 1 , I 2 ( i , k ) > (2) 基于MI的代价函数(MI Matching Cost) CMI C M I :
CMI(p,d)=−miIb,fD(Im)(Ibp,Imq)>(2a) (2a) C M I ( p , d ) = − m i I b , f D ( I m ) ( I b p , I m q ) >
q=ebm(p,d)>(2b) (2b) q = e b m ( p , d ) >
>ebm(p,d)=[px−d,py]T>(2c) (2c) > e b m ( p , d ) = [ p x − d , p y ] T >
fD(Im)=D+Im> f D ( I m ) = D + I m >其中 D D 为视差图 D=Ib−Im D = I b − I m
Note: 根据上述公式定义,可以看到, CMI C M I 的计算需要事先知道视差图。这在实际应用中是不太可能满足的。作者在论文中提出了,首先对原图进行 116 1 16 的缩放,然后初始化一张随机的视差图,进行3次迭代计算后,再逐层向上放大,每层进行一次计算,直到和原图大小相同为止。另外,需要注意,为了保证误差不会逐层向上传播,较低分辨率的视差图只用于估计 P P ,而 CMI C M I 则用更高分辨率的视差图进行计算,其余的所有参数都从0开始计算. 上述公式中, (i,k) ( i , k ) 分别代表 I1,I2 I 1 , I 2 中像素点的值(pixel intensities)。 PI(i) P I ( i ) 和 PI1.I2(i,k) P I 1 . I 2 ( i , k ) 表示值为 i i 的像素点和 (i,k) ( i , k ) 的像素点对出现的概率。
(3) 代价聚集(Cost Aggregation)
参考:
博客: 经典算法Semi-Global Matching(SGM) 之动态规划
首先定义全局能量函数:
E(D)=∑p[C(p,Dp)+∑q∈Np(P1T[|Dp−Dq|=1])+∑q∈Np(P2T[|Dp−Dq|>1])]>(11) (11) E ( D ) = ∑ p [ C ( p , D p ) + ∑ q ∈ N p ( P 1 T [ | D p − D q | = 1 ] ) + ∑ q ∈ N p ( P 2 T [ | D p − D q | > 1 ] ) ] >
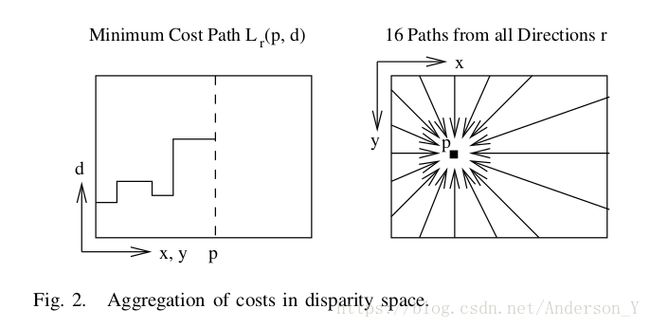
其中 Np N p 表示像素 p p 的邻域. P1,P2 P 1 , P 2 是惩罚系数.较小的 P1 P 1 使得该能量函数对于斜面和曲面(slanted or curved surface) 具有一定的适应性, 较大的 P2 P 2 使得能量函数能尽量阻止不连续性视差的产生. 一般来说,在边缘处的视差不连续变换是正常的,因此可以将 P2 P 2 设置为一个与图像梯度相适应的值,即 P2=P′2|Ibp−Ibq| P 2 = P 2 ′ | I b p − I b q | .这样,对于处于边缘处的像素,即使是较大的视差变化,也能容忍. 有了上述能量函数后,求解立体匹配的问题就变成了求解使能量函数 E(D) E ( D ) 最小化的问题.而对于二维平面来说,求解该问题是一个NP完全问题. 如果将图像的每一行独立出来,则该问题转化为一个1D的优化问题,可以使用动态规划进行求解. 但是这样一来就会存在条纹效应(streaking). 因为这样只考虑了水平方向的约束,而对垂直方向的约束很弱甚至没有. 为了解决这个问题,作者在论文中提出了”aggregating matching costs in 1D from all directions equally”, 即对于每一个像素点,计算每一个方向上的一条代价最小路径的和,将之作为聚合后的代价值. 示意图如下:
首先递归定义每个方向上的最小代价:
Lr(p,d)=C(p,d)+min[Lr(p−r,d),Lr(p−r,d−1)+P1,Lr(p−r,d+1)+P1,mini[Lr(p−r,i)+P2]−minkLr(p−r,k)]>(3a) (3a) L r ( p , d ) = C ( p , d ) + min [ L r ( p − r , d ) , L r ( p − r , d − 1 ) + P 1 , L r ( p − r , d + 1 ) + P 1 , min i [ L r ( p − r , i ) + P 2 ] − min k L r ( p − r , k ) ] >
则对于每个像素点,其聚合代价定义如下:
S(p,d)=∑rLr(p,d)>(3b) (3b) S ( p , d ) = ∑ r L r ( p , d ) > (4) 视差计算(Disparity Computation)
由(3)最小化聚合代价, 我们可以得到视差图 D=mindS[p,d] D = min d S [ p , d ] , 分别对左右两张图都进行上述计算,则有:
Dbp=mindS(bp,d)>(4a) (4a) D b p = min d S ( b p , d ) >
Dmp=mindS(np,d)>(4b) (4b) D m p = min d S ( n p , d ) >然后进行视差一致性检验(disparity consistency check), 得到最终的视差图 Dp D p :
Dp={DbpDinvalidif |Dbp−Dmq|≤disp12MaxDiffothers>(4c) (4c) D p = { D b p i f | D b p − D m q | ≤ d i s p 12 M a x D i f f D i n v a l i d o t h e r s >
q=ebm(p,Dbp)>(4d) (4d) q = e b m ( p , D b p ) > (5) Disparity Refinement
(i) Removal of Peaks: 对上一步得到的视差图,利用区域生长的, 取得不同的区域
Ci=∑p(|Dp−Di|≤speckleRange)>(5.1a) (5.1a) C i = ∑ p ( | D p − D i | ≤ s p e c k l e R a n g e ) >
对得到的所有区域, 统计该区域的像素点的个数, 将之作为该区域的大小 Size(Ci)=COUNT(Ci) S i z e ( C i ) = C O U N T ( C i ) , 如果区域大小小于某一阈值,则认为该区域为speckle, 将区域内视差值都标记为非法值:
Dp={DpDinvalidif Size(Ci)<speckleWindowSizeothers> D p = { D p i f S i z e ( C i ) < s p e c k l e W i n d o w S i z e D i n v a l i d o t h e r s >
(5) Birchfield-Tomasi 代价函数根据块聚集代价图计算视差图

I−R=IR^(xR−12)=12(IR(xR)+IR(xR−1))>(4a) (4a) I R − = I R ^ ( x R − 1 2 ) = 1 2 ( I R ( x R ) + I R ( x R − 1 ) ) >
I+R=IR^(xR+12)=12(IR(xR)+IR(xR+1))>(4b) (4b) I R + = I R ^ ( x R + 1 2 ) = 1 2 ( I R ( x R ) + I R ( x R + 1 ) ) >
Imin=min(I−R,I+R,IR(xr))>(4c) (4c) I m i n = min ( I R − , I R + , I R ( x r ) ) >
Imax=max(I−R,I+R,IR(xr))>(4d) (4d) I m a x = max ( I R − , I R + , I R ( x r ) ) >
d¯(xL,xR,IL,IR)=max(0,IL(xL)−Imax,Imin−IL(xL))>(4e) (4e) d ¯ ( x L , x R , I L , I R ) = max ( 0 , I L ( x L ) − I m a x , I m i n − I L ( x L ) ) >对于另外一张图,具有类似的对称定义 d¯(xR,xL,IL,IR) d ¯ ( x R , x L , I L , I R ) .
3. 算法流程
4. 注意事项
OpenCV中的SGBM算法与原始论文中的算法略有不同,主要体现在以下几个点(SGBM API文档):
(1) 算法中计算聚合代价(aggregation cost)时, 计算的是8个方向上的聚合代价,而实现中默认只计算5个方向, 可以通过在创建SGBM对象时通过设置mode = StereoSGBM::MODE_HH 来改变算法行为, 使之计算8个方向.
(2) 原始论文中使用的是单像素匹配, 实现使用的是块匹配(block match). 可以通过设置blockSize = 1 来将块匹配降级为单像素匹配.
(3) 原始论文使用互信息(mutual information)作为匹配的代价函数, 实现中使用一种更简单的, 在参考资料[2]中提出的Birchfield-Tomasi 代价函数.
(4) 实现了参考资料[3] 中使用的一些后处理方法, 提高算法结果.
重要API参数解析
1. StereoBinaryBM
(1) StereoBinaryBM::create()
/**
@brief Creates StereoBM object
@param numDisparities 视差值d的搜索范围.
@param blockSize 进行块聚合代价计算时的块窗口大小.必须为奇数!
*/
static Ptr create(
int numDisparities = 0,
int blockSize = 9); 2. StereoBinarySGBM
(1) StereoBinarySGBM::create()64
/**
@brief Creates StereoSGBM object
@param minDisparity 视差值的最小值.
@param numDisparities Maximum disparity minus minimum disparity.
@param blockSize 块匹配的窗口大小, 必须为奇数且应在[3,11]区间内取值.
@param P1 公式(3a)中的P1. The first parameter controlling the disparity smoothness.
This parameter is used for the case of slanted surfaces (not fronto parallel).
@param P2 公式(3a)中的P2. The second parameter controlling the disparity smoothness.
This parameter is used for "solving" the depth discontinuities problem. The
larger the values are, the smoother the disparity is.
P1 is the penalty on the disparity change by plus or minus 1 between neighbor
pixels. P2 is the penalty on the disparity change by more than 1 between
neighbor
@param disp12MaxDiff 在对视差值进行左右交叉验证时,允许对应像素点处出现的左右视差的最大差值.
prefiltered image pixels. The algorithm first computes x-derivative at each
pixel and clips its Birchfield-Tomasi pixel cost function.
@param uniquenessRatio Margin in percentage by which the best (minimum) computed
cost function value should "win" the second best value to consider the found
match correct. Normally, a value within the 5-15 range is good enough.
对算法在边缘处的视差值具有较大影响,使用默认值即可.
@param speckleWindowSize Maximum size of smooth disparity regions to consider
their noise speckles and invalidate. Set it to 0 to disable speckle filtering.
Otherwise, set it somewhere in the 50-200 range.
@param speckleRange 计算区域大小时,判断两个点是否属于同一区域的差值阈值. Maximum disparity
variation within each connected component. If you do speckle filtering, set
the parameter to a positive value, it will be implicitly multiplied by 16.
Normally, 1 or 2 is good enough.
@param mode Set it to StereoSGBM::MODE_HH to run the full-scale two-pass dynamic
programming algorithm. It will consume O(W\*H\*numDisparities) bytes, which
is large for 640x480 stereo and huge for HD-size pictures.
By default, it is set to false .
*/
static Ptr create(
int minDisparity,
int numDisparities,
int blockSize,
int P1 = 100,
int P2 = 1000,
int disp12MaxDiff = 1,
int preFilterCap = 0,
int uniquenessRatio = 5,
int speckleWindowSize = 400,
int speckleRange = 200,
int mode = StereoBinarySGBM::MODE_SGBM); 一些使用该模块时的注意事项
- numDisparities 参数对于算法性能影响很大, 应尽量设得小一些, 单应能被16整除.
- blockSize 参数一般应设在[3, 11]内, 根据不同的CT变换核函数, 其范围略微有所不同.
运行效果截图
Input Image size: [384 x 288]
BM Costs: 47.3848 ms
SGBM Costs: 35.6961 ms
numDisparities: 64
blockSize: 9输入左右视图:
左视图
右视图
真实视差图:
BM算法得到的视差图(归一化到0-255):
SGBM算法得到的视差图(归一化到0-255):