时间序列分析预测实战之ARIMA模型
接着上一章的内容,当数据超过100个,要对数据进行更加精准的预测,该用什么样的方法呢?
这时候ARIMA模型就登场了,全称是自回归差分移动平均模型,使用这个模型建模,具体的操作步骤如下:
1)观察时序的平稳性和随机性;
2)选择具体的模型;
3)拟合模型;
4)根据选定模型进行预测;
5)模型评价;
我将用一个实际的例子分步骤进行详细的讲解。
一、观察时序的平稳性和随机性
这里选择用R语言进行建模,R语言中ARIMA模型在forecast包中,同时还需要下载zoo包
> install.packages("zoo")
> install.packages("forecast") #下载forecast包时,其实同步下载包括xts,tseries等等包
> library(zoo) #注意必须先加载zoo,再加载forecast包
> library(forecast)这里我选择使用forecast包中自带的wineind数据集来展开实例讲解,共有176个月数据,从1980年1月到1994年8月澳大利亚的全国总销售酒量
> str(wineind) #了解下数据的基本情况,包含值个数
Time-Series [1:176] from 1980 to 1995: 15136 16733 20016 17708 18019 ...
> head(wineind,10)
Jan Feb Mar Apr May Jun Jul Aug Sep Oct
1980 15136 16733 20016 17708 18019 19227 22893 23739 21133 22591
> summary(wineind)
Min. 1st Qu. Median Mean 3rd Qu. Max.
13652 22115 24669 25392 28461 40226 首先绘制历年酒销量的时序图:
观察时序图,可以发现数据具有周期性、长期增长的趋势,并非在某一个常数上下波动,因此主观判断该序列为非平稳时间序列。使用tseries包中的adf.test()函数进行单位根检验,原假设是序列非平稳,备择假设是序列平稳,但检测出来的结果显示P值为0.01<0.05,拒绝原假设,认为该序列平稳,实际上已经知道数据有长期趋势,应该还是当做非平稳数据进行差分处理,并且使用unitrootTest()和adftest()的结果均是P>0.05接受原假设,认为数据非平稳,所以实际中应该多尝试用几个方法得出最终结论。
> adf.test(wineind,k=0)
Augmented Dickey-Fuller Test
data: wineind
Dickey-Fuller = -11.325, Lag order = 0, p-value = 0.01
alternative hypothesis: stationary
> unitrootTest(wineind) #来自fUnitRoots包,默认数据滞后一期
Title:
Augmented Dickey-Fuller Test
Test Results:
PARAMETER:
Lag Order: 1
STATISTIC:
DF: -1.169
P VALUE:
t: 0.2208
n: 0.4428
> adfTest(wineind) #默认数据滞后一期
Title:
Augmented Dickey-Fuller Test
Test Results:
PARAMETER:
Lag Order: 1
STATISTIC:
Dickey-Fuller: -1.169
P VALUE: 0.2421 对非平稳序列进行差分处理,变成平稳序列,这里使用ndiffs()函数判断差分次数
> ndiffs(wineind)
[1] 1函数给出结果为一阶差分,对数据进行一阶差分操作,观察差分后的数据的自相关图和偏自相关图:
> winediff<-diff(wineind)
> plot.ts(winediff,main="一阶差分后的时序图")
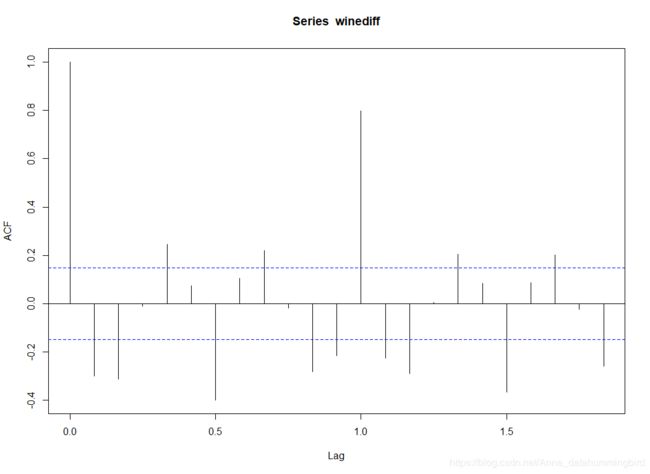
> acf(winediff) #绘制自相关图
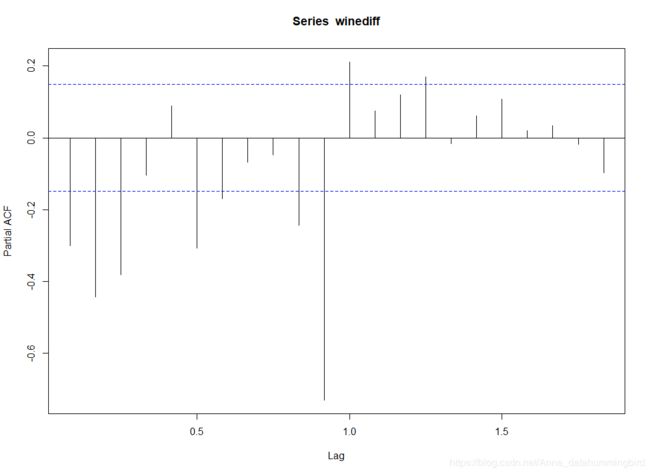
> pacf(winediff) #绘制偏自相关图一阶差分后的时序图没有明显的线性趋势了,处理还是比较成功,但仍能看到周期为12的周期性,接下来如何去观察自相关图和偏自相关图是个技术活,需要理解两个概念拖尾和截尾:
拖尾:相关系数单调递减至0
截尾:相关系数在某个位置突然变成0 (两条蓝色虚线之间可以视作0)
二、模型选择
阶数与模型的选择间的关系详见下图:
| 自相关图(ACF) | 偏自相关图(PACF) | 模型 |
| 拖尾 | P阶截尾 | AR(p) |
| q阶截尾 | 拖尾 | MA(q) |
| q阶拖尾 | P阶拖尾 | ARIMA(p,d,q) |
| 存在明显周期性,且在首次差分后仍然存在明显周期性,P,D,Q指二次差分后图形对应观测参数,m指二次差分次数 | ARIMA(p,d,q)(P,D,Q)[m] | |
对上面的acf图和pacf图进行观察,得到阶数,主要看偏自相关图实际是逐步在减少,可以认为是拖尾,自相关图有两个系数明显异常可以认为是2阶截尾,那么这里就是初步得出是 ARIMA(0,1,2),因为数据具有周期性,现在按照周期数再进行差分,
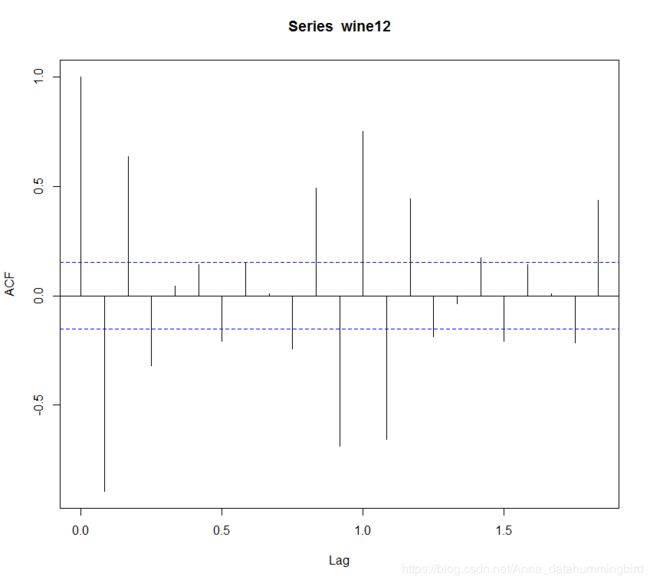
进行12阶差分后,acf图和pacf图如上,偏自相关呈现拖尾,自相关属于不明显的1阶截尾,认为整个模型满足ARIMA(0,1,2)(0,1,1)[12]。
三、模型拟合
> pre<-arima(wineind,order=c(0,1,2),seasonal=list(order=c(0,1,1),period=12),method="ML")
> pre
Call:
arima(x = wineind, order = c(0, 1, 2), seasonal = list(order = c(0, 1, 1), period = 12),
method = "ML")
Coefficients:
ma1 ma2 sma1
-1.0398 0.1474 -0.6532
s.e. 0.0922 0.0918 0.0812
sigma^2 estimated as 5327733: log likelihood = -1497.95, aic = 3003.9拟合ARIMA模型,使用极大似然估计,最后得到模型的AIC值为3003.9,AIC值是判断模型拟合好坏的标准,越小越好。
forecast中的auto.arima()可以直接筛选出最佳拟合模型,一起来看看拟合结果:
> auto.arima(wineind,trace=T)
Fitting models using approximations to speed things up...
ARIMA(2,1,2)(1,1,1)[12] : 2794.566
ARIMA(0,1,0)(0,1,0)[12] : 2918.738
ARIMA(1,1,0)(1,1,0)[12] : 2880.387
ARIMA(0,1,1)(0,1,1)[12] : 2789.402
ARIMA(0,1,1)(1,1,1)[12] : 2797.908
ARIMA(0,1,1)(0,1,0)[12] : 2827.788
ARIMA(0,1,1)(0,1,2)[12] : 2788.526
ARIMA(1,1,1)(0,1,2)[12] : 2788.043
ARIMA(1,1,0)(0,1,2)[12] : 2851.21
ARIMA(1,1,2)(0,1,2)[12] : Inf
ARIMA(0,1,0)(0,1,2)[12] : 2885.681
ARIMA(2,1,2)(0,1,2)[12] : Inf
ARIMA(1,1,1)(1,1,2)[12] : 2797.239
ARIMA(1,1,1)(0,1,1)[12] : 2787.4
ARIMA(2,1,1)(0,1,1)[12] : 2789.621
ARIMA(1,1,0)(0,1,1)[12] : 2853.877
ARIMA(1,1,2)(0,1,1)[12] : 2787.155
ARIMA(2,1,3)(0,1,1)[12] : Inf
ARIMA(1,1,2)(1,1,1)[12] : 2799.39
ARIMA(1,1,2)(0,1,0)[12] : Inf
ARIMA(1,1,2)(1,1,2)[12] : 2798.977
ARIMA(0,1,2)(0,1,1)[12] : 2789.574
ARIMA(2,1,2)(0,1,1)[12] : Inf
ARIMA(1,1,3)(0,1,1)[12] : Inf
Now re-fitting the best model(s) without approximations...
ARIMA(1,1,2)(0,1,1)[12] : 3004.485
Best model: ARIMA(1,1,2)(0,1,1)[12]
Series: wineind
ARIMA(1,1,2)(0,1,1)[12]
Coefficients:
ar1 ma1 ma2 sma1
0.4299 -1.4673 0.5339 -0.6600
s.e. 0.2984 0.2658 0.2340 0.0799
sigma^2 estimated as 5399312: log likelihood=-1497.05
AIC=3004.1 AICc=3004.48 BIC=3019.57系统自动进行计算、筛选,最终选出的最佳模型是: ARIMA(1,1,2)(0,1,1)[12],对应AIC值为3004.1,注意!这里的最佳模型并不如我们自助拟合的ARIMA(0,1,2)(0,1,1)[12]的效果好!
因此,不是直接图便利就能得出最佳结果,实际操作中一定要耐心多尝试,试出最佳结果。
四、根据选定模型进行预测
预测未来6个月的销售值,设置上下95%的置信区间,得到如下预测值:
> wine<-forecast(pre,h=6,level=c(99.5))
> wine
Point Forecast Lo 99.5 Hi 99.5
Sep 1994 25303.28 18824.106 31782.46
Oct 1994 27217.61 20733.298 33701.92
Nov 1994 31928.30 25406.655 38449.94
Dec 1994 37339.48 30780.720 43898.24
Jan 1995 16023.53 9427.859 22619.20
Feb 1995 21405.69 14773.318 28038.07五、模型评价
1.判断预测误差是否是平均值为零且方差为常数的正态分布;
2.使用box.test()对模型的残差进行独立性检验
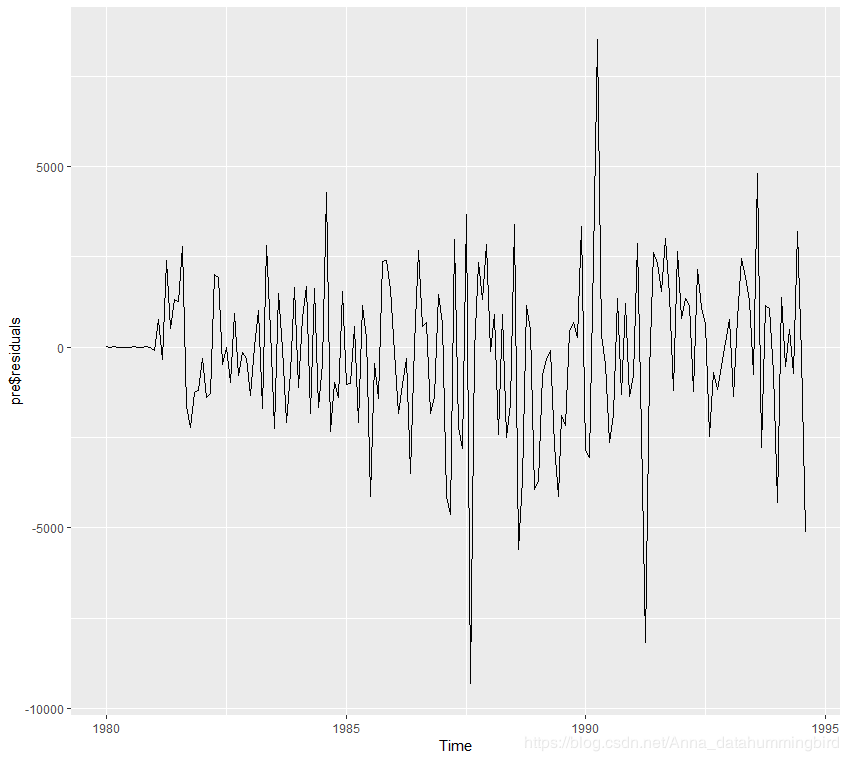
> library(ggplot2)
> autoplot(pre$residuals)残差图如上,要转换成正态分布图,需要构造函数这里参考了https://blog.csdn.net/howardge/article/details/42002733中提供的代码,感谢分享,构造了一个plotForecastErrors()函数:
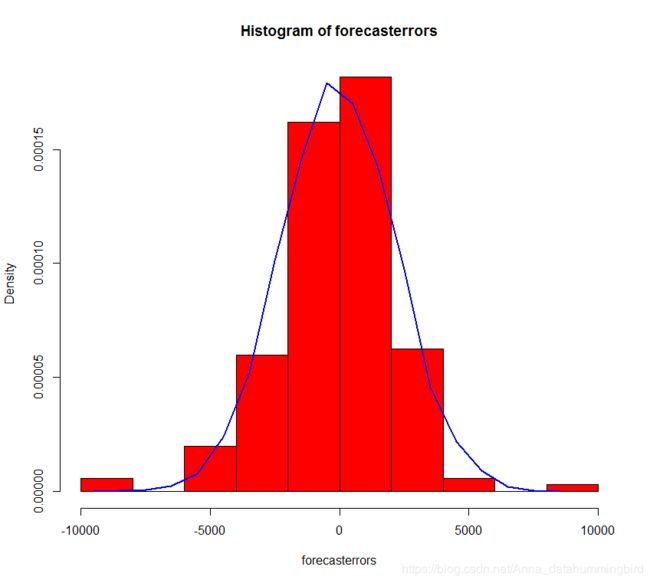
plotForecastErrors <- function(forecasterrors)
{
# make a red histogram of the forecast errors:
mysd <- sd(forecasterrors)
hist(forecasterrors, col="red", freq=FALSE)
# freq=FALSE ensures the area under the histogram = 1
# generate normally distributed data with mean 0 and standard deviation mysd
mynorm <- rnorm(10000, mean=0, sd=mysd)
myhist <- hist(mynorm, plot=FALSE)
# plot the normal curve as a blue line on top of the histogram of forecast errors:
points(myhist$mids, myhist$density, type="l", col="blue", lwd=2)
}
> plotForecastErrors(pre$residuals) 得到如上正态分布图,正态性检验通过,接下来进行残差的独立性检验
> acf(pre$residuals)
> Box.test(pre$residuals, lag=1, type="Ljung-Box")构造残差的自相关图,确定box检验中的lag的系数为1
> Box.test(pre$residuals, lag=1, type="Ljung-Box")
Box-Ljung test
data: pre$residuals
X-squared = 0.019042, df = 1, p-value = 0.8902
P值为0.8902>0.05,拒绝原假设,认为残差是独立的。
因此模型的两个检验均通过,模型拟合效果不错。
> autoplot(wine)最终拟合的图形如上所示,基本符合数据趋势规律,可以进一步结合实际业务进行优化,得出能够经得起实战考验的结果。
ARIMA模型的讲解到此结束,比较复杂需要耐心去钻研下,最好多练习几次才能更好理解和运用,有问题欢迎讨论!