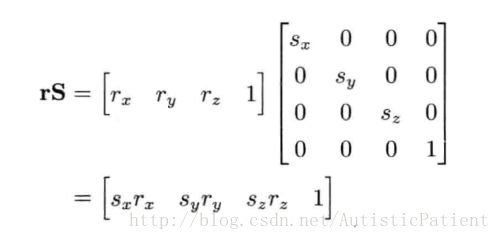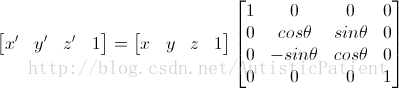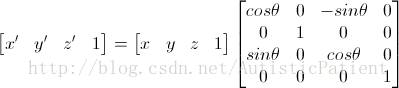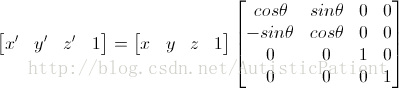3D数学基础之C#实现矩阵变换
Never put off what you can do today until tomorrow.
从刚开始学unity各种组件,C#基础,API,到现在的学习Cg语言,学习shaderLab
用了很长时间在细节上,有的时候一些看似非常基础的概念,大致了解下怎么用后,如果不知道其原理,那么,我认为是不可能真正的学会一种技术的。
本节就来实现矩阵与向量之间的计算,,我们将自己实现向量的类和矩阵的类,这也就代表着,我们必须实现基本的Mul功能
tools:visual studio 2015 建议安装插件:resharper.
step1
首先,关于C#语法,以及内置函数,这里不会解释的,大家可以搜索API或者MSDN
为了不在代码处做过多数学赘述,第一步将会介绍矩阵的几何变换(3种)
矩阵的平移变换Translation
将三维空间中的一个点移动到另一个点,随便Google了一张图 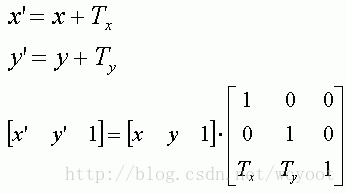
其中平移变换的结果为等号左侧,平移变换的计算在等号右侧,回想下矩阵乘法的运算规则
这里的运算为
X偏移量 = (X x 1 + Y x 0 + 1 x Tx) = X + Tx 也就是在X上的偏移量
同理: Y的偏移量 = (X x 0 + Y x 1 + 1 x Ty) = Y + Ty 也就是在Y上的偏移量
算到这里大家应该明白为什么三维向量和矩阵的运算,要用到Vector4了,因为w = 1方便我们跟矩阵做乘法。
矩阵的缩放变换
将模型放大或者缩小,本质也是对模型上每个顶点进行放大和缩小(顶点坐标值变大或变小)
矩阵的旋转变化
这个是本系列中会用到的,很重要,这里只说绕坐标轴旋转,来源Google图片
绕X轴旋转:顶点的X坐标不变,y坐标和z坐标绕X轴旋转θ度,旋转的正方向为顺时针方向,也就是逆时针是正方向,从图中可以看出,X的旋转结果 = X x 1 + Y x 0 + Z x 0 + 1 x 0 = X 这里可以解释绕X轴旋转X轴的顶点坐标不变
Y的旋转结果:X x 0 + Ycos(a) - Zsin(a) + 0 = Ycos(a) - Zsin(a) Z轴的旋转同理,最后,W = 1.
这是绕X轴旋转的公式
上面的分别是绕Y轴旋转和绕Z轴旋转的公式。
刚才讲了公式,并没有写公式的推导(懒/(ㄒoㄒ)/~~)
Ok,知道了矩阵的几何变换,下面进入实战
step2
接下来进入vs2015 新建c#窗体应用程序
我认为还是有必要提一下,本篇只是对3D数学中矩阵的计算加深理解,并不想重复造轮子
(1)首先要实现矩阵和向量的之间的计算,我们要先实现向量类,在资源管理器处右键新建类
class Vector4
{
public double x, y, z, w;
public Vector4()
{
}
public Vector4(double x,double y,double z,double w)
{
this.x = x;
this.y = y;
this.z = z;
this.w = w;
}
//用来copy外部声明的向量
public Vector4(Vector4 vector4)
{
this.x = vector4.x;
this.y = vector4.y;
this.z = vector4.z;
this.w = vector4.w;
}
}这个向量类没什么解释的,简单的构造函数重载
(2)接下来实现矩阵类,一样右键新建类
//16个元素
class matrix4X4
{
private double[,] ptsDoubles;
//无参构造函数,Initialize
public matrix4X4()
{
ptsDoubles = new double[4, 4];
}
//索引器,帮助我们通过传递索引,便可轻松拿到数组每一个元素
public double this[int i, int j]
{
get { return ptsDoubles[i - 1,j - 1]; }
set { ptsDoubles[i - 1,j - 1] = value; }
}
//实现矩阵的乘法规则,这个没啥难的,大家复习下乘法规则就明白了,不要被三个for吓到
public matrix4X4 MulMatrix4X4(matrix4X4 m)
{
matrix4X4 newMatrix4X4 = new matrix4X4();
for (int w = 0; w <= 4; w++)
for (int h = 0; h <= 4; h++)
for (int n = 0; n <= 4; n++)
{
newMatrix4X4[w, h] += this[w, n] * m[n,h];
}
return newMatrix4X4;
}
//向量与矩阵的乘法运算,返回一个新的向量
public Vector4 MulVector4(Vector4 v)
{
Vector4 newVector4 = new Vector4();
newVector4.x = v.x * this[1, 1] + v.y * this[2, 1] + v.z * this[3, 1] + v.w * this[4, 1];
newVector4.y = v.x * this[1, 2] + v.y * this[2, 2] + v.z * this[3, 2] + v.w * this[4, 2];
newVector4.z = v.x * this[1, 3] + v.y * this[2, 3] + v.z * this[3, 3] + v.w * this[4, 3];
newVector4.w = v.x * this[1, 4] + v.y * this[2, 4] + v.z * this[3, 4] + v.w * this[4, 4];
return newVector4;
}
}实现了4x4矩阵的类,该注释的地方都解释了,不明白的私信吧,这里需要注意的是,在c#里或者unity封装好的矩阵里,应该不会用这么简单的方法来定义矩阵,只是加深理解的作用
(3)接下来实现三角形的3D变换,新建Triangle3D类
class Triangle3D
{
private Vector4 a, b, c;
public Vector4 A, B, C;
public Triangle3D() { }
public Triangle3D(Vector4 a,Vector4 b,Vector4 c)
{
//这里面可以回想一下vector4类里的copy函数,其实就是做一个新的引用
this.A = this.a = new Vector4(a);
this.B = this.b = new Vector4(b);
this.C = this.c = new Vector4(c);
}
//三角形利用矩阵(m)的乘法进行变换,其实变换的就是顶点
public void Transfrom(matrix4X4 m)
{
//这里新声明了私有的向量,对应A,B,C
//如果在原有变量上修改,那么就会改变原有变量的引用空间
this.a = m.MulVector4(this.A);
this.b = m.MulVector4(this.B);
this.c = m.MulVector4(this.C);
}
//绘制三角形到2D窗口,其实放在unity editor里实现会更加easy
public void Draw(Graphics graphics)
{
graphics.TranslateTransform(300,300);
graphics.DrawLines(new Pen(Color.Red,2),this.Get2DPointarr());
}
private PointF[] Get2DPointarr()
{
//想要在2D平面画出三角形,必须首尾连接
PointF[] arr = new PointF[4];
arr[0] = Get2DPointF(this.a);
arr[1] = Get2DPointF(this.b);
arr[2] = Get2DPointF(this.c);
arr[3] = arr[0];
return arr;
}
//在二维平面定义点
private PointF Get2DPointF(Vector4 v)
{
PointF p = new PointF();
p.X = (float)(v.x / v.w);
p.Y = (float)(v.y / v.w);
return p;
}
}//接下来是最后的form窗口
//如果对矩阵计算熟悉些的话,这个Form窗体程序还是很好理解的
//怎么打开这个事件函数 这个 就不截图了吧。。
public partial class Form1 : Form
{
private int a = 0;
private Triangle3D triangle3D;
private matrix4X4 m_Scale; //缩放矩阵
private matrix4X4 m_rotate; //旋转矩阵
private matrix4X4 m_view; //摄像机矩阵
private matrix4X4 m_Projection; //视图矩阵
//这里面所有的矩阵计算都是根据上面的乘法规则
public Form1()
{
InitializeComponent();
m_rotate = new matrix4X4();
m_Scale = new matrix4X4();
m_Scale[1, 1] = 250;
m_Scale[2, 2] = 250;
m_Scale[3, 3] = 250;
m_Scale[4, 4] = 1;
m_view = new matrix4X4();
m_view[1, 1] = 1;
m_view[2, 2] = 1;
m_view[3,3] = 1;
m_view[4, 3] = 250;
m_view[4, 4] = 1;
m_Projection = new matrix4X4();
m_Projection[1, 1] = 1;
m_Projection[2, 2] = 1;
m_Projection[3, 3] = 1;
m_Projection[3,4] = 1.0 / 250;
}
private void Form1_Load(object sender, EventArgs e)
{
//w一定要是1,然后跟矩阵相乘才能进行正常的变换
Vector4 a = new Vector4(0,-0.5,0,1);
Vector4 b = new Vector4(0.5,0.5,0,1);
Vector4 c = new Vector4(-0.5,0.5,0,1);
triangle3D = new Triangle3D(a,b,c);
triangle3D.Transfrom(m_Scale);
}
//然后可以开始绘制窗体事件
private void Form1_Paint(object sender, PaintEventArgs e)
{
triangle3D.Draw(e.Graphics);
}
//这个函数是通过time空间添加进来的,目的是随着时间的推移,顶点也跟着变换
private void timer1_Tick(object sender, EventArgs e)
{
//现在是角度
a += 2;
//计算出弧度
double angle = a / 360.0 * Math.PI;
//矩阵的几何变换
m_rotate[1, 1] = Math.Cos(angle);
m_rotate[1, 3] = Math.Sin(angle);
m_rotate[2, 2] = 1;
m_rotate[3, 1] = -Math.Sin(angle);
m_rotate[3, 3] = Math.Cos(angle);
m_rotate[4, 4] = 1;
matrix4X4 m = m_Scale.MulMatrix4X4(m_rotate);
m = m.MulMatrix4X4(m_view);
m = m.MulMatrix4X4(m_Projection);
triangle3D.Transfrom(m);
//重绘
this.Invalidate();
}
}这样 就可以实现一个三角形在空间视图进行3D旋转
如果看完很蒙 ,可能是我表达的不够仔细,这个程序是我在网上找的,当时对矩阵和向量的计算一点都不了解,看完这个感觉很爽嗒~
如果对整个winform程序不理解不了,那我建议大家可以试着先实现上面的vector4 和 matrix4x4 相信你会有所收获的
最后推荐大家一个vs插件:resharper,以前只支持.net,现在也支持c++了,我之所以在上述程序中没解释的那么详细,就是因为它,它的代码提示功能太强了(中文的提示),当然它的功能还有很多
缺点:太胖啦!!!