概率统计----均值,方差,协方差,相关系数,协方差矩阵
机器视觉中,常用到协方差相关的知识,特别是基于统计框架下的机器学习算法,几乎无处不在的用到它,因此了解协方差是再基础不过的了。这里推荐一个很不错的基础教程:协方差的意义和计算公式
-
均值和方差
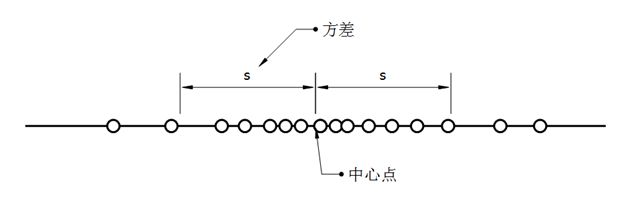
引入协方差之前,先简单回顾下概率统计中的两个重要基础概念:均值和方差。均值,顾名思义就是一堆样本的平均值,方差就是样本和均值的平均偏差。对于给定的n个样本,那么样本集的均值和方差可以分别这样来定义:
| 名称 |
公式 |
解释 |
| 均值 |
X¯=∑ni=1XinX¯=∑i=1nXin |
样本的平均值,即样本的中心点,例如{1 2,3,4}的均值是2.5 |
| 标准差 |
S=∑ni=1(Xi−X¯)2n−1−−−−−−−−−√S=∑i=1n(Xi−X¯)2n−1 |
样本点到中心点的平均距离,所以这里做了平方再开方。注意这里采用了除以n-1,目的是为了用更少的样本就可以趋近于总体的标准差。例如{1 2,3,4}的标准差 |
| 方差 |
S2=∑ni=1(Xi−X¯)2n−1S2=∑i=1n(Xi−X¯)2n−1 |
样本点到中心点的平均距离的平方,用平方是为了方便计算,因为是一一对应的正相关关系,所以意义和标准差一样,免去了开放带来的复杂计算。 |
![]()
均值(中心点)和方差的图示如下所示:
-
协方差和相关系数
方差描述的是一维数据上的统计量。而在实际中,还会考察两个统计量之间的相关性,例如人的身高和两手撑开的长度是否由相关性?男人越坏是不是女人就越爱?那这个时候就可以用协方差来刻画了。
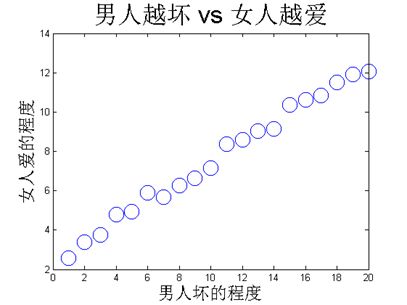
以男人越坏女人越爱为例,假设采访了二十对情侣,得到下面的数据:
| 男人坏的程度 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 女人爱的程度 |
2.58 |
3.39 |
3.75 |
4.80 |
4.93 |
5.91 |
5.68 |
6.26 |
6.64 |
7.13 |
8.36 |
8.57 |
9.04 |
9.14 |
10.35 |
10.62 |
10.85 |
11.51 |
11.90 |
12.07 |
我们画个二维点图,很容易发现,他们是线性相关的,如下图所示:
直观上,如果男人坏的程度和女人爱的程度如果是成正比例的话,就是说如果男人越坏女人越爱男人,那么我们就认为他们是正相关的,如果是反比例的话,就是说男人越坏女人越不爱男人,那么我们就认为他们是负相关的。如果女人爱不爱男人和男人坏不坏没有任何毛关系的话,那么我们就是他们两个变量是毫无关系的,我们也认为他们是独立的,因为互不搭杠嘛。那怎么来描述正相关呢?我们可以这么想,如果两个变量偏离中心点的变化量越一致,那么我们就可以认为他们越正相关的;同样地如果两个变量偏离中心点的变化量刚好相反,那么就是负相关了。根据这个思想我们可以仿照方差来定义协方差:
| 名称 |
公式 |
解释 |
| 方差 |
var(X)=∑ni=1(Xi−X¯)2n−1var(X)=∑i=1n(Xi−X¯)2n−1 |
样本点到中心点的平均距离的平方,用平方是为了方便计算,因为是一一对应的正相关关系,所以意义和标准差一样,免去了开放带来的复杂计算。 |
| 协方差 |
cov(X,Y)=∑ni=1(Xi−X¯)(Yi−Y¯)n−1cov(X,Y)=∑i=1n(Xi−X¯)(Yi−Y¯)n−1 |
两个样本的相关性刻画 |
从定义不难发现,当两个变量正相关性很强的时候,那么其协方差就越大,当两个变量负相关越强,那么其协方差是负数且很小;当两个变量关系不大的时候,那么他们协方差趋于0,越接近独立。根据上面表格的数据,我们计算相应的协方差,其结果为:33.2500,为正,说明是正相关的。需要注意的是,协方差的定义是没有将数据进行归一化的,即两个变量的数据如果尺度不一样,就会导致其中的变量影响大于另外一个变量,例如一个变量的取值范围为0.1-1,另一个变量取值范围为100-1000,这样后者在计算中起到决定作用,而前者影响则微乎其微,导致协方差不能反应相关性的强弱程度。下面的这段代码解释了这种情况:
![]()
value = [];
for w = 0:5:50
x = 1:50;
y = roundn(0.1*x+2+w*rand(1,size(x,2)),-2);
plot(x,y,'bo');
value = [value sum((x(1,:)-mean(x(1,:))).*(y(1,:)-mean(y(1,:))))/(size(x,2))];
value = roundn(value,-2);
end
![]()
结果为:
随着噪声的增加,协方差并不能刻画相关性的强弱。其实是因为数据没有归一化而导致的结果,这就引入了相关系数的定义,如下:
coef(X,Y)=∑ni=1(Xi−X¯)(Yi−Y¯)n−1∑ni=1(Xi−X¯)2n−1√∑ni=1(Yi−Y¯)2n−1√coef(X,Y)=∑i=1n(Xi−X¯)(Yi−Y¯)n−1∑i=1n(Xi−X¯)2n−1∑i=1n(Yi−Y¯)2n−1
coef(X,Y)=∑ni=1(Xi−X¯)(Yi−Y¯)∑ni=1(Xi−X¯)2√∑ni=1(Yi−Y¯)2√coef(X,Y)=∑i=1n(Xi−X¯)(Yi−Y¯)∑i=1n(Xi−X¯)2∑i=1n(Yi−Y¯)2
再来看下上面的例子用相关系数得到的结果
代码如下:
![]()
value = []; coef = []; for w = 0:5:50 x = 1:50; y = x+w*rand(1,size(x,2)); plot(x,y,'bo'); coef = [coef sum((x(1,:)-mean(x(1,:))).*(y(1,:)-mean(y(1,:))))/(std(x)*std(y)*(size(x,2)))]; coef = roundn(coef,-2); end
![]()
结果为:
由此可见随着噪声的增加,相关性会降低,而相关系数的值也会趋于0.相关性越强,则相关系数的值会越大。
从定义可知,协方差和相关系数具有交换性,即
cov(X,Y)=cov(Y,X)cov(X,Y)=cov(Y,X)
coef(X,Y)=coef(Y,X)coef(X,Y)=coef(Y,X)
当两个变量相同时,协方差等于方差,即
cov(X,Y)=s2,ifX=Ycov(X,Y)=s2,ifX=Y
实际上,如果数据归一化后,得到的协方差,是具有相关系数相同的性质,也可以用来刻画相关性的强弱。
3、协方差矩阵
当一个样本含有很多变量的时候,如何刻画两两样本之间的相关性呢?需要使用协方差矩阵来表示,就是用一个矩阵把两两变量之间的协方差存储起来而已,由于协方差具有交换性,只需
要计算上三角或下三角的协方差即可,计算量为n!(n−2)!∗2n!(n−2)!∗2 ,协方差矩阵定义如下:
C=⎡⎣⎢⎢c11⋮cn1⋯⋱⋯c1n⋮cnn⎤⎦⎥⎥C=[c11⋯c1n⋮⋱⋮cn1⋯cnn]
其中ci,j=cov(Xi,Yj)ci,j=cov(Xi,Yj)。显而易见地协方差矩阵是一个对角矩阵 ,因此是一个正定矩阵,通常也可逆;对角线上的元素是各个维度上方差。
因此:协方差矩阵是维度之间的协方差构成的矩阵,而不是样本个数构成的,因此拿到样本时,需要搞清楚维度是行还是列。
关于协方差矩阵的示例和意义,请参考资料:协方差矩阵的实例与意义
4、参考文献
- 协方差的意义和计算公式
- 协方差矩阵的实例与意义