数据结构基础26:图
前言:线性表和树两类数据结构,线性表中的元素是“一对一”的关系,树中的元素是“一对多”的关系。而图是一种比线性表和树更复杂的数据结构,在图中,结点之间的关系是任意的,任意两个数据元素之间都可能相关,图是一种“多对多”的数据结构。在计算机科学中,图是最灵活的数据结构之一,很多问题都可以使用图模型进行建模求解。例如:生态环境中不同物种的相互竞争、人与人之间的社交与关系网络、化学上用图区分结构不同但分子式相同的同分异构体、分析计算机网络的拓扑结构确定两台计算机是否可以通信、找到两个城市之间的最短路径等等。
一、图的基本概念
1、图的定义
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
线性表中可以没有元素,称为空表。树中可以没有结点,叫做空树。但是在图中不允许没有顶点,可以没有边。
2、图的种类
①了解图的种类前先了解两个概念:
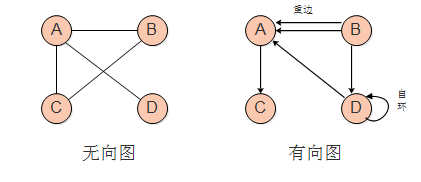
无向边:若顶点Vi和Vj之间的边没有方向,称这条边为无向边(Edge),用(Vi,Vj)来表示。
有向边:若从顶点Vi到Vj的边有方向,称这条边为有向边,也称为弧(Arc),用
②那么我们来看一下图的分类:
-
无向图(Undirected graphs):图中任意两个顶点的边都是无向边。
-
有向图(Directed graphs):图中任意两个顶点的边都是有向边。
-
简单图:不存在自环(顶点到其自身的边)和重边(完全相同的边)的图
-
无环图:没有环的图,其中,有向无环图有特殊的名称,叫做DAG(Directed Acyline Graph)(最好记住,DAG具有一些很好性质,比如很多动态规划的问题都可以转化成DAG中的最长路径、最短路径或者路径计数的问题)。
-
无向完全图:无向图中,任意两个顶点之间都存在边。
-
有向完全图:有向图中,任意两个顶点之间都存在方向相反的两条弧。
-
稀疏图;有很少条边或弧的图称为稀疏图,反之称为稠密图。
-
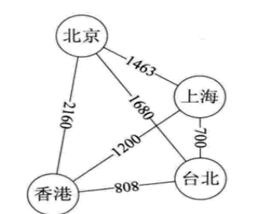
权(Weight):表示从图中一个顶点到另一个顶点的距离或耗费。
-
网:带有权重的图
3、边和顶点的两个重要关系
- 邻接(adjacency):邻接是两个顶点之间的一种关系。如果图包含边(u,v),则称顶点u与顶点v邻接。当然,在无向图中,这也意味着顶点与顶点邻接。
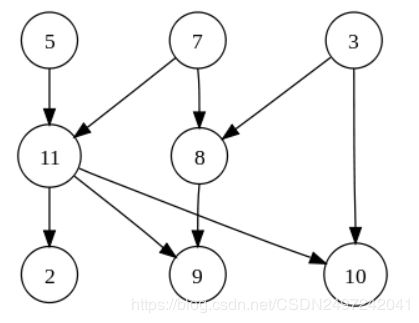
- 关联(incidence):关联是边和顶点之间的关系。在有向图中,边(u,v)从顶点u开始关联到v,或者相反,从v关联到u。注意,有向图中,边不一定是对称的,有去无回是完全有可能的。细化这个概念,就有了顶点的入度(in-degree)和出度(out-degree)。无向图中,顶点的度就是与顶点相关联的边的数目,没有入度和出度。在有向图中,我们以下图为例,顶点10有2个入度,但是没有从10指向其它顶点的边,因此顶点10的出度为0。
4、图的基本术语
-
度:与特定顶点相连接的边数;
-
出度、入度:有向图中的概念,出度表示以此顶点为起点的边的数目,入度表示以此顶点为终点的边的数目;
-
路径(path):依次遍历顶点序列之间的边所形成的轨迹。注意,依次就意味着有序,先1后2和先2后1不一样;
-
简单路径:没有重复顶点的路径称为简单路径。说白了,这一趟路里没有出现绕了一圈回到同一点的情况,也就是没有环;
-
环:第一个顶点和最后一个顶点相同的路径;
-
简单环:除去第一个顶点和最后一个顶点后没有重复顶点的环;
-
连通的:无向图中每一对不同的顶点之间都有路径。如果这个条件在有向图里也成立,那么就是强连通的;
-
连通图:任意两个顶点都相互连通的图;
-
极大连通子图:包含竟可能多的顶点(必须是连通的),即找不到另外一个顶点,使得此顶点能够连接到此极大连通子图的任意一个顶点;
-
连通分量:极大连通子图的数量;
-
强连通图:此为有向图的概念,表示任意两个顶点a,b,使得a能够连接到b,b也能连接到a 的图;
-
生成树:
-
最小生成树:此生成树的边的权重之和是所有生成树中最小的;
-
AOV网(Activity On Vertex Network ):在有向图中若以顶点表示活动,有向边表示活动之间的先后关系
-
AOE网(Activity On Edge Network):在带权有向图中若以顶点表示事件,有向边表示活动,边上的权值表示该活动持续的时间
总结:树可以说只是图的特例,其实树就是有n个顶点,n-1条边,并且保证n个顶点相互连通(不存在环)的图。
二、图的存储结构
图的结构比价复杂,任意两个顶点之间都可能存在关系,不能用简单的顺序存储结构来表示。如果运用多重链表,即一个数据域多个指针域组成的结点表示图中一个结点,则造成大量存储单元浪费或操作不便。
图的三种表示方法:
1、邻接矩阵(Adjacency Matrix)
存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称邻接矩阵)存储图中的边或弧的信息。
①无向图的邻接矩阵:
无向图由于边不区分方向,所以其邻接矩阵是一个对称矩阵。主对角线全为0表示图中不存在自环。其中B的度为2
特点:
a、0表示无边,1表示有边
b、顶点的度是行内数组之和
c、求取顶点邻接点,将行内元素遍历下
②有向图的邻接矩阵:
有向图中讲究入度和出度,各行之和是出度,各列之和是入度。
③带权有向图的邻接矩阵:
在带权有向图的邻接矩阵中,数字表示权值weight,「无穷」表示弧不存在。由于权值可能为0,所以不能像在无向图的邻接矩阵中那样使用0来表示弧不存在。
④邻接矩阵优缺点:
-
优点:结构简单,操作方便
-
缺点:对于稀疏图,这种实现方式将浪费大量的空间。
2、邻接表
一个顶点i的邻接表是一个线性表,它包含所有邻接于顶点i的顶点。邻接表分为邻接链表和邻接数组。在一个图的邻接表描述中,图的每一个顶点都有一个邻接表。
1)邻接链表
邻接链表是将数组与链表相结合的存储方法。
-
图中顶点用一个一维数组存储。
-
图中每个顶点Vi的所有邻接点构成一个线性链表。
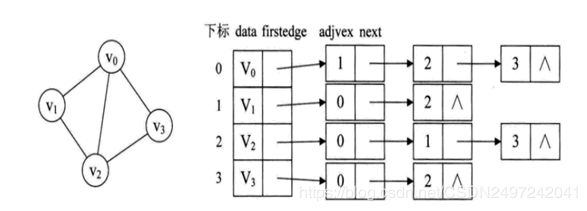
①无向图的邻接链表:
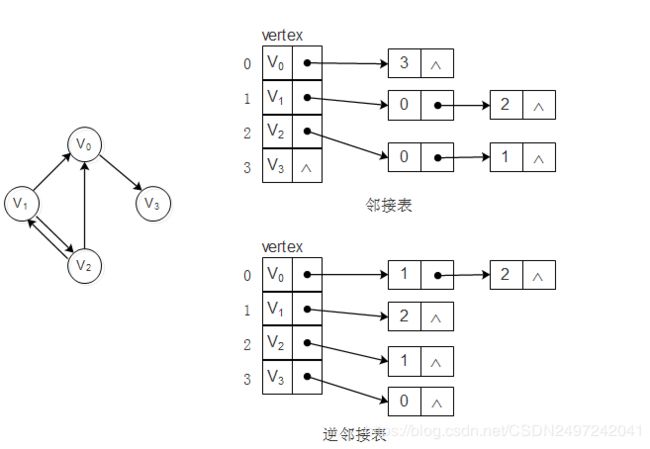
从图中得知,顶点表的各个结点由data和Firstedge两个域表示,data是数据域,存储顶点信息,firstedge是指针域,指向边表的第一个结点,即顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域,存储某顶点的邻接点在顶点表中坐标,next存储边表中下一个结点指针。比如v1顶点与v2、v0互为邻接点,则在v1边表中,adjvex分别为0和2。
②有向图的邻接链表
出度表叫邻接表,入度表叫尾逆邻接表:
有向图的邻接链表是以顶点为弧尾来存储边表的,这样很容易求一个顶点的出度(顶点对应单链表的长度),但若求一个顶点的入度,则需遍历整个图才行。这时可以建立一个有向图的逆邻接表即对每个顶点v都建立一个弧头尾v的单链表。如上图所示
实践中常用邻接链表,其Java代码实现:
/**
* 有向带权图的邻接链表实现
*
*/
public class Graph
{
Map vertexsMap; //存储所有的顶点
int verNums;//顶点数
int edgNums;//边数
private class Vertex{
public String name; //顶点名称
public Edge next; //下一段弧
Vertex(String name, Edge next){
this.name = name;
this.next = next;
}
}
private class Edge{
public String name; //被指向顶点名称
public int weight; //弧的权值
public Edge next; //下一段弧
Edge(String name, int weight, Edge next){
this.name = name;
this.weight = weight;
this.next = next;
}
}
Graph(){
this.vertexsMap = new HashMap<>();
}
//添加顶点
public void insertVertex(String vertexName)
{
Vertex vertex = new Vertex(vertexName, null);
vertexsMap.put(vertexName, vertex);
verNums++;
}
//添加弧
public void insertEdge(String begin, String end, int weight)
{
Vertex beginVertex = vertexsMap.get(begin);
if(beginVertex == null)
{
beginVertex = new Vertex(begin, null);
vertexsMap.put(begin, beginVertex);
}
Edge edge = new Edge(end, weight, null);
if(beginVertex.next == null)
{
beginVertex.next = edge;
}
else
{
Edge lastEdge = beginVertex.next;
while(lastEdge.next != null)
{
lastEdge = lastEdge.next;
}
lastEdge.next = edge;
}
edgNums++;
}
//打印图
public void print()
{
Set> set = vertexsMap.entrySet();
Iterator> iterator = set.iterator();
while(iterator.hasNext()){
Map.Entry entry = iterator.next();
Vertex vertex = entry.getValue();
Edge edge = vertex.next;
while(edge != null){
System.out.println(vertex.name + " 指向 " + edge.name + " 权值为:" + edge.weight);
edge = edge.next;
}
}
}
public static void main(String[] args) {
Graph graph = new Graph();
graph.insertVertex("A");
graph.insertVertex("B");
graph.insertVertex("C");
graph.insertVertex("D");
graph.insertVertex("E");
graph.insertVertex("F");
graph.insertEdge("C", "A", 1);
graph.insertEdge("F", "C", 2);
graph.insertEdge("A", "B", 4);
graph.insertEdge("E", "B", 2);
graph.insertEdge("A", "D", 5);
graph.insertEdge("D", "F", 4);
graph.insertEdge("D", "E", 3);
graph.print();
}
} 2)邻接数组
在邻接数组中,每一个邻接表用一个数组线性表而不是链表来描述。
邻接数组比邻接链表少用4m字节,因为不需要指针域(这样的指针域有m个),对大部分图操作。邻接数组的用时要少于邻接链表。
3、十字链表
在邻接表中针对有向图,分为邻接表和逆邻接表,导致无法从一个表中获取图的入读和出度的情况,有人提出了十字链表。
十字链表(Orthogonal List):是将邻接链表和逆邻接表相结合的存储方法,它解决了邻接表(或逆邻接表)的缺陷,即求入度(或出度)时必须遍历整个图。
其实还有一种表示方式是邻接多重表,有兴趣可以了解一下。
三、图的遍历:BFS和DFS算法
从图的某个顶点出发,遍历图中其余顶点,且使每个顶点仅被访问一次,这个过程叫做图的遍历(Traversing Graph)。对于图的遍历通常有两种方法:深度优先遍历(DFS)和广度优先遍历(BFS)。
DFS和BFS是很多图算法的基础。不过,要获得效率更高的图的算法,深度优先算法使用较多。
3.1、深度优先遍历
深度优先遍历(Depth First Search,简称DFS),也被称为深度优先搜索。这种搜索方法可以用栈来实现,类似老鼠走迷宫。
遍历思想:首先从图中某个顶点v0出发,访问此顶点,然后依次从v相邻的顶点出发深度优先遍历,直至图中所有与v路径相通的顶点都被访问了;若此时尚有顶点未被访问,则从中选一个顶点作为起始点,重复上述过程,直到所有的顶点都被访问。
但其实,深度优先遍历用递归实现会比较简单,只需用一个递归方法来遍历所有顶点,在访问某一个顶点时:
-
将它标为已访问
-
递归的访问它的所有未被标记过的邻接点
/*
* DFS,深度优先搜索算法
*/
public class DFSTraverse
{
private boolean[] visited;
//从顶点index开始遍历
public DFSTraverse(Digraph graph, int index) {
visited = new boolean[graph.getVertexsNum()];
dfs(graph,index);
}
private void dfs(Digraph graph, int index) {
visited[index] = true;
for(int i : graph.adj(index)) {
if(!visited[i])
dfs(graph,i);
}
}
}3.2、广度优先遍历
广度优先遍历(Breadth First Search,简称BFS),又称为广度优先搜索。这种搜索方法可以用队列实现。
遍历思想:首先,从图的某个顶点v0出发,访问了v0之后,依次访问与v0相邻的未被访问的顶点,然后分别从这些顶点出发,广度优先遍历,直至所有的顶点都被访问完。
/*
* BFS,广度优先搜索
*/
public class BFSTraverse {
private boolean[] visited;
public BFSTraverse(AdjListDigraph graph, int index) {
visited = new boolean[graph.getVertexsNum()];
bfs(graph,index);
}
private void bfs(AdjListDigraph graph, int index) {
//在JSE中LinkedList实现了Queue接口
Queue queue = new LinkedList<>();
visited[index] = true;
queue.add(index);
while(!queue.isEmpty()) {
int vertex = queue.poll();
for(int i : graph.adj(vertex)) {
if(!visited[i]) {
visited[i] = true;
queue.offer(i);
}
}
}
}
} 四、最小生成树算法
4.1、最小生成树概念
图的生成树是它的一棵含有所有顶点的无环连通子图。一棵加权图的最小生成树(MST)是它的一棵权值(所有边的权值之和)最小的生成树。
最小生成树的定义:
(1)一个带权值的图:网。所谓最小成本,就是用n-1条边把n个顶点连接起来,且连接起来的权值最小。
(2)我们把构造联通网的最小代价生成树称为最小生成树
(3)普里姆算法和克鲁斯卡尔算法
4.2、计算最小生成树可能遇到的情况
-
非连通的无向图,不存在最小生成树
-
权重不一定和距离成正比
-
权重可能是0或负数
-
若存在相等的权重,那么最小生成树可能不唯一
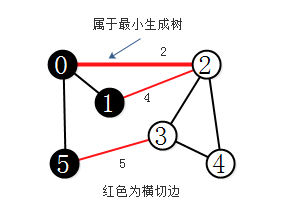
图的切分是将图的所有顶点分为两个非空且不重叠的两个集合。横切边是一条连接两个属于不同集合的顶点的边。
切分定理:在一幅加权图中,给定任意的切分,它的横切边中的权重最小者必然属于图的最小生成树。
切分定理是解决最小生成树问题的所有算法的基础。这些算法都是贪心算法。
首先实现一个带权的无向图,Java代码:
//定义边
public class Edge implements Comparable{
private final int ver1;
private final int ver2;
private final Integer weight;
public Edge(int ver1, int ver2, int weight) {
super();
this.ver1 = ver1;
this.ver2 = ver2;
this.weight = weight;
}
//返回一个顶点
public int either() {
return ver1;
}
//返回另一个顶点
public int other(int vertex) {
if (vertex == ver1)
return ver2;
else if(vertex == ver2)
return ver1;
else
throw new RuntimeException("边不一致");
}
@Override
public int compareTo(Edge e) {
return this.weight.compareTo(e.weight);
}
public Integer getWeight() {
return weight;
}
@Override
public String toString() {
return "Edge [" + ver1 + "," + ver2 +"]";
}
}
/**
* 带权无向图的实现
*/
public class WeightedGraph {
private final int vertexsNum;
private final int edgesNum;
private List[] adj;
public WeightedGraph(int[][] data, int vertexsNum) {
this.vertexsNum = vertexsNum;
this.edgesNum = data.length;
adj = (List[]) new ArrayList[vertexsNum];
for(int i=0; i();
}
for (int i = 0; i < data.length; i++) {
Edge edge = new Edge(data[i][0],data[i][1],data[i][2]);
int v = edge.either();
adj[v].add(edge);
adj[edge.other(v)].add(edge);
}
}
public Iterable adj(int vertex) {
return adj[vertex];
}
public int getVertexsNum() {
return vertexsNum;
}
public int getEdgesNum() {
return edgesNum;
}
public Iterable getEdges() {
List edges = new ArrayList<>();
for(int i=0; i e.other(i)) { //无向图,防止将一条边加入两次
edges.add(e);
}
}
}
return edges;
}
} 4.3、应用场景
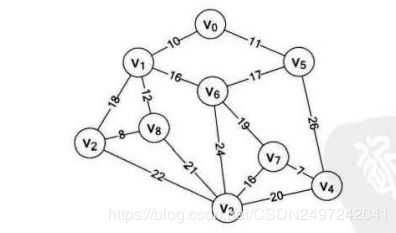
设想有9个村庄,这些村庄构成如下图所示的地理位置,每个村庄的直线距离都不一样。若要在每个村庄间架设网络线缆,若要保证成本最小,则需要选择一条能够联通9个村庄,且长度最小的路线。
4.4、有两种实现算法:Prim算法和Kruskal算法
五、单源最短路径算法
最短路径指两顶点之间经过的边上权值之和最少的路径,并且称路径上的第一个顶点为源点,最后一个顶点为终点。
为了操作方便,首先使用面向对象的方法,来实现一个加权的有向图,其Java代码如下:
/**
* 有向边
*/
public class Edge{
private final int from;
private final int to;
private final int weight;
public Edge(int from, int to, int weight) {
super();
this.from = from;
this.to = to;
this.weight = weight;
}
public int getFrom() {
return from;
}
public int getTo() {
return to;
}
public int getWeight() {
return weight;
}
}
//带权有向图的实现
public class WeightedDigraph {
private final int vertexsNum;
private final int edgesNum;
private List[] adj; //邻接表
public WeightedDigraph(int[][] data, int vertexsNum) {
this.vertexsNum = vertexsNum;
this.edgesNum = data.length;
adj = (List[]) new ArrayList[vertexsNum];
for(int i=0; i();
}
for (int i = 0; i < data.length; i++) {
Edge edge = new Edge(data[i][0],data[i][1],data[i][2]);
int v = edge.getFrom();
adj[v].add(edge);
}
}
public Iterable adj(int vertex) {
return adj[vertex];
}
public int getVertexsNum() {
return vertexsNum;
}
public int getEdgesNum() {
return edgesNum;
}
//有向图中所有的边
public Iterable getEdges() {
List edges = new ArrayList<>();
for(List list : adj) {
for(Edge e : list) {
edges.add(e);
}
}
return edges;
}
} 5.1、Dijkstra(迪杰斯特拉)算法:
计算的是一个点到其余所有点的最短路径。
算法思想: 如果点 i 到点 j 的最短路径经过k,则ij路径中,i到k的那一段一定是i到k的最短路径。
查找方法:
(1)声明2个一维数组:一个用来标识当前顶点是否已经找到最短路径。另一个数组用来记录v0到该点的最短路径中,该点的前一个顶点是什么。
(2)比较:计算v0到vi的最短路径时,比较v0vi与v0vk+vkvi的大小,而v0vk与vkvi的值是暂时得出的记录在数组中的最短路径。
//Dijkstra算法的实现
public class Dijkstra {
private Edge[] edgeTo; //最短路径树
private int[] distTo; //存储每个顶点到源点的距离
//索引优先队列,建立distTo和顶点索引,distTo越小,优先级越高
private IndexMinPQ pq;
public Dijkstra(WeightedDigraph wd, int s) {
edgeTo = new Edge[wd.getVertexsNum()];
distTo = new int[wd.getVertexsNum()];
pq = new IndexMinPQ<>(wd.getVertexsNum());
for(int i=0; i distTo[ver] + e.getWeight()) {
distTo[v] = distTo[ver] + e.getWeight();
edgeTo[v] = e;
if(pq.contains(v)) {
pq.change(v, distTo[v]);
}else {
pq.insert(v, distTo[v]);
}
}
}
}
} Dijkstra算法的局限性:图中边的权重必须为正,但可以是有环图。时间复杂度为O(ElogV),空间复杂度O(V)。
5.2、Floyd(弗洛伊德)算法
弗洛伊德与Dijkstra算法的区别:
(1)它们都是基于比较v0vi与v0vk+vkvi的大小的基本算法。
(2)弗洛伊德三次循环计算出了每个点个其他点的最短路径,Dijkstra算法用2次循环计算出了一个点到其他各点的最短路径 。
(3)如果要计算出全部的点到其他点的最短路径,他们都是O(n^2)
有兴趣的朋友可以了解一下。
图的算法很多,难以尽树,至今还有以下内容没有总结:
-
图的邻接多重表
-
图的边集数组实现
-
最短路径的Floyd算法
-
拓扑排序
-
union-find算法
-
无环加权有向图的最短路径算法
-
关键路径
-
计算无向图中连通分量的Kosaraju算法
-
有向图中含必经点的最短路径问题
-
TSP问题
-
还有A*算法
先到这,最后感谢前辈的博客:
数据结构与算法(六),图
数据结构(七)图