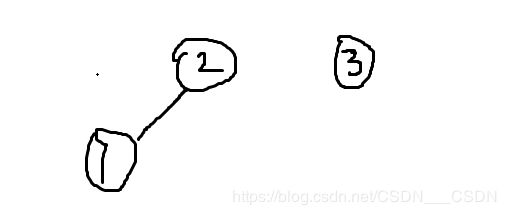【HDU】3635 Dragon Balls （带权并查集 一）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3635

【问题描述】

有标号为1到n的n个龙珠，分别放在对应标号为1到n的n个城市里。 
下面有两种操作: 
T A B表示把A龙珠所在城市的所有龙珠都转移到B龙珠所在的城市中 
Q A 表示查询A，需要知道A龙珠现在所在的城市，A所在的城市有几颗龙珠，A转移到这个城市移动了多少次,分别输出3个整数，表示上述信息。

【输入描述】

第一行一个整数T表示测试数据组数T∈[0,100] 
对于每一组测试数据，第一行包含两个整数N,Q∈[2,10000] 
接下来Q行，每行包含如下的操作或询问：T A B或Q A，如题目描述所示。

【输出描述】

对于每一组测试数据，先输出一行Case x:(x表示测试数据标号，从1开始)，然后对于每一个询问，输出一行三个数表示答案，用空格隔开

【样例输入】

2
3 3 
T 1 2 
T 3 2
Q 2
3 4 
T 1 2
Q 1
T 1 3 
Q 1

【样例输出】

Case 1:
2 3 0
Case 2:
2 2 1 
3 3 2

 

开三个数组

pre数组：pre[i]表示第i个球所在的城市

sum数组：sum[i]表示第i个城市所拥有的球的个数

cnt数组：cnt[i]表示第i个球移动了几次

init()：初始化，每一个球原来都呆在自己的城市，所以每一个城市里都只有1个球，每一个球的移动次数都是0。

如果输入的是T，x，y，则find函数找到x和y的根结点，在find函数递归的时候，先是一直延伸向下，找到它的根结点fx，然后在回溯的过程中修改cnt数组（即cnt[i]表示第i个球移动的次数）以及进行压缩路径。

某一个球移动的次数 = 他自己移动的次数 + 它上面的根结点移动的次数 ，所以find(pre[x])一直延伸向上找到最高的那一个点，然后再回溯的过程中加上每一个根结点移动的次数，逐个加上，涉及到的点都要进行路径压缩，把相应的点连接到fx上

举个例子：

一组测试数据：

3 4
T 1 2
Q 1
T 1 3
Q 1

第一步：

sum[1] = 1     cnt[1] = 0     pre[1]=1

sum[2] = 1     cnt[2] = 0     pre[2]=2

sum[3] = 1     cnt[3] = 0     pre[3]=3

 

第二步

在join函数中，find函数没有进行递归，直接返回，fx=1，fy=2，1连到2上，fx（就是x，也就是1）为根结点，移动次数被置为1，pre[1] = 2

 

第三步：

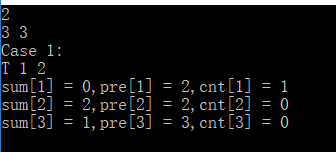
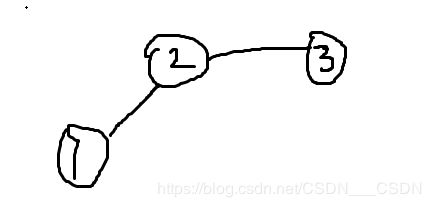
再次连接的时候，y=3，在调用find函数的时候，直接返回fy=3。但是，x=2，是先一直递归得到fx=2，回溯，退回到x=1，pre[1]=2，cnt[1] += cnt[2]，这时候的cnt[2]=0，路径压缩，pre[1]=2，返回2给fx。之后pre[2] =3（得到的状态如上面那幅图所示，将1的根结点连接到3，用题目中的话来说就是将1所在的城市的所有龙珠转移到3城市中，所以3所在的城市的龙珠数量要加上1所在的城市的龙珠的数量，这是1和2在一个城市，之后因为都移走了，所以要置0），sum[3]+=sum[2]，sum[2]=0。移动的那个根结点cnt的值置为1。

第四步：

在主函数中，假设要查找的结点是a，root来接受find(a)的值，在调用find函数的同时会进行路径压缩，图的状态会变成上面那种样子，先是x=3，直接返回3给fx，这是x=2了，cnt[2]+=cnt[3]（cnt[3]=0，因为没有移动过），pre[2]=3，在返回3给fx，这时候x=1，cnt[1]+=cnt[2]，所以cnt[1]变成了2，pre[1]=3，（fx一直接受的返回值都是3），所以，1也连接到3上去了。在最后的输出中，注意保存要查找的根结点就好，前两个输出的数都是要按照根结点来找的，最后一个是根据结点的序号去找的。

只要递归遍历到的点，都会直连到该集合的根节点下，如果遍历到的点还有子树，但是子树上的结点不涉及在这一次递归中，那么就直接一整棵子树连接到该集合的根节点上去。

在回退的过程中，一开始找到的fx（即那个集合的根结点）一直保存在fx中，就是为了pre[x]=fx。

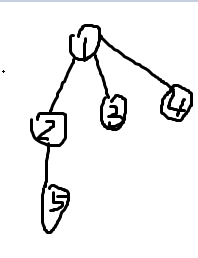
例如要创建的是这样的一棵树，为了看出路径压缩的过程，我们在输入数据的时候，要从下网上输入。

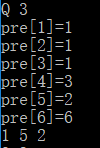
Q 1

     

还是这一种状态，pre[1] = 1，之前都是其他的点的移动，最后是连接到1上，1没有移动过

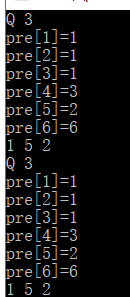
Q 3

    

 

在递归的过程中，3，2，1，接着回溯，所以这三个点，最后都会路径压缩，直接连接到1上，像2和3还连接着其他子树，就直接一起，以2和3为根一起带过去了。

之后再Q 3 ，也不会发生改变了，因为已经路径压缩完成，是当前的最优状态了。

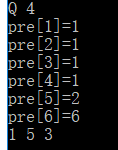
之后再试一下Q 4

     

（现在大家可以体会到递归以及路径压缩是怎么一回事了吗）

#include 
#include 
#include 

using namespace std;

const int maxn = 10005;

int pre[maxn];
int sum[maxn];
int cnt[maxn];
int n,m,root;
char str[3];

void init()
{
	for(int i=0;i