1. 什么是最大流问题?
首先要先清楚最大流的含义,就是说从源点到经过的所有路径的最终到达汇点的所有流量和。
流网络G=(V,E)是一个有向图,其中每条边(u,v)∈E均有一个非负容量c(u,v)>=0。如果(u,v)不属于E,则假定c(u,v)=0。流网络中有两个特别的顶点:源点s和汇点t。下图展示了一个流网络的实例(其中斜线左边的数字表示实际边上的流,右边的数字表示边的最大容量):
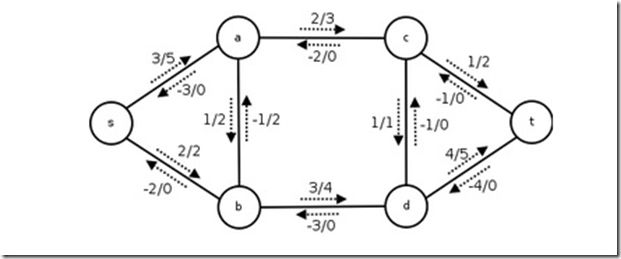
2.基础概念
容量网络:设G(V,E),是一个有向网络,在V中指定了一个顶点,称为源点(记为Vs),以及另一个顶点,称为汇点(记为Vt);对于每一条弧属于E,对应有一个权值c(u,v)>0,称为弧的容量.通常吧这样的有向网络G称为容量网络.
弧的流量:通过容量网络G中每条弧,上的实际流量(简称流量),记为f(u,v);
网络流: 所有弧上流量的集合f={f(u,v)},称为该容量网络的一个网络流.
可行流: 在容量网络G中满足以下条件的网络流f,称为可行流.
a.弧流量限制条件: 0<=f(u,v)<=c(u,v);
b. 斜对称性:f(u,v) = -f(v,u)
c:平衡条件:即流入一个点的流量要等于流出这个点的流量,(源点和汇点除外).
若网络流上每条弧上的流量都为0,则该网络流称为零流.
伪流: 如果一个网络流只满足弧流量限制条件,不满足平衡条件,则这种网络流为伪流,或称为容量可行流.(预流推进算法有用)
最大流: 在容量网络中,满足弧流量限制条件,且满足平衡条件并且具有最大流量的可行流,称为网络最大流,简称最大流.
弧的类型:
a.饱和弧:即f(u,v)=c(u,v);
b.非饱和弧:即f(u,v)
c.零流弧:即f(u,v)=0;
d.非零流弧:即f(u,v)>0.
链:在容量网络中,称顶点序列(u1,u2,u3,u4,…,un,v)为一条链要求相邻的两个顶点之间有一条弧.
设P是G中一条从Vs到Vt的链,约定从Vs指向Vt的方向为正方向.在链中并不要求所有的弧的方向都与链的方向相同.
a.前向弧:(方向与链的正方向一致的弧),其集合记为P+,
b.后向弧:(方向与链的正方向相反的弧),其集合记为P-.
增广路:
设f是一个容量网络G中的一个可行流,P是从Vs到Vt 的一条链,若P满足以下条件:
a.P中所有前向弧都是非饱和弧,
b.P中所有后向弧都是非零弧.
则称P为关于可行流f 的一条增广路.
沿这增广路改进可行流的操作称为增广.
残留容量:残留容量的定义为:cf(u,v)=c(u,v)-f(u,v)。而由所有属于G的边的残留容量所构成的带权有向图就是G的残留网络。下图就是上面的流网络所对应的残留网络:
对应

残余网络为:
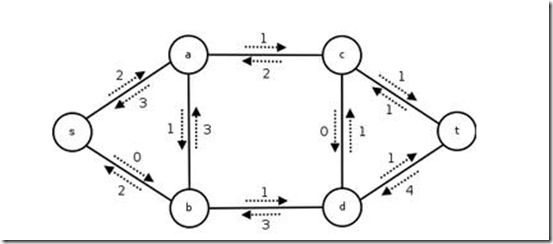
在一个连通图中,如果删掉若干条边,使图不联通,则称这些边为此图的一个割集。在这些割集中流量和最小的一个称为最小割。
最大流最小割定理:一个图的最大流等于最小。 https://www.cnblogs.com/TreeDream/p/5929429.html
增广路径
增广路径算法的思想是每次从源点出发找到一条到达汇点的可行路径,那么从源点到汇点的网络流至少可以增加w(w为这条路径上的边的最小容量)。此时,将最大流增加w,这条路径称为增广路径,同时从源到汇沿着增广路径将经过的每条正向边(从源指向汇)的流量都减去w,并将每条边的反向边的流量加上w。这个操作就为增广操作。
不断的进行增广操作,直到无法从源到达汇停止。那么,此时得到最大流的流量。同时,可以得到在获得最大流的时候,每条边上的流量分布(只需要将原图中每条边的容量减去最后的残余网络中每条边对应的流量即可)
反向边
下面是所有最大流算法的精华部分:引入反向边
为什么要有反向边呢?

我们第一次找到了1-2-3-4这条增广路,这条路上的delta值显然是1。于是我们修改后得到了下面这个流。(图中的数字是容量)

这时候(1,2)和(3,4)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是1。
但这个答案明显不是最大流,因为我们可以同时走1-2-4和1-3-4,这样可以得到流量为2的流。
那么我们刚刚的算法问题在哪里呢?问题就在于我们没有给程序一个”后悔”的机会,应该有一个不走(2-3-4)而改走(2-4)的机制。那么如何解决这个问题呢?回溯搜索吗?那么我们的效率就上升到指数级了。
而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边(I,j)都有一条反向边(j,i),反向边也同样有它的容量。
我们直接来看它是如何解决的:
在第一次找到增广路之后,在把路上每一段的容量减少delta的同时,也把每一段上的反方向的容量增加delta。即在Dec(c[x,y],delta)的同时,inc(c[y,x],delta)
我们来看刚才的例子,在找到1-2-3-4这条增广路之后,把容量修改成如下
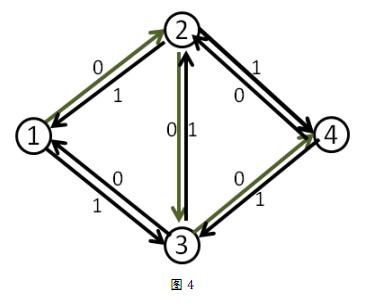
这时再找增广路的时候,就会找到1-3-2-4这条可增广量,即delta值为1的可增广路。将这条路增广之后,得到了最大流2。
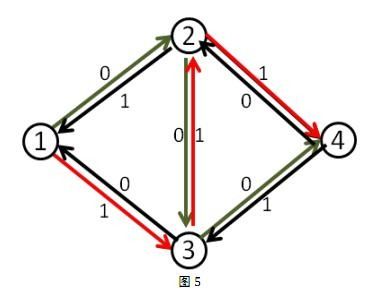
那么,这么做为什么会是对的呢?我来通俗的解释一下吧。
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给”退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。(有人问如果这里没有2-4怎么办,这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点)同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流量。
这就是这个算法的精华部分,利用反向边,使程序有了一个后悔和改正的机会
3. 算法介绍
-
Fold-Fulkerson算法
Fold-Fulkerson算法就是朴素的增广路径思想。
求最大流的过程,就是不断找到一条从源到汇的路径,然后构造残余网络,再在残余网络的基础上寻找新的路径,使总流量增加,然后形成新的残余网络,在寻找新路径… 直到某个残余网络上找不到从源到汇的路径为止。
每用DFS执行一次找路径,增广的操作,都会使得最大流增加,假设最大流为C,那么时间复杂度可以达到 C*(m+n), m为边的数目,n为顶点的数目。
-
Edmonds-Karp算法
O(N * M^2)
Edmonds-Karp算法是在Fold-Fulkerson思想上进行改进:
每次寻找增广路径的时候,总是寻找一条从源到汇经过节点数目最少的路径,即最短路径。这是一种“最短增广路径” Shortest Augmenting Path(SAP)的算法。
在实现的时候,每次利用BFS搜索,找到一条从源到汇的最短路径,然后进行增广操作;再进行BFS…直到无法找到从源到汇的路径为止。
时间复杂度可以达到 nmm, n为顶点的数目,m为边的数目。
-
dinic算法
O(n^2 * m)
Dinic算法最核心的内容就是多路增广!!!,划重点。
沿着EK算法的过程:

我们有一个图,如图一。
按照套路,我们先BFS,找S−T最短路。所有的距离标号都画在了图二上(EK算法可能用不到,但Dinic得到)。
假设我们选的是S−3−T这条路,增广。。。(如图三,绿色)
然后我们再来一遍BFS。。。 等等!
细心的你可能也发现了,S−1−T也是一条S−T最短路。
那就增广吧!(如图四)
您可以检查一下,这时候没有长度为2的最短路了。
但EK算法不会这样。它会再笨拙地从头再BFS一遍,这就浪费了不少时间。
所以说,多路增广是很重要的。
-
ISPA算法
http://www.renfei.org/blog/isap.htm
复杂度分析:https://www.cnblogs.com/owenyu/p/6852664.html
ISAP算法为优化的最短增广路径算法(Improved Shortest Augmenting Path)。相比Dinic,ISAP算法不需要在回溯到源点之后再次进行BFS分层操作,而是在DFS以及回溯的过程中就进行了节点的重标号(即分层操作);以及ISAP算法进行gap优化大大提升效率。
具体流程为:
1----- 定义dist[v] 为点v到达汇点的距离(即经过几个点到达汇点),定义gap[d]在当前残余网络中到达汇点(经过路径上流量不能为0)距离为d的点的个数。
2-----从汇点到源点进行反向BFS,标记下每个节点到达汇点的最短距离,即和Dinic算法相反的分层操作。
3----- 当前点u从源点出发,用DFS找到一条到达汇点的路径…
4----- 若点u为汇点,则找到了一条增广路径,进行增广操作;若点u可以向前走到v,且u–>v为一条可行边(dist[u] = dist[v]+1,且边u–>v流量不为0),则u走到v;若u无法向前推进到任何点,则对u进行重标号,然后回溯u到原来的增广路径中上一个点 pre[u].
5------ 在重标号和回溯之前,可以进行gap优化。gap[d]在当前残余网络中到达汇点(经过路径上流量不能为0)距离为d的点的个数。 若从u无法找到一条可行边,则表明可以经过 dist[u] 条边到达汇点的点数目少了一个,即 gap[dist[u]] --。若此时 gap[dist[u]] = 0,则说明当前残余网络中,没有任何一个点可以经过dist[u]条边到达汇点,源点到汇点的距离肯定大于等于dist[u],若源点能够到达汇点,那么要求源点到汇点的路径中肯定有到达汇点距离为dist[u]的点,所以,无法从源点到达汇点此时,可以直接返回结果。
-
重标号,是将点u重新分层,重新设置点u经过不为0的边可达汇点的最短距离。具体是 dist[u] = min{dist[v]|u连接到v,且u–>v边流量不为0} + 1. 若从u出发的边流量均为0,则无法找到下一个点,则直接将dist[u]置为n(n为节点个数),这样就说明u点不可达。
优化:
1----- GAP优化:
如果一次重标号时,出现距离断层即Gap[i] = 0,则可以证明ST无可行流,此时则可以直接退出算法。
2----- 当前弧优化:
为了使每次找增广路的时间变成均摊O(V),还有一个重要的优化是对于每个点保存“当前弧”:初始时当前弧是邻接表的第一条弧;在邻接表中查找时从当前弧开始查找,找到了一条允许弧,就把这条弧设为当前弧;改变距离标号时,把当前弧重新设为邻接表的第一条弧。
小结:
增广路算法核心都是一样的:寻找增广路径,更新路径上的流量(残余网络),直到找不到可行流。
在寻找增广路径上,EK最笨拙,每次bfs只找一条增广路径,Dinic每次bfs分层后的dfs可能找到多条增广路径,因此在稠密图中dinic要远好于EK。ISPA除了刚开始的bfs分配距离标号外,其他操作都是dfs+重标号,交错进行,直到出现断层。
代码:
hdu1532
EK:
// 最大流 EK
#include
#include
#include
#include
#include
#define fi first
#define se second
#define pii pair
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;
const int maxn = 200+5;
int n;
// 图
struct Edge{
int u, v, cap, flow;
Edge(int a, int b, int c, int d):u(a),v(b),cap(c),flow(d){}
};
vector edges;
vector G[maxn];
int asc[maxn]; // 从起点到i的可改进量
int p[maxn]; // 最短路树上p的入弧编号
void init(){
for(int i = 0; i < maxn; ++i) G[i].clear();
edges.clear();
}
void addEdge(int u, int v, int cap){
edges.push_back(Edge(u,v,cap,0));
edges.push_back(Edge(v,u,0,0)); // 反向弧
int m = edges.size();
G[u].push_back(m-2);
G[v].push_back(m-1);
}
// 最大流
int MaxFlow(int s, int t){
int flow = 0;
while(1){
memset(asc, 0, sizeof(asc));
asc[s] = INF;
queue Q;
Q.push(s);
while(!Q.empty()){
int x = Q.front(); Q.pop();
for(int i = 0; i < G[x].size(); ++i){ // 枚举 x->
Edge e = edges[G[x][i]];
if(0 == asc[e.v]&&e.cap > e.flow){
p[e.v] = G[x][i];
asc[e.v] = min(asc[x], e.cap-e.flow);
Q.push(e.v);
}
}
if(asc[t]) break;
}
if(0 == asc[t]) break; // 找不到增广路径了
// 找到一条增广路径,更新流量
for(int u = t; u != s; u = edges[p[u]].u) {
edges[p[u]].flow += asc[t];
edges[p[u]^1].flow -= asc[t];
}
flow += asc[t];
}
return flow;
}
int main()
{
freopen("in.txt","r",stdin);
int n, m;
while(scanf("%d%d",&m,&n) == 2&&n){
init();
for(int i = 0; i < m; ++i){
int a,b,c; scanf("%d%d%d",&a,&b,&c);
addEdge(a-1,b-1,c);
}
int ans = MaxFlow(0, n-1);
printf("%d\n", ans);
}
return 0;
}
Dinic:
// 最大流 dinic算法
#include
#include
#include
#include
#include
#define fi first
#define se second
#define pii pair
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;
const int maxn = 200+5;
int n;
// 图
struct Edge{
int u, v, cap, flow;
Edge(int a, int b, int c, int d):u(a),v(b),cap(c),flow(d){}
};
vector edges;
vector G[maxn];
int dis[maxn]; // 分层的编号
void init(){
for(int i = 0; i < maxn; ++i) G[i].clear();
edges.clear();
}
void addEdge(int u, int v, int cap){
edges.push_back(Edge(u,v,cap,0));
edges.push_back(Edge(v,u,0,0)); // 反向弧
int m = edges.size();
G[u].push_back(m-2);
G[v].push_back(m-1);
}
// 分层
bool bfs(int s, int t){
memset(dis, -1, sizeof(dis));
dis[s] = 0;
queue Q;
Q.push(s);
while(!Q.empty()){
int x = Q.front(); Q.pop();
for(int i = 0; i < G[x].size(); ++i){
Edge e = edges[G[x][i]];
if(dis[e.v] == -1&&e.cap > e.flow){
dis[e.v] = dis[x] + 1;
Q.push(e.v);
}
}
}
return dis[t] != -1;
}
int dfs(int s, int t, int cur_flow){
if(s == t||cur_flow == 0) return cur_flow;
int ans = 0;
for(int i = 0; i < G[s].size(); ++i){
int c = G[s][i];
Edge e = edges[c];
if(dis[e.v] == dis[s] + 1&&e.cap > e.flow){
int a2 = min(cur_flow, e.cap-e.flow);
int w = dfs(e.v, t, a2);
edges[c].flow += w;
edges[c^1].flow -= w;
cur_flow -= w;
ans += w;
if(cur_flow <= 0) break;
}
}
return ans;
}
int Dinic(int s, int t){
int ans = 0;
while(bfs(s,t)){
ans += dfs(s,t,INF);
}
return ans;
}
int main()
{
freopen("in.txt","r",stdin);
int n, m;
while(scanf("%d%d",&m,&n) == 2&&n){
init();
for(int i = 0; i < m; ++i){
int a,b,c; scanf("%d%d%d",&a,&b,&c);
addEdge(a-1,b-1,c);
}
int ans = Dinic(0, n-1);
printf("%d\n", ans);
}
return 0;
}
ISPA:
#include
#include
#include
#include
#include
#define fi first
#define se second
#define pii pair
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;
const int maxn = 200+5;
// 图
struct Edge{
int u, v, cap, flow;
Edge(int a, int b, int c, int d):u(a),v(b),cap(c),flow(d){}
};
vector edges;
vector G[maxn];
int n, m;
int dis[maxn]; // 分层,从汇点 -> 源点
int pre[maxn]; // 可增广路上的上一条弧的编号
int Gap[maxn]; // 距离汇点最短距离为 i 的点有多少个
int cur[maxn]; // 当前弧下标. (优化)
void init(){
for(int i = 0; i < maxn; ++i) G[i].clear();
edges.clear();
}
void addEdge(int u, int v, int cap){
edges.push_back(Edge(u,v,cap,0));
edges.push_back(Edge(v,u,0,0)); // 反向弧
int m = edges.size();
G[u].push_back(m-2);
G[v].push_back(m-1);
}
// 从(汇点)t -> s(源点),反向bfs建立距离标号d , 并统计Gap[d]
void bfs(int s, int t){
memset(dis, -1, sizeof(dis));
memset(Gap, 0, sizeof(Gap));
dis[t] = 0;
Gap[0] = 1;
queue Q;
Q.push(t);
while(!Q.empty()){
int x = Q.front(); Q.pop();
for(int i = 0; i < G[x].size(); ++i){
Edge e = edges[G[x][i]^1];
if(dis[e.u] == -1){
dis[e.u] = dis[x] + 1;
++Gap[dis[e.u]];
Q.push(e.u);
}
}
}
}
// 增广
int augument(int s, int t){
int min_flow = INF;
// 从汇点到源点通过 p 追踪增广路径, df 为一路上最小的残量
for(int u = t; u != s; u = edges[pre[u]].u){
Edge e = edges[pre[u]];
min_flow = min(min_flow, e.cap - e.flow);
}
// 从汇点到源点更新流量
for(int u = t; u != s; u = edges[pre[u]].u){
edges[pre[u]].flow += min_flow;
edges[pre[u]^1].flow -= min_flow;
}
return min_flow;
}
int ISPA(int s, int t){
bfs(s, t);
memset(cur, 0, sizeof(cur));
int u = s;
int ans = 0;
while(dis[s] < n){
if(u == t){
ans += augument(s, t);
u = s;
}
// 寻找可行弧,看是否可以前进
bool advanced = false;
for(int i = cur[u]; i < G[u].size(); ++i){
Edge e = edges[G[u][i]];
if(dis[u] == dis[e.v] + 1&&e.cap > e.flow){
advanced = true;
pre[e.v] = G[u][i];
cur[u] = i; // 记录节点u访问到哪一条弧了,下次接着访问
u = e.v; // 前进到下一个点
break;
}
}
// 节点u找不到可行弧,回退.
if(!advanced){
// 改变 u 的距离标号为所有u->v中d[v]的最小值+1
int d1 = n-1;
for(int i = 0; i < G[u].size(); ++i){
Edge e = edges[G[u][i]];
if(e.cap > e.flow)
d1 = min(d1, dis[e.v]);
}
if(--Gap[dis[u]] == 0) break; // 一旦发现某个距离值没有对应的点了,结束
dis[u] = d1 + 1;
++Gap[dis[u]];
cur[u] = 0;
if(u != s) u = edges[pre[u]].u; // 回退到弧尾
}
}
return ans;
}
int main()
{
freopen("in.txt","r",stdin);
while(scanf("%d%d",&m,&n) == 2&&n){
init();
for(int i = 0; i < m; ++i){
int a,b,c; scanf("%d%d%d",&a,&b,&c);
addEdge(a-1,b-1,c);
}
int ans = ISPA(0, n-1);
printf("%d\n", ans);
}
return 0;
}
参考: https://blog.csdn.net/x_y_q_/article/details/51999466 ,
https://www.cnblogs.com/qiucz/p/4601241.html,
https://blog.csdn.net/vonmax007/article/details/64921089






