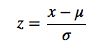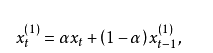回归模型——波士顿房价数据集(《python 深度学习》)
1 数据集简介与数据的分析
1.1 数据背景简介
波士顿房价数据集是统计的20世纪70年代中期波士顿郊区房价的中位数,统计了当时教区部分的犯罪率、房产税等共计13个指标,统计出房价,试图能找到那些指标与房价的关系。本例子明显的是属于回归模型的案例。在数据集中包含506组数据,其中404是训练样本,剩下的102组数据作为验证样本。
1.2 数据结构的分析
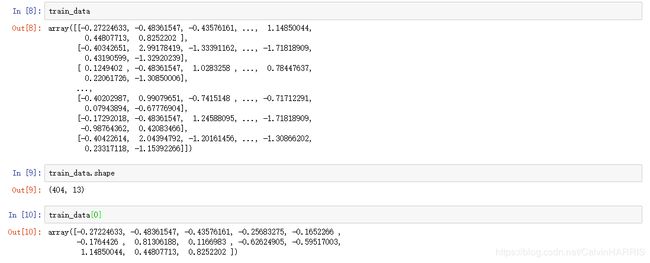
先来看看数据集的数据结构,输入
from keras.datasets import boston_housing
(train_data,train_targets),(test_data,test_targets) = boston_housing.load_data()如图所示整个训练集的结构是一个403*13的矩阵列表,每一行代表一组指标。随机打开第一组数据,发现数据并没有一个明显的特征,比如说都在0~1之间,而事实上,这些指标的取值范围有很大的差异,有的取值范围是0~1有的是0~100等等,差异巨大。因此我们在数据输入之前应当将数据做归一化处理。
2 数据的预处理
2.1 0均值标准化(Z-score standardization)
所谓数据的归一化就是将数据“去量纲化”,这是一个物理学的概念,简单来说我们就是要把这些数据指标的单位的影响去掉,使得他们都在同一个量纲上——无量纲上进行讨论,这样数据之间的相互关系还在,其他的一些干扰因素就少了很多。归一化基本方法有线性函数归一化与0均值标准化两种(详见https://blog.csdn.net/zbc1090549839/article/details/44103801),在数据大致呈现正态分布的前提下一般采用0均值标准化(Z-score standardization),公式为
含义就是将数据减去数据组的平均数再除以标准差,这样处理后每项指标数据均成平均值为0,标准差为1的正态分布。代码实现如下:
(train_data,train_targets),(test_data,test_targets) = boston_housing.load_data()
mean = train_data.mean(axis = 0)
train_data -= mean
std = train_data.std(axis = 0)
train_data /= std
test_data -= mean
test_data /= std这里要着重注意的是,对测试数据的处理使用的平均值和标准差都是训练集的,绝对不可以动用测试集的任何数据做任何脱离训练集的处理。
3 构建网络
3.1 模型定义
def build_model():
model = models.Sequential()
model.add(layers.Dense(64,activation = 'relu',input_shape = (train_data.shape[1],)))
model.add(layers.Dense(64,activation = 'relu'))
model.add(layers.Dense(1))
model.compile(optimizer = 'rmsprop',loss = 'mse',metrics = ['mae'])
model.summary()
return model因为数据很少,因此没有把网络设计的过于复杂,在本例中设置一个隐藏层,输入层和隐藏层节点数均为64,激活函数选用relu最后一层不设激活函数,因为本例是一个回归问题,输出数据不能限制他的范围。编译模型中,优化器选用rmsprop,损失函数用均方差,就是预测值与实际值差的平方,在回归问题常采用。监控器的指标是平均绝对误差(MAE)就是实际值与预测值的差的绝对值。
3.2 k-折交叉检验
在之前的案例中由于训练集都是有着上万的数据,我们可以拿出其中一两千组数据来作为验证集而不影响训练的精度,在本例中,训练集的数目只有404个倘若拿出20%数据来验证,因为数据量的因素,选用不同的20%数据可能会得到相差较大的方差,从而很难从中评估模型的好坏。因此我们在这里使用k折交叉验证来使得验证的指标相对可靠。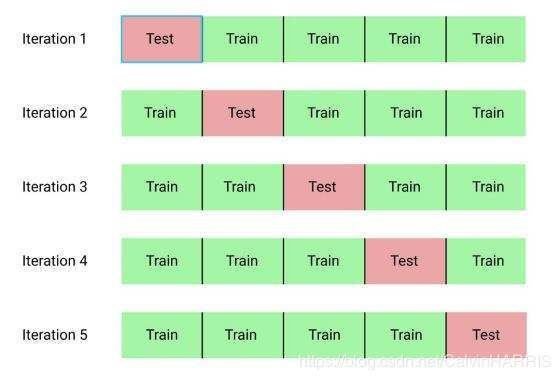
如上图所示,所谓的K折就是把数据集分成K份,在其中的K-1份上做Training剩下的做Validation,然后取K个验证集的平均值作为最后的评估。代码实现如下
num_val_samples = len(train_data) // k #a//b的含义就是取整
for i in range(k):
print('processing fold#',i)
val_data = train_data[i*num_val_samples:(i+1)*num_val_samples]
val_targets = train_targets[i*num_val_samples:(i+1)*num_val_samples]
partial_train_data = np.concatenate([
train_data[:i*num_val_samples],train_data[(i+1)*num_val_samples:]],axis = 0)
partial_train_targets = np.concatenate([
train_targets[:i*num_val_samples],train_targets[(i+1)*num_val_samples:]],axis = 0)
这里的函数np.concatenate实现的是两个矩阵的连接,axis = 0就是按矩阵的0维(就是列,行是1维)连接起来。
4 网络训练与结果分析
4.1 模型训练
网络训练是在每个K折后进行的,例如数据分成4折(上图的lteration),在其后面进行模型的训练。代码如下:
all_mae_histories = []
model = build_model()
history = model.fit(partial_train_data,partial_train_targets,
validation_data = (val_data,val_targets),
epochs = num_epochs,batch_size = 1,verbose = 0)
mae_history = history.history['val_mean_absolute_error']
all_mae_histories.append(mae_history)这里我们把model.fit返回的对象history 中的字典键值val_mean_absolute_error的值储存到列表all_mae_histories中,为后面的绘图分析做准备。
4.2 绘图分析
4.2.1 绘图数据准备
在绘图之前我们需要将数据做整理。要衡量的指标肯定是MAE,必定也是看与epchs之间的关系,那么怎样才能找出每次循环下的MAE呢,前面提到K折交叉验证采用的就是每次Val上的平均值,那么这个怎么求出来呢?先看一下之前创建的all_mae_histories列表在学习后的内容。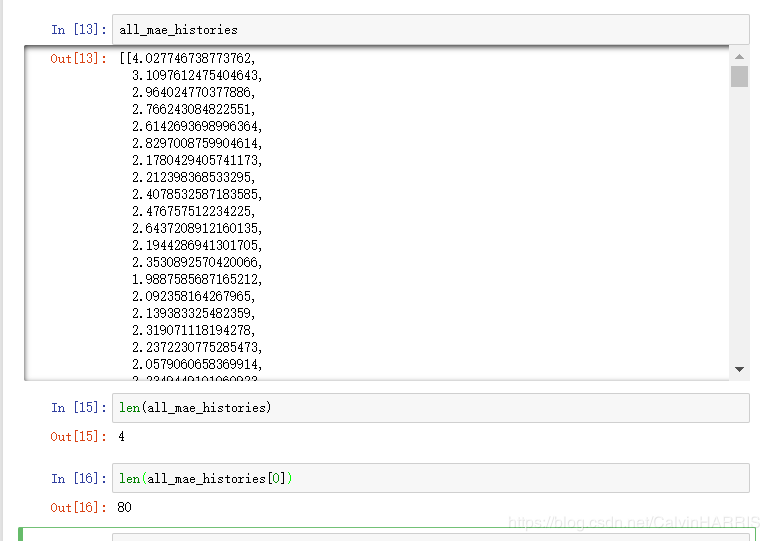
可以看到,得到的是4个列表,每个列表有80个元素(这里epchs值为80是下面分析优化后的),对应着4折和循环次数。把他想象成一个矩阵,那么他就是一个4*80的矩阵,矩阵对应的每一列就是那次循环的4个折的val_mae值,我们要算的就是对应列的平均值。代码如下:
average_mae_history = [np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]首先我们返回的肯定要是一个列表,为后面的作图做准备,其次,要算平均值用到np.mean函数,肯定要构造一个numpy数组,这就是括号里方括号的含义。这里用到了python的链式结构(说法不一定正确),它在一行就是并列的,在括号里的for实现的是取四个折,然后后面的for就是逐列求mean。操作顺序就是先把第x个数组取出来,取他的第i个元素,再取第x+1个数组的第i个元素一直取到第4个数组的第i个元素为止求一次mean,随后再取第x个数组的第i+1个元素......以此类推。最后返回的就是每次epchs的val平均值。
4.2.2 绘图分析
plt.plot(range(1,len(average_mae_history)+1),average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
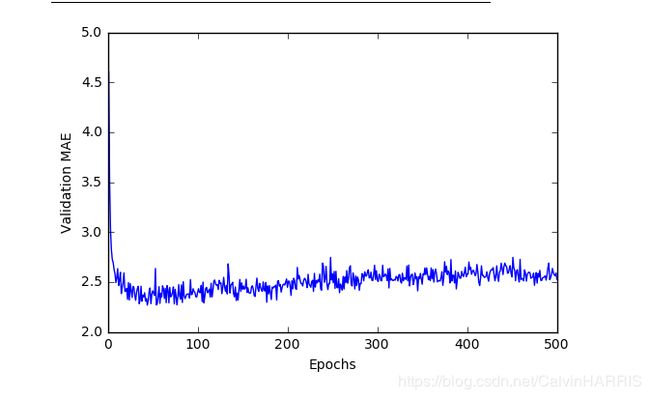
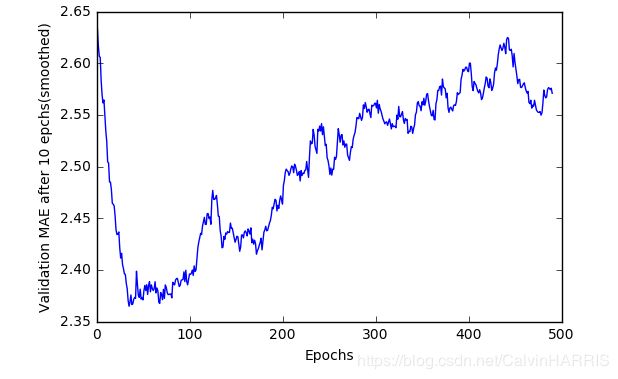
plt.show()图像如下(尚未分析优化-epchs为500):
如图,点与点之间的距离过于靠近,难以判断大约10次epchs后的微观的趋势,也就是很难找到一个大概的最小的MAE值,因此我们考虑对图像做如下处理:
- 将前十个点去掉,因为其与其他的点范围相差过大。
- 将折线尽量平滑。
第一点比较容易实现,第二点就需要用到数学上的指数滑动平均法来实现,所谓的指数滑动平均法就是利用上一期的实际值和预测值(估算值),对它们进行不同的加权分配,求得一个指数平滑值,作为下一期预测值的一种预测方法。它能用上一个数值预测下一个数值,使得相邻两个数值之间的关系不会显得那么突兀,所谓的“指数”就是两个数据之间的关联度。如下公式:
alpha就是关联度指数,我们在这里将其设置为0.1,代码如下:
def smooth_curve(points,alpha = 0.9):
smothed_points = []
for point in points:
if smothed_points:
pre_point = smothed_points[-1]
smothed_points.append ((pre_point*alpha + point*(1- alpha)))
else:
smothed_points.append(point)
return smothed_points
smooth_mae_history = smooth_curve(average_mae_history[10:])
plt.plot(range(1,len(smooth_mae_history)+1),smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE after 10 epchs(smoothed)')
plt.show()
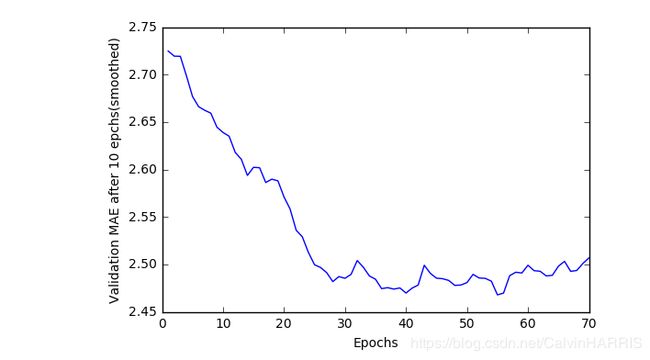
绘图如下:
可以清楚的看到初始迭代设置的是500,大概迭代到80次时MAE达到最低值。随后进入过度拟合。这里看看在验证集上的指标,输入代码:
score = model.evaluate(test_data,test_targets)
print ("The mae score:",score[1])得到mae误差为2.9意味着差距在2900美元左右
修改迭代次数为80(去掉前十个),绘图:
在验证集上的mae值为3.0,并没有改观。随机查看验证集上的预测结果与实际结果:
prediction = model.predict(test_data)
print ("The price that predict:",prediction[77][0])
print ("Actual price:",test_targets[77])输出为:
误差尚可接受。
附主体代码:
from keras.datasets import boston_housing
from keras import models
from keras import layers
import numpy as np
import matplotlib.pyplot as plt
k = 4
num_epochs = 80
#数据归一化处理(Z-score standardization)
(train_data,train_targets),(test_data,test_targets) = boston_housing.load_data()
mean = train_data.mean(axis = 0)
train_data -=mean
std = train_data.std(axis = 0)
train_data /= std
test_data -= mean
test_data /= std
#build model
def build_model():
model = models.Sequential()
model.add(layers.Dense(64,activation = 'relu',input_shape = (train_data.shape[1],)))
model.add(layers.Dense(64,activation = 'relu'))
model.add(layers.Dense(1))
model.compile(optimizer = 'rmsprop',loss = 'mse',metrics = ['mae'])
model.summary()
return model
#k 折验证
num_val_samples = len(train_data) // k
all_mae_histories = []
for i in range(k):
print('processing fold#',i)
val_data = train_data[i*num_val_samples:(i+1)*num_val_samples]
val_targets = train_targets[i*num_val_samples:(i+1)*num_val_samples]
partial_train_data = np.concatenate([
train_data[:i*num_val_samples],train_data[(i+1)*num_val_samples:]],axis = 0)
partial_train_targets = np.concatenate([
train_targets[:i*num_val_samples],train_targets[(i+1)*num_val_samples:]],axis = 0)
model = build_model()
history = model.fit(partial_train_data,partial_train_targets,
validation_data = (val_data,val_targets),
epochs = num_epochs,batch_size = 1,verbose = 0)
mae_history = history.history['val_mean_absolute_error']
all_mae_histories.append(mae_history)
average_mae_history = [np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]
plt.plot(range(1,len(average_mae_history)+1),average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()
def smooth_curve(points,alpha = 0.9):
smothed_points = []
for point in points:
if smothed_points:
pre_point = smothed_points [-1]
smothed_points.append ((pre_point*alpha + point*(1- alpha)))
else:
smothed_points.append(point)
return smothed_points
smooth_mae_history = smooth_curve(average_mae_history[10:])
plt.plot(range(1,len(smooth_mae_history)+1),smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE after 10 epchs(smoothed)')
plt.show()
score = model.evaluate(test_data,test_targets)
print ("The mae score:",score[1])