欧几里德算法(最大公约数算法)
1.欧几里德算法的思想:
欧几里德算法的思想基于辗转相除法的原理,辗转相除法是欧几里德算法的核心思想,欧几里德算法说白了其实就是辗转相除法的计算机算法的实现而已。下面我们先说说辗转相除法,辗转相除法的内容:如果用gcd(a,b)来表示a和b的最大公约数,那么根据辗转相除法的原理,有gcd(a,b)=gcd(b,a mod (b)),其中mod()表示模运算,并且不妨让a>b,这样方便于模运算。
2.辗转相除法的正确性gcd(a,b)=gcd(b,a mod (b))的证明:
第一步:令c为a和b的最大公约数,数学符号表示为c=gcd(a,b).因为任何两个整数的最大公约数c一定是存在的,也就是说必然存在两个数k1,k2使得a=k1.c, b=k2.c
第二步:a mod (b)等价于存在整数r,k3使得余数r=a – k3.b.
即r = a – k3.b
= k1.c – k3.k2.c
= (k1 – k3.k2).c
显然,a和b的余数r是最大公因数c的倍数。
3.欧几里德算法的优点:
通过模运算的余数是最大公约数之间存在的整数倍的关系,来给比较大的数字进行降维,方便手算;同时,也避免了在可行区间内进行全局的最大公约数的判断测试,只需要选取其余数进行相应的计算就可以直接得到最大公约数,大大提高了运算效率。
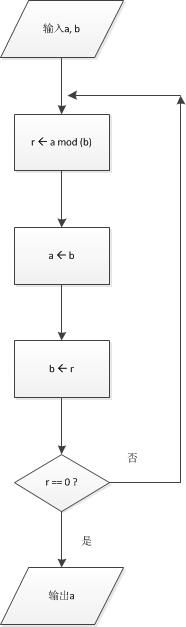
4.欧几里德算法流程图:
5.欧几里德算法的C语言实现:
//功能:利用欧几里德算法,求整数a,b的最大公约数
//参数:整数a,b
//返回:a,b的最大公约数
int gcd(int a, int b){
if(a < b){ //保证a大于等于b,便于a%b的运算
int temp;
temp = a;
a = b;
b = temp;
}
while(a % b){ //如果余数不为0,就一直进行辗转相除
int r = a % b; //r为a和b的余数,即r = a mod(b);
a = b;
b = r;
r = a % b;
}
return b;
}//测试函数
#include
int main(){
printf << gcd(4,12) << endl;
}