数学期望 Expectation
数学期望 Expectation
序言
机器学习中涉及到的很多概念都和 Expectation 相关联,例如:
- 任何分布,我们都关心其 均值 mean、方差 variance、峰度 kurtosis、偏度 skewness;实际上都和数据期望相关;这些内容还和 中心距 以及 泰勒级数 相关联
- 机器学习中,针对模型的泛化能力 Generalization,常见对 泛化误差 decompose 为 Bias(偏差,欠拟合) 和 Variance(方差,过拟合)。这一过程就是利用 Expectation 推导的
- 最大期望算反 EM,明显地和 Expectation 有关联,其是利用了 Expectation 进行推导
所以本文特此明确一下这个基础概念。
期望的定义
The average value of some function f(x) under a probability distribution p(x) is called the expectation of f(x) .
如果 p(x) 是均匀分布的话,我们其实就是求一个函数 f(x) 的平均值而已;如果函数不同的值出现概率不同,我们当然要考虑 p(x) ,来求解真正期望出现的值。标准公式如下(discrete or continuous):
- 期望的操作符号特意用了 E 和一般的 error E 区分开。
- 期望的核心在于函数值分布 p(x) 。其实根据不同的分布我们还能拓展期望的概念,例如 p(x|y) 的条件分布,可以产出 条件期望 conditional expectation;本文不予展开。
- 另外,统计中的 期望,在几何也有对应的 重心,是一个对质量函数的加权积分。
采样 sample
我们不一定能精确地用公式求解出 E[f] ,但我们可以直接对 f(x) 采样,采样得到的值直接求均值 sample mean 来近似出 E[f] (函数期望 约为 函数采样均值 ):
当 N 趋向无穷大,约等于 变为 等于。
运算规则
期望 Expectation 作为一个运算符,有着如下4条运算规则:
(假设 c 为一个常量)
- E(c)=c
- E(cX)=cE(X)
- E(X+Y)=E(X)+E(Y)
- 当 X 、 Y 独立时, E(XY)=E(X)E(Y)
方差与期望
方差本身也可以看作是一个期望,我们依据方差的运算规则,可以等价标准的方差公式如下:
方差 variance E[(f(x)−E[f(x)])2] 也被称为二阶中心距(减去期望 normalize 后对其二次方求期望);其他统计量 偏度 skewness 称为三阶中心距,峰度 kurtosis 四阶中心距。
另外,这里还可以导出一个常用的等价变换公式: E[f(x)2]=VAR[f(x)]+E[f(x)]2
机器学中的 偏差-方差,Bias-Variance
定义
从统计的角度来看,机器学习 中模型的 泛化误差 generalization error 可以 分解 decomposition 为 Bias-Variance 来解释;这里面包含了 Bias-Variance Tradeoff,或者说 Underfitting-Overfitting Tradeoff。
首先再回顾一下俩者概念:
A bias due to the model being too simple
The bias is error from erroneous assumptions in the learning algorithm. High bias can cause an algorithm to miss the relevant relations between features and target outputs (underfitting).
A variance due to the model sensitivity to the data
The variance is error from sensitivity to small fluctuations in the training set. High variance can cause overfitting: modeling the random noise in the training data, rather than the intended outputs.
泛化误差分解
下面的 Figure 1. 中给出了模型泛化时,产生俩种 Errors(Bias,Variance);注意,泛化指的是在测试集上的误差测量,就是衡量模型在之前没有见过的数据上的表现。
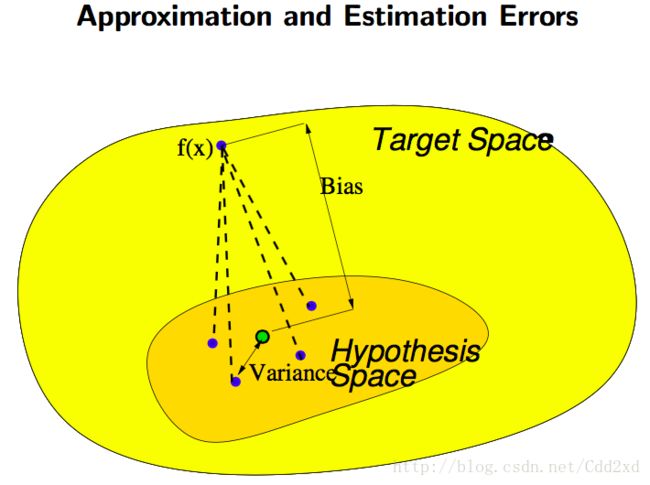
Figure 1. Explanation about Bias-Variance for our models
我们下面通过期望对 泛化误差 进行描述;首先来明确一些本小节相关的符号定义:
- f(x) 表示 true function,表示事物之间真正的规律,这是我们想要逼近的目标
- f(x|w) 表示我们的训练的一个 machine(依据某一个 Dataset)
- Ex 表示我们对整个测试集 求期望
- ED 表示我们对不同数据集 Dataset 训练出来的 machine 求期望
- Eg 表示 泛化误差 generalization error,注意不要和 期望 弄混了
泛化误差 generalization error 定义如下:
上式需要我们在了解 f(x) 和 p(x) 来求解,显然不可能。现实中,我们会构造一个 test set 或者 validation set 来近似 泛化误差 的评估。其实这也就是通过采样来近似估计期望:
接下来,最重要的一点是:使用不同的训练集 Dataset 我们会得到不同的模型参数 w ;所有模型整合到一块的 average response 就是 ED[f(x|w)] ,也就是 Figure 1. 中的绿点;由此引出 bias 和 variance 的精确描述:
- bias =Ex[(f(x)−ED[f(x|w)])2] ,反映了宏观上模型对 true function 的逼近能力
- variance =ED,x[(f(x|w)−ED[f(x|w)])2]=VAR[f(x|w)−ED[f(x|w)]] ,这就是所有模型对 average response(绿点)的方差;这直接反映的模型的稳定程度。overfitting 相关的 ill-conditioned problem 的结果就是模型对数据变化敏感;如果我们不同训练集得到的不同模型对于 unseen test data 的评判差异极大,那 variance 就会极大
bias 和 variance 在实践中无法精确估计,常见通过 cross-validation 的方法例如 k-fold 作近似计算。
最后,我们其实可以基于 泛化误差,直接分解为 bias-variance:
上述的 cross term 通过 ED 带入第一项后, ED[(f(x|w)−ED[f(x|w)]]=0 所以直接消除整项。
还有其他的 decomposition 解释方法,例如 wiki 上的版本为 true function f(x) 加入了一个 zero mean and variance σ2 的误差项 ϵ ,也就是说我们的观测本身就包含 unseen noise,这种 noise 是无法被消除的;所以其分解结果是:bias+variance+ σ2 ,本文不展开讨论。