数据科学家之路 实战1 --- O2O优惠券使用预测(part2)

 

本篇文章内容接着part1的模型部分

4.上模型

a.回归树

由于GBDT中用到的树是回归树，而不是我们一般用到的分类树，所以这里举个例子复习一下：

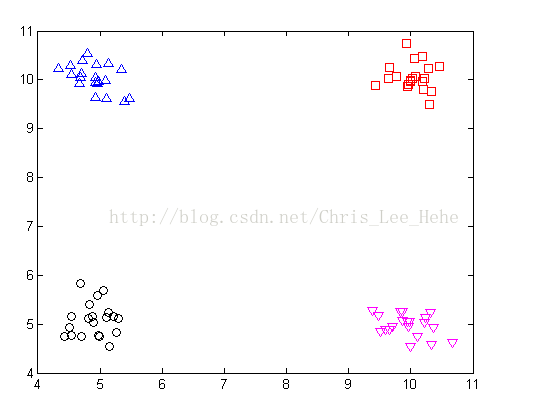
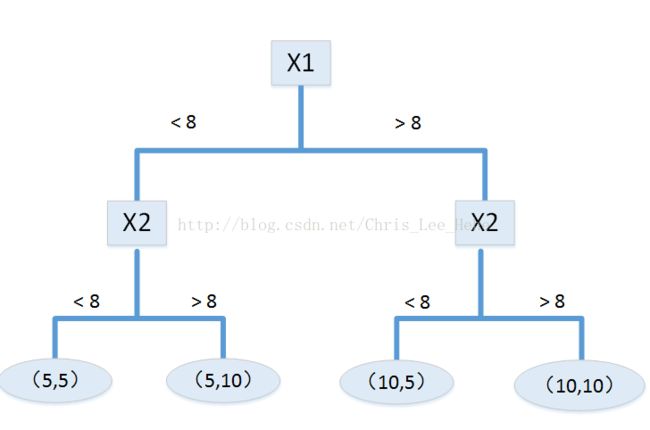
我们利用x1、x2这两个特征可以很容易地把数据分为四个区域，其中每个区域各有一个中心点（5,5）、（5,10）、（10,10）、（10,5），在对新数据做预测时，该数据落在哪个区域，就把该区域的中心点作为它的预测值。那么如何判断新数据将落在哪个区域呢？这时候“树”就派上用场了。我们可以这样建立一棵树：

这就是回归树的基本过程，那么接下来我们来看GBDT。

b.GBDT(Gradient Boosting Decision Tree) 梯度提升决策树

这里有必要先提几个重要的概念：

•   bootstrap：这个东西其实也是一个Web框架的名字，但是这里我们要说的是统计学中的一个方法。官方定义是:非参数统计中一种重要的估计统计量方差进而进行区间估计的统计方法。其实就是从大小为n的原始训练数据集D中随机选择n个样本点组成一个新的训练集，这个选择过程独立重复B次，然后用这B个数据集对模型统计量进行估计（如均值、方差等）。由于原始数据集的大小就是n，所以这B个新的训练集中不可避免的会存在重复的样本。
•   bagging： 这个方法是从大小为n的原始训练数据集D中随机选择n′ (n′
•   boosting： 这个方法依次训练k个子分类器，最终的分类结果由这些子分类器投票决定。首先从大小为n的原始训练数据集中随机选取n1个样本训练出第一个分类器，记为C1，然后构造第二个分类器C2的训练集D2，要求：D2中一半样本能被C1正确分类，而另一半样本被C1错分。接着继续构造第三个分类器C3的训练集D3，要求：C1、C2对D3中样本的分类结果不同。剩余的子分类器按照类似的思路进行训练。boosting构造新训练集的主要原则是使用最富信息的样本。
•   adaboost： adaboost是boosting方法的一种改进。adaboost为每个样本赋予一个权值，adaboost希望在下一轮训练时被上一个子分类器正确分类的样本权重和与被错误分类的样本权重和相等，从而下一个子分类器会和前一个子分类器有较大差别。上一个子分类器在这个数据集上正确率为50%。

是不是感觉这几个其实差不多？？下面说说他们的主要区别：

bootstrap方法和另外三个功能是不同的，他主要用于统计量的估计(均值，方差)，而bagging、boosting 和 adaboost方法则主要用于多个子分类器的组合。而adaboost是boosting的改进，所以有点难以分清的其实是bagging和boosting。这里推荐这篇写的很详细的文章给大家。简单来说，Bagging中的每棵树之间是独立的，而Boosting中后一棵树是建立在前一棵树的基础上的。该篇文章最后给出了三个公式：

Bagging + 决策树 = 随机森林
AdaBoost + 决策树 = 提升树
Gradient Boosting + 决策树 = GBDT

下面正式开始谈GBDT：
GBDT的核心在于：每一棵树学的是之前所有树结论和的残差（预测值和真实值的差值），比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学。这就是Gradient Boosting在GBDT中的意义。所以这里我们要尤其注意的是：GBDT是把所有树的结论累加起来做最终结论的，每棵树的结论并不是年龄本身，而是年龄的一个累加量。

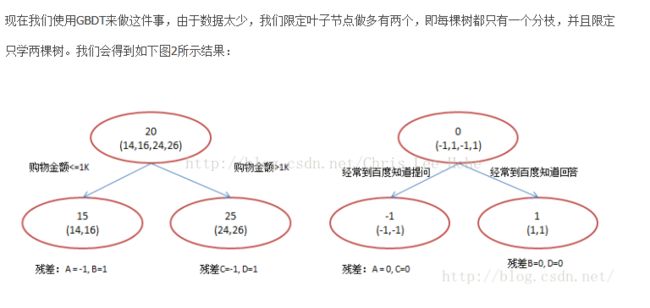
这里举个例子，来自这篇文章。

GBDT中，第一棵树分枝和一般回归树一样，由于A,B年龄较为相近，C,D年龄较为相近，他们被分为两拨，每拨用平均年龄作为预测值。此时计算残差，A的残差就是16-15=1（注意，A的预测值是指前面所有树累加的和，这里前面只有一棵树所以直接是15，如果还有树则需要都累加起来作为A的预测值）。进而得到A,B,C,D的残差分别为-1,1，-1,1。然后我们拿残差替代A,B,C,D的原值，到第二棵树去学习，如果我们的预测值和它们的残差相等，则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了。这里的数据显然是我可以做的，第二棵树只有两个值1和-1，直接分成两个节点。此时所有人的残差都是0，即每个人都得到了真实的预测值。

而体现了Gradient地方就是残差向量(-1, 1, -1, 1)，当我们用这个向量去二次优化时，也就是选择了下山的最快方向去下山！这就是Gradient的思想！

接下来我们看看在scikit-learn中简单的实现GBDT的代码：

 

import numpy as np
from sklearn.ensemble import GradientBoostingRegressor as GBR
from sklearn.datasets import make_regression
X, y = make_regression(1000, 2, noise=10)

gbr = GBR()
gbr.fit(X, y)
gbr_preds = gbr.predict(X)

这里再提几个GBR中较为重要的参数：

 

• n_estimators，就是GBR使用的学习算法（每个算法同时也是一棵树）的数量。通常，如果你内存够，可以把n_estimators设置的更大，效果也会更好。
• max_depth，这个参数应该在优化其他参数之前优化。因为每个学习算法都是一颗决策树，max_depth决定了树生成的节点数。选择合适的节点数量可以更好的拟合数据，而更多的节点数可能造成拟合过度。
• loss，它决定损失函数，也直接影响误差。ls是默认值，表示最小二乘法（least squares）。还有最小绝对值差值，Huber损失和分位数损失（quantiles）等等。

这里GBDT就说到这里，之后会再来补充这里。那么接下来就来看机器学习比赛大杀器：XgBoost

c.XgBoost（eXtreme Gradient Boosting）

 

to be continued...