HDU 1542 Atlantis（扫描线求矩形面积并+离散化）

http://acm.hdu.edu.cn/showproblem.php?pid=1542

题意就是给n个矩形，这些矩形可能存在覆盖的地方，求矩形面积并。这种题目要用到扫描线，同时还要用到离散化（一时因为数据特别大，二是因为题目中存在浮点数）。

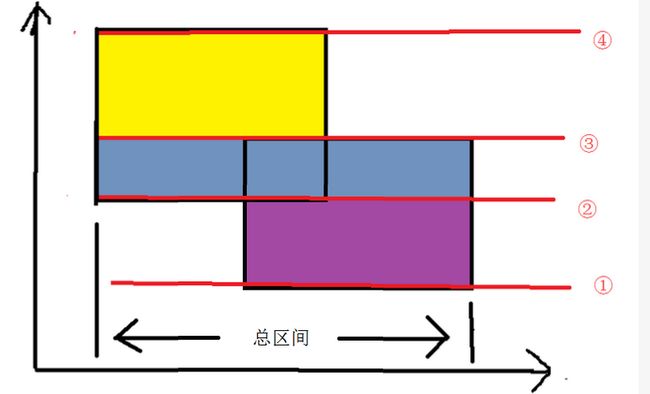
扫描线：一根虚拟的线，从下往上（或者从左往右）扫所求的图形，如下图所示，一条从下往上的直线扫到该4条线，并将图形分成三个部分分别来求面积。

扫描线解法（从下往上）：

• 将扫到的边加入到segment结构体中，这个结构体中是这样的：
  struct segment
  {
  double x1,x2,y;
  int flag;
  }arr[N];
  每个边存上左端点x1,右端点x2，以及该条线处于的y值。
  同时要是该条边是矩形的下边，那么将flag置为1，上边置为-1（具体为什么下面再说）

• 按照y值将结构体排序，从小到大的顺序

• 将扫描到的线依次插入到线段树中并求值

---

线段树在扫描线算法中的意义：线段树的总区间如上图所示是整个图形在x轴上的投影。当扫描到n条线段时，我们只需要插入n-1条线段。刚开始一条线段都没插入时，整个线段树的每个节点的值都为0，每插入一条线段，这时候线段树记录的就是当前覆盖的线段长度，每插入一条线段时，就可以将ans更新，ans+=tr[1]*(arr[i+1].y-arr[i].y);

怎样计算当前覆盖的长度：这时候flag的作用体现出来了，同时还要借助一个cover数组用于记录当前线段树该节点是否被覆盖过的情况。刚开始，要memset(cover,0),每插入一条线段的时候，cover数组更新成：cover[i]+=flag;上面说了将一个矩形的下底边的flag置为1，将上边置为-1，当插入下底边的时候,当前节点的cover[i]=1，当再插入上边的时候，cover[i]+=-1此时就变成了0，和初始状态一样，这样就完美的完成了删除操作。再根据cover[i]的情况push_up;

介绍下push_up的操作：
如果当前节点的cover[i]==1,就说明当前该点表示的线段被覆盖了，那么tr[i] = 实际长度。
否则的话，说明这个点表示的长度并没有完全被覆盖，如果这个点是叶子节点，那么tr[i]=0,如果不是叶子节点，tr[i]就由下面的左右子结点推来。

---

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

#define mset(x,y) memset(x,y,sizeof(x))
#define lson l,mid,i<<1
#define rson mid+1,r,i<<1|1
const int N = 200+10;
double has[N*2];//离散化数组
double tr[N*8];
int cover[N*8];

struct seg
{
    double x1,x2,y;
    int flag;
    friend bool operator < (const seg a,const seg b)
    {
        return a.y < b.y;
    }//将y值从小到大排序
}arr[N];
void pushup(int l,int r,int i)//very important！
{
    if(cover[i]) tr[i]= has[r+1]-has[l];
    else if(l==r) tr[i]=0;
    else tr[i]=tr[i<<1]+tr[i<<1|1];
    return;
}
void update(int l,int r,int i,int a,int b,int flag)
{
    if(l>=a&&r<=b)
    {
        cover[i]+=flag;
        pushup(l,r,i);
        return;
    }
    int mid=(l+r)>>1;
    if(mid>=a) update(lson,a,b,flag);
    if(midreturn;
}
int main()
{
    int n,cas=1;
    while(~scanf("%d",&n))
    {
        if(n==0) break;
        int t=0;
        for(int i=0;idouble x1,y1,x2,y2;
            scanf("%lf %lf %lf %lf",&x1,&y1,&x2,&y2);
            arr[t].x1=x1,arr[t].x2=x2,arr[t].y=y1,arr[t].flag=1; //扫描边
            has[t]=x1;
            t++;
            arr[t].x1=x1,arr[t].x2=x2,arr[t].y=y2,arr[t].flag=-1;
            has[t]=x2;
            t++;
        }
        sort(arr,arr+t);
        sort(has,has+t);//离散化操作
        double ans=0;
        mset(tr,0);mset(cover,0);
        for(int i=0;i1;i++)
        {
            int xx = lower_bound(has,has+t,arr[i].x1) - has ;
            int yy = lower_bound(has,has+t,arr[i].x2) - has - 1;
            if(xx<=yy) update(0,t-1,1,xx,yy,arr[i].flag);
            ans += tr[1]* (arr[i+1].y-arr[i].y);//更新ans
        }
        printf("Test case #%d\nTotal explored area: %.2lf\n\n",cas++,ans);
    }
    return 0;
}

关于push_up操作和cover数组要多理解 :)