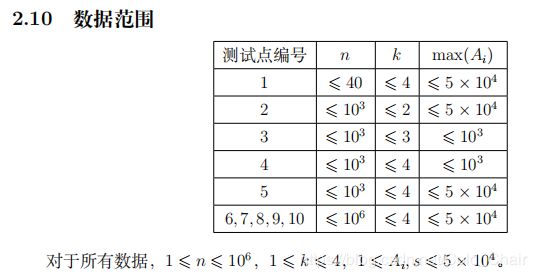
【WC2019模拟2019.1.14】选数

Description：

题解：

有gcd那先反演掉。
$\sum \sum gcd(a,b)$
$={\sum }_{d}d\ast [d|a]\ast [d|b]\ast [(a/d,b/d)=1]$
$={\sum }_{d}d\ast {\sum }_{d^{\prime }}\mu (d^{\prime })\ast {\sum }_{d{d}^{\prime }|a}{\sum }_{d{d}^{\prime }|b}I$
$={\sum }_d({\sum }_{d^{\prime }|d}\mu (d^{\prime })\ast (d/d^{\prime })){\sum }_{d|a}{\sum }_{d|b}$
$={\sum }_d\varphi (d)\ast {\sum }_{d|a}\ast {\sum }_{d|b}$

其实这个也可以由${\sum }_{d|n}\varphi (d)=n$直接得来。

那么问题变成了枚举d，然后把d的倍数弄出来，使异或和为s。

我们只考虑k=4的情况，显然更小的k更简单。

先不考虑重复，之后再来减。

可以设阈值M，当d<=M的时候，d的倍数比较多，可以用FWT暴力统计，当d>M的时候，d的倍数比较少，可以meet-in-middle。

第一部分复杂度为$O(M\ast n\ast logn)$，
第二部分复杂度为${\sum }_{i=M+1}^n(n/d{)}^2$

这个我不会化简，但是感受的到不会很大，随便平衡规划一下。

然后就是重复，注意s>0，所以只有两种情况：
1 3
1 1 2

那么只要枚举一个id,若s^(id)=j*d,算一下即可，系数也很好推。

Code：

#include
#include
#define pp printf
#define ll long long
#define fo(i, x, y) for(int i = x; i <= y; i ++)
#define ff(i, x, y) for(int i = x; i < y; i ++)
using namespace std;

const int mo = 998244353;

ll ksm(ll x, ll y) {
	ll s = 1;
	for(; y; y /= 2, x = x * x % mo)
		if(y & 1) s = s * x % mo;
	return s;
}

ll ni2;

const int N = 65536, M = 128;

int n, k, s, x;
int cnt[N];

ll a[N], b[N]; int tp, r[N];
void dft(ll *a, int tp, int F) {
	int n = 1 << tp;
	for(int h = 1; h < n; h *= 2)
		for(int j = 0; j < n; j += 2 * h) {
			ll A, *l = a + j, *r = a + j + h;
			ff(i, 0, h) {
				A = *r, *r = (*l - A + mo) % mo, *l = (*l + A) % mo;
				if(F == -1) *l = *l * ni2 % mo, *r = *r * ni2 % mo;
				l ++, r ++;
			}
		}
}
void fwt(ll *a, ll *b, int tp) {
	int n = 1 << tp;
	dft(a, tp, 1); dft(b, tp, 1);
	ff(i, 0, n)	a[i] = a[i] * b[i] % mo;
	dft(a, tp, -1);
}

int bz[N], p[N], phi[N], m;

void sieve(int n) {
	fo(i, 2, n) {
		if(!bz[i]) p[++ p[0]] = i, phi[i] = i - 1;
		for(int j = 1; i * p[j] <= n; j ++) {
			int k = i * p[j]; bz[k] = 1;
			if(i % p[j] == 0) {
				phi[k] = phi[i] * p[j];
				break;
			}
			phi[k] = phi[i] * phi[p[j]];
		}
	}
	phi[1] = 1;
}

ll ans, sum;
 
ll c2(ll n) {
	return n * (n - 1) / 2 % mo;
}

ll c3(ll n) {
	return n * (n - 1) * (n - 2) / 6 % mo;
}

ll pe[N], ni24;

int gcd(int x, int y) {
	return !y ? x : gcd(y, x % y);
}

ll g[N];
int c[1000005];

int main() {
	freopen("choose.in", "r", stdin);
	freopen("choose.out", "w", stdout);
	ni2 = ksm(2, mo - 2);
	ni24 = ksm(24, mo - 2);
	scanf("%d %d %d", &n, &k, &s);
	m = 65535; tp = 16;
	fo(i, 1, n) scanf("%d", &x), cnt[x] ++, c[i] = x;
	if(k == 1) {
		pp("%lld\n", (ll) cnt[s] * s % mo);
		return 0;
	}
	if(k == 2) {
		fo(i, 0, m) ans += (ll) cnt[i] * cnt[s ^ i] % mo * gcd(i, s ^ i) % mo;
		pp("%lld\n", ans % mo * ni2 % mo);
		return 0;
	}
	if(k == 3) {
		fo(i, 1, n) fo(j, i + 1, n) {
			int p = s ^ c[i] ^ c[j];
			if(p > 5e4) continue;
			if(cnt[p]) ans += gcd(c[i], gcd(c[j], p)) * cnt[p];
			if(p == c[i]) ans -= gcd(p, c[j]);
			if(p == c[j]) ans -= gcd(p, c[i]);
		}
		pp("%lld\n", ans / 3);
		return 0;
	}
	sieve(m);
	fo(d, 1, m) {
		sum = 0;
		if(d <= M) {
			ff(i, 0, 1 << tp) a[i] = b[i] = 0;
			fo(i, 1, m / d) a[i * d] = b[i * d] = cnt[i * d];
			fwt(a, b, tp);
			fo(i, 0, m) sum = (sum + a[i] * a[s ^ i]) % mo;
		} else {
			fo(i, 1, m / d) fo(j, 1, m / d)
				g[(i * d) ^ (j * d)] += (ll)cnt[i * d] * cnt[j * d] % mo;
			fo(i, 1, m / d) fo(j, 1, m / d)
				sum += g[s ^ (i * d) ^ (j * d)] % mo * cnt[i * d] % mo * cnt[j * d] % mo;
			fo(i, 1, m / d) fo(j, 1, m / d)
				g[(i * d) ^ (j * d)] -= (ll) cnt[i * d] * cnt[j * d] % mo;
		}
		int sp = 0; fo(i, 1, m / d) sp += cnt[d * i];
		fo(i, 1, m / d) {
			if((s ^ (i * d)) % d != 0) continue;
			int j = (s ^ (i * d)) / d; if(i > j) continue;
			if(!cnt[i * d] || !cnt[j * d]) continue;
			sum -= (ll) cnt[i * d] * cnt[j * d] % mo * 8 % mo;
			sum -= (ll) cnt[i * d] * cnt[j * d] % mo * (sp - 2) % mo * 12 % mo;
		}
		sum = (sum % mo + mo) % mo;
		ans = (ans + sum * phi[d]) % mo;
	}
	pp("%lld", ans * ni24 % mo);
}