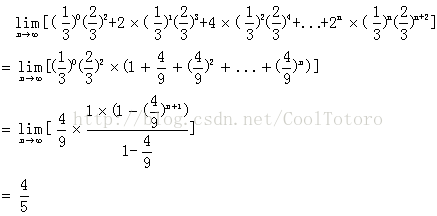网易大数据面试题试解
上周无意中看到了一份网易的面试题,说明为大数据部的面试题,粗略的看了一下,觉得挺有趣的,所以尝试着进行一下解答,首先要吐槽下,不知道这是什么级别岗位的题目,感觉有些不够专业,对大数据能力考察的题目几乎没有,大多是比较宽泛的问题,感觉各个岗位面试都可以问的那些问题。题目如下:
笔试:
1、甲和乙下棋,一局中甲获胜的概率为2/3,乙获胜的概率为1/3,一方比另一方多赢两局算赢,求甲获胜的概率?
答:条件比较少,切入点比较明确:一方比另一方多赢两局算赢,那么甲获胜的情况可以为
甲 2 乙 0
甲 3 乙 1
甲 4 乙 2
......
甲 n+2 乙 n
假设甲获胜情况为A概率记为p,乙获胜情况为B概率记为q,甲胜利的情况包括
AA 概率为 p^2
ABAA BAAA 概率为(2pq)*p^2
ABABAA ABBAAA BAABAA BABAAA 概率为(2pq)^2*p^2
以此类推
在笔试过程中,如果时间允许的话,可以再验证一下,乙胜甲的情况,通过同样的方法,得到乙获胜的概率为1/5,甲乙获胜概率相加为1,确认答案基本无误。
ps:一般笔试遇到此类问题,可以通过数学归纳法来做,很容易发现甲获胜的情况下,最后两次一定均为AA,为前面无论对局了多少轮,一定都是AB和BA的排列组合,找到规律的话就比较好做了。
2、有三个小球ABC,其中一个有奖,当你选择B球时,主持人跟你说C没有奖(假设主持人说的是真的),此时你有一次环球的机会,你会换球吗?
答:经典的“三门问题”,网上讨论的有很多,至今还有很多争论,简单列一下,不详细说了。
网上主要有3种观点:
1、换获益,因为B的1/3概率已确定,C的概率会转移到A上
2、无所谓,因为C的概率会平均转移.或者说B打开后条件变化,就不能已开始的条件计算概率
3、与主持人是否知情有关,知情则“换获益”,不知情则“无所谓”
其实说的都有道理,争论的原因在于这个问题最开始描述的时候,条件就有歧义。其实我们可以假设有一个不存在的另一个参赛者,选择了A门,第一轮来说,你和另一个参赛者分别选了A和B,那么你们两个人的获奖概率必然是相同的,都是1/3,当主持人打开C门后,你和另一个选择A门的参赛者获胜的概率依然相同,为1/2才对(否则你认为换门获胜概率高,对方也一样会认为换门的获胜概率高,双方就矛盾了)
那么问题到底出在什么地方呢?下面列个表格就明朗了,其实ABC三扇门的可能性只有如下几种(我们记两扇没有奖的门分别为N1、N2,有奖的门为Y)
A B C
1. N1 N2 Y
2. N1 Y N2
3. N2 N1 Y
4. N2 Y N1
5. Y N1 N2
6. Y N2 N1
我个人认为观点3很重要,即主持人是否知情很重要,这里列出的6中情况为主持人不知情的情况,这种情况下,无论如何你获奖的概率都是50%,肯定不变。现在假设主持人知情,对于1、2、3、4这四种情况,他一定会打开那扇没有奖的门(1、3打开B,2、4打开C),这4种情况下,剩下那扇门有奖的概率为100%,所以如果他命中了情况1、2、3、4,他换门的获奖概率升为100%,如果命中了5、6的情况下,换门的获奖概率为0,总体换门的获奖概率为66.7%
那我刚才提到的不存在的另一个参赛者的情况呢,这种情况下,假设你和另一个参赛者分别选取了N1和N2,另一扇门肯定是有奖的,这个时候,主持人无法打开第三扇门(因为主持人打开的那扇门是没有奖的,这种情况下打开第三扇门与题目不符),此时情况1、3是不存在的,在剩下的4种情况下,两位参赛者获奖的概率均为50%
3、f(f(x)) = -x,求f (其中x和f(x)都是整数)
答:这道题目前还没解出来,刚开始拿到这个题也没多想,迭代函数的题目,两层迭代后为一次函数,那么f(x)也为一次函数
令f(x)=kx,那么f(f(x))=k^2x=-x
所以k^2=-1,所以f(x)=ix
然后发现了这个条件:其中x和f(x)都是整数
显然这个答案中f(x)不为整数,经过多方尝试,依然没有找到合适的解,如果有解的话,我觉得可能会是分段函数吧,继续尝试ing......
ps:虽然还没有答案,不过有一些想法,在解决这些问题的时候,我觉得需要始终记住的是,这是一份笔试题,并不是数学考试,所以思考的过程不会太复杂,也不会特别数学化。我最开始尝试的方法是令f(x)=t,x=f^-1(t),通过反函数的特性,求导什么的算出来,后来觉得越算越复杂,我觉得笔试过程中不应该出现这么复杂的数学过程,否则要么是思路有问题,要么是选题有问题。
pps:感谢周某某大神帮助,解出了这个问题,不过从答案上来说很是奇葩,基本上是为了解题而强行构造一个函数答案如下:
在x为奇数时f(x)=x+(-1)^[(x-|x|)/2x]
在x为偶数且不为0时f(x)=-{x-(-1)^[(x-|x|)/2x]}
在x=0时,f(x)=0
没错,就是这么个奇葩的分段函数
思路是把整数们分组,a b -a -b是一组它们互相形成循环
形成 f(a)=b f(b)=-a f(-a)=-b f(-b)=a 的循环
4、一个线段分成三段,这三段能够拼成三角形的概率
答:线性规划问题,按照构成三角形的条件,计算条件概率即可
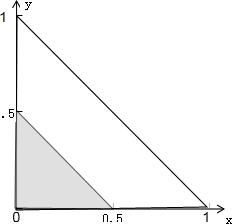
假设这三段线段总长度为1,分别长为x,y,1-x-y
那么总区域为0
三角形要求两边之和大于第三边,即
x+y>1−x−y ,x+1−x−y>y ,y+1−x−y>x
如图,大三角形面积为总区域,条件区域为阴影部分,显然概率为25%
5、一只股票的每日收盘价存在一个数组中,现在你选择一天买入,随后选择一天卖出,不考虑时间价值,设计算法求解可能得到的最高收益
答:Leetcode上的121题,策略比较简单
记录极小值low
遍历剩余的价格,假设当前价格为now,diff=now-low,如果diff<0,则最小值更新,若diff>max,则更新最大收益
遍历完数组之后,返回最大收益即可
转一段AC代码作为参考
class Solution {
public:
/**
* 计算最大收益
* @param prices : 每日价格
* @return : 最大收益
* @note : 只进行一次买卖
*/
int maxProfit(vector& prices) {
int pricesSize = prices.size();
/* 如果价格数据为空,或者只有一个数据,返回0 */
if (pricesSize <= 1) return 0;
int day, diff, min = prices[0], max = 0;
for (day = 1; day < pricesSize; ++day) {
diff = prices[day] - min;
if (diff < 0) min = prices[day];
else if (diff > max) max = diff;
}
return max;
}
}; 6、一道计算贝叶斯概率的题目
答:题目没有描述清楚,不过贝叶斯的题目就是熟记贝叶斯公式,从要求的值入手,尝试分解即可
面试:
面试部分大多是关于项目的问题,挑一些技术性问题简单分析一下吧
1、介绍SVM的原理
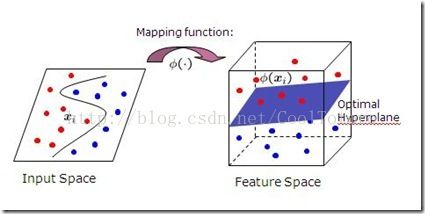
答:SVM是一种经典的分类器,中文名叫支持向量机,简单的来说,就是把你要分类的数据先向量化,一些在低维度线性不可分的数据到了高维度就线性可分了,如下图
当把数据映射到高维度后,直接线性划分即可分类,但是这里有个问题,就是随着维度的升高,比如原来是2维的可能到5维才能线性可分,3维的可能要到十几维才能线性可分,随着原始维度的升高,需要映射的维度也爆炸性升高,这时候我们就需要核函数来实现了,核函数的作用就是在低维度进行运算后再隐式映射到高维,这样一来线性可分的问题解决了,维度爆炸的问题也解决了,可以说是svm的核心
那么我们如何衡量svm的分类准确度呢,就是看这些点到超平面的距离,离得越远越好,这里我们有一个松弛变量的概念,某些噪声点超出了超平面,离群过远,这类点的引入对我们的分类算法影响较大,因为为了应付这些点,我们不得不再次挪动超平面,反而可能丢失了大部分点的分类精度,这时候我们设定一个阈值,没离群的点松弛变量为0,最终对离群点的权重做一定的惩罚,惩罚因子C体现了分类器对于离群点的重视程度。
仔细考虑一下,核函数和松弛变量实际上都是为了解决线性不可分的问题,那么为什么要用两种方法来实现呢,实际上,在引入核函数之前,大部分的点都是离群点,使用松弛变量带来的损失太大,所以先通过核函数,映射到接近线性可分的情况,只有少量的离群点,再通过松弛变量来剔除那些噪声点。
ps:网上一搜svm的原理一大堆,我不必说的过细,对于面试来讲,面试官既然问到了这个问题,证明他对这个问题比较熟,只是考察你有没有涉及过这类知识点,所以在面试的时候,大家对于一些基础的原理没必要说的太细,如果面试官有疑义,他会详细的提问,用比较简洁的话快速的介绍这项技术中最核心的原理,以及这个算法解决了什么样的问题,另外如果能用一两句话说出这个算法在同类算法中的优势和劣势,势必会有一个加分。通过一两句话把一个算法的精髓说出来,不拖泥带水才是熟练掌握这个算法的表现。
2、如何证明一个大于3的质数的平方减1可以被24整除
答:又是个数学问题,先给出简要一点的证明过程
假设这个数为p
首先对于(p-1)p(p+1),连续三个自然数必定有一个数能被3整除,且肯定不是p(否则p就不是质数了)
所以3 | (p+1)(p-1) (1)
其次p是质数,所以必然为奇数,那么
p≡1,3,5,7(mod 8),所以p^2≡1(mod 8)
所以8 | p^2-1 (2)
由(1)(2),所以24 | p^2-1
拿到这种题目,基本上一个条件就是一个解题的要点,一步一步分析就是了,首先看结论,被24整除,在我们的知识体系中,没有涉及过这么大的数的整除规律,则必然要分解,至少也要分解为3*8的形式,问题便化归为了证明既被3整除又被8整除
其次,大于3的质数,这些质数最大的(至少我第一时间能够想到的)就是这些数都是奇数,且都不能被3整除
大于3的质数的平方减1这个条件自然能转化为(p+1)(p-1)的形式,至此,这些条件都转化为了一个个的点,剩下的只是按照这些点进行组合得到结论就是了,能够把题目拆分成这些条件看的是基本功,能不能把这些条件整合出结论就是看能力了,好在面试并不会在数学上太过刁难大家,基本靠着以前的一些基本常识也能够拼凑出答案
ps:我始终认为太多的数学问题对于面试是无益的,除非是算法岗,那也应该紧扣算法来提问而不是考察,如果说上面笔试的线性规划和贝叶斯还是和算法沾边的话,这类数论的题目就不应该考察了,一定要靠到能力考核的话,我觉得唯一能考察的能力就是如何把问题分解为一系列更容易解决的问题,如何通过手里的一些基础知识来解决较难的问题。
3、给你五分钟,估计一下海淀区需要的共享单车数量
答:开放性问题,没有正确的答案,实际这类问题很多,这也是这次笔试面试中唯一和大数据关系比较近的题目,类似的大数据类问题很多,不过一般都是考察超大数据量下的算法设计,估算类题目较少,类似的问题可以参考编程珠玑第7章,估算方面的知识。这类题目从来不要求你求出一个具体的数字,也不可能,考察点在于你如何对问题进行分析,以及最重要的是,要“自圆其说”,至少在量纲上不能出大问题,剩下的就是仁者见仁智者见智了,你要展现出你回答问题的条理性,当然也要通过你的各种知识和常识进行辅助推算,如果你一开始就能够大概估计出一个量纲的话,剩下的就是如何让你的观点更加的靠近这个结论(共享单车几家公司,那么多大牛的工程师、高管啥的通力合作算出的每座城市的共享单车承载量,怎么可能你一个人5分钟的时间内就算出来呢,只能是尽可能的论证你的结论)
对于这个题目,我稍微说下我的想法:
1、考虑海淀区的人员组成:高新技术、高等学府、部分普通居民、还有一些流动人口聚集的地区
2、考虑平时骑共享单车的人的情况:高新技术和学校的学生是最可能骑车的,而普通居民和流动人口骑车的比例相对低一些
3、考虑骑车主要的用途:学生骑车出行,往返学校,上班族主要是上下班,地铁站周围人流密集
要素基本凑齐了,剩下就是根据海淀的人口数,大约3、400万,学校几十所,人数70w左右,高新技术公司员工总数估计也就100w,剩下的以普通居民居多,在这之中,学生对于共享单车的需求量是比较大的,公司员工也有需求,不过相对比例要小一些,前者使用率可达20%-30%,后者也就10%不到,普通居民使用率一般不高于2%,总的粗略一算大概需求量25w-30w量左右吧
ps:根据查到的资料,北京市今年预计摩拜和小黄车的投放总量可达到120w量,其中海淀区投放量30%左右,35w吧差不多,比我算法略微多一些,一般估算中算是可以接受的,不过我对于学生和职工的使用率估算过高了,可能某些类别的人群的数量估算还是差一些,总的来说这类题就是这么个思路,一定要让面试官看到你严谨的分析能力,只要结论不出大问题,注定会加分。
后记:这次对网易的笔试面试进行了一些简单的分析,抛砖引玉吧。笔试面试首先自然是要求大家掌握扎实的基础,对于岗位核心的能力肯定是要有的,至于各种题目都是万变不离其宗,面试的时候最容易紧张,其实很多时候放松下来,冷静的去分析各种条件,这些问题都不是特别的难。仔细想想,你要是面试官的话,你会如何提问,自然是有很多的考察点的对不对,现在作为去面试的一方,想一想对方问的这些问题最想看到的是你哪方面的能力,尽可能把你这方面的能力展示出来,自然就离成功不远了。面试最重要的是差异化,你会什么,你和别人有何不同,比如机器学习中的某些算法,各个公司都在做,你做的又有何不同呢,你的差异决定了你体现出的价值,这一点也是尤其能让面试官记住你的一点。