支持向量机的代码实现

前言：
本篇文章主要实现了《机器学习实战》的支持向量机部分，我在代码中也尽量描述了对应公式的哪些变量。我建议搭配《统计学习方法》进行实战，下面这篇博文对于公式推导也是很不错的。

https://blog.csdn.net/u011067360/article/details/26503719

另外本篇依赖于jupyter notebook。故在代码后面会出现相应的结果。

正文：

SMO算法求支持向量机

SMO算法中的辅助函数

def loadDataSet(fileName):
    """读取数据"""
    dataMat = [];labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]),float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat,labelMat

def selectJrand(i,m):
    """
    参数i：第一个alpha的下标，参数m：所有alpha的数目
    在某个区间范围随机取一个整数
    """
    j = i
    while(j == i ):
        j = int (random.uniform(0,m))
    return j

def clipAlpha(aj,H,L):
    """用于在数值太大时进行调整"""
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj

dataArr,labelArr = loadDataSet("E:\\DataMining\\Project\\MLBook\\机器学习实战源代码\\machinelearninginaction\\Ch06\\testSet.txt")

简化版SMO算法

def smoSimple(dataMatIn,classLabels,C,toler,maxIter):
    """参数dtatMatIn:数据集
       参数classLabels：类别标签
       参数C：常数C
       参数toler：容错率
       参数maxIter：退出前最大的循环次数"""
    dataMatrix = mat(dataMatIn);labelMat =mat(classLabels).transpose()
    b = 0;m,n = shape(dataMatrix)
    alphas = mat(zeros((m,1)))
    iter = 0  #储存在没有任何alpha改变的情况下遍历数据集的次数
    while(iter < maxIter):
        alphaPairsChanged  = 0  #记录alpha是否已优化
        for i in range(m):
            #multiply() 数组元素对应相乘
            #fXi 是预测值
            fXi = float(multiply(alphas,labelMat).T *\
                       (dataMatrix * dataMatrix[i,:].T)) + b
            Ei = fXi - float(labelMat[i])
            #违反KKT条件最严重
            # 以下几种情况出现将会出现不满足：（ui是预测值，ai是变量alpha）
            #yiui<=1但是ai
            #yiui>=1但是ai>0则是不满足的而原本ai=0   
            #yiui=1但是ai=0或者ai=C则表明不满足的，而原本应该是0
            #所以要找出不满足KKT的这些ai，并更新这些ai
            #在考虑这些点时有首先考虑0
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or \
                ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
                    #随机选择第二个alpha
                    j = selectJrand(i,m)
                    fXj = float(multiply(alphas,labelMat).T*\
                               (dataMatrix*dataMatrix[j,:].T)) + b 
                    Ej = fXj - float(labelMat[j])
                    alphaIold = alphas[i].copy();alphaJold = alphas[j].copy()
                    #对类别同号异号分开求上下界
                    if (labelMat[i] != labelMat[j]):
                        L = max(0,alphas[j] - alphas[i])
                        H = min (C,C + alphas[j] - alphas[i])
                    else:
                        L = max(0,alphas[j] + alphas[i] - C)
                        H = min(C,alphas[j] + alphas[i])
                    if L==H:
                        print('L==H')
                        continue
                    #最优修改量eta
                    eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T -\
                          dataMatrix[i,:]*dataMatrix[i,:].T -\
                          dataMatrix[j,:]*dataMatrix[j,:].T
                    if eta >= 0:
                        print('eta>=0')
                        continue
                    #之所以是-=  是因为前面eta的求法对比书上公式是相反数的
                    alphas[j] -= labelMat[j] * (Ei-Ej)/eta
                    alphas[j] = clipAlpha(alphas[j],H,L)  #调整alpha[j]
                    if (abs(alphas[j] - alphaJold) < 0.00001):
                        print('j not moving enough')
                        continue
                    #对i进行修改，修改量与j相同，方向相反
                    alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
                    #重新计算阈值b
                    b1 = b - Ei -labelMat[i]*(alphas[i]- alphaIold)* \
                        dataMatrix[i,:]*dataMatrix[i,:].T - \
                        labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                    b2 = b - Ej -labelMat[i]*(alphas[i]- alphaIold)* \
                        dataMatrix[i,:]*dataMatrix[j,:].T - \
                        labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
                    if (0 < alphas[i]) and (C > alphas[i]):
                        b = b1
                    elif (0 < alphas[j]) and (C > alphas[j]):
                        b = b2
                    else:
                        b = (b1 + b2 ) / 2.0
                    alphaPairsChanged += 1
                    print('iter:{0} i:{1} paris change {2}'.format(iter,i,alphaPairsChanged))
        if (alphaPairsChanged == 0):
            iter += 1
        else:
            iter = 0
        print('iteration numebr :{}'.format(iter))
    return b,alphas

from numpy import *
b,alphas = smoSimple(dataArr,labelArr,0.6,0.001,40)

L==H
L==H
iter:0 i:8 paris change 2
j not moving enough
j not moving enough
iteration numebr :39
j not moving enough
j not moving enough
iteration numebr :40

b

matrix([[-3.85138014]])

alphas[alphas>0]

matrix([[0.11792374, 0.243914  , 0.00461456, 0.35722318]])

了解哪些数据点是支持向量

for i in range(100):
    if alphas[i] > 0.0:
        print(dataArr[i],labelArr[i])  # 输出对应下标的样本点

[4.658191, 3.507396] -1.0
[3.457096, -0.082216] -1.0
[5.286862, -2.358286] 1.0
[6.080573, 0.418886] 1.0

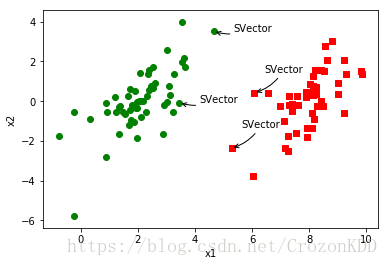
作图标记出来

def plotTool():
    import matplotlib.pyplot as plt
    dataMat,labelMat = loadDataSet("E:\\DataMining\\Project\\MLBook\\机器学习实战源代码\\machinelearninginaction\\Ch06\\testSet.txt")
    dataArr = array(dataMat)
    n = shape(dataArr)[0]
    xcord1 = [];ycord1 = []
    xcord2 = [];ycord2 = []
    for i in range(n):
        if int (labelMat[i]) ==1:
            xcord1.append(dataArr[i,0]);ycord1.append(dataArr[i,1])
        else:
            xcord2.append(dataArr[i,0]);ycord2.append(dataArr[i,1])     
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1,ycord1,c='red',marker='s')
    ax.scatter(xcord2,ycord2,c='green')
    plt.xlabel('x1');plt.ylabel('x2')
    #标记出支持向量
    ax.annotate("SVector",xy=(4.658191, 3.507396),xycoords='data',xytext=(20,0),textcoords='offset points',
               arrowprops=dict(arrowstyle='->',connectionstyle='arc3,rad=-0.2'))
    ax.annotate("SVector",xy=(3.457096, -0.082216),xycoords='data',xytext=(20,0),textcoords='offset points',
               arrowprops=dict(arrowstyle='->',connectionstyle='arc3,rad=-0.2'))
    ax.annotate("SVector",xy=(5.286862, -2.358286),xycoords='data',xytext=(10,20),textcoords='offset points',
               arrowprops=dict(arrowstyle='->',connectionstyle='arc3,rad=-0.2'))
    ax.annotate("SVector",xy=(6.080573, 0.418886),xycoords='data',xytext=(10,20),textcoords='offset points',
               arrowprops=dict(arrowstyle='->',connectionstyle='arc3,rad=-0.2'))                           
    plt.show()

plotTool()

计算w值

def calWs(alphas,dataArr,classLabels):
    X = mat(dataArr);labelMat = mat(classLabels).transpose()
    m,n = shape(X)
    w = zeros((n,1))
    for i in range(m):
        w += multiply(alphas[i]*labelMat[i],X[i,:].T)
    return w

w = calWs(alphas,dataArr,labelArr)

完整版Platt SMO的支持函数

PS:在calcEk()注释掉了后面引入核函数需要修改的部分

class optStruct:
    def __init__(self,dataMatIn,classLabels,C,toler):
        '''建立一个数据结构来保存所有重要的值'''
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]  #行
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0
        self.eCache = mat(zeros((self.m,2)))       #第一列给出的是eCache是否有效的标志位，第二列是实际的E值
def calcEk(oS,k):
    '''
    参数oS:optStruct的对象
    参数k:下标
    计算E值并返回'''
    #以下部分为未引入核函数后的fXk，Ek计算
    fXk = float(multiply(oS.alphas,oS.labelMat).T*\
               (oS.X*oS.X[k,:].T)) + oS.b
    #以下部分为引入核函数后的fXk，Ek计算
    #fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k]+oS.b)
    Ek = fXk - float(oS.labelMat[k])
    return Ek

def selectJ(i,oS,Ei):
    '''启发式方法选择内循环的alpha'''
    maxK = -1;maxDeltaE = 0;Ej = 0
    oS.eCache[i] = [1,Ei]
    #nonzero():
    #返回一个长度为a.ndim（数组a的轴数）的元祖，元祖的每个元素都是一个整数数组，其值为非零元素的下标在对应轴上的值
    #>>> b2 = np.array([[True, False, True], [True, False, False]])
    #>>> np.nonzero(b2)
    #(array([0, 0, 1], dtype=int64), array([0, 2, 0], dtype=int64))
    #它的第0个元素是数组a中值不为0的元素的第0轴的下标，第1个元素则是第1轴的下标，因此从下面的结果可知b2[0,0]、b[0,2]和b2[1,0]的值不为0：
    #matrix.A 表示将矩阵转为array数组
    validEcacheList = nonzero(oS.eCache[:,0].A)[0]
    if (len(validEcacheList)) > 1:
        #对E中非0的值的下标进行循环
        for k in validEcacheList:
            if k == i:
                continue
            Ek = calcEk(oS,k)
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE):
                maxK = k;maxDeltaE = deltaE;Ej = Ek
        return maxK,Ej
    else:
        j = selectJrand(i,oS.m)
        Ej = calcEk(oS,j)
        return j,Ej

def updateEk(oS,k):
    '''计算误差值并存入缓存中'''
    Ek = calcEk(oS,k)
    oS.eCache[k] = [1,Ek]

完整Platt SMO 算法中的优化例程

PS:下面代码内部增添了在引入核函数后的内容，会注释掉，要用时再删除注释即可

  File "", line 1
    PS:下面代码内部增添了在引入核函数后的内容，会注释掉，要用时再删除注释即可
                                         ^
SyntaxError: invalid character in identifier

def innerL(i,oS):
    Ei = calcEk(oS,i)
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or\
    ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
        j,Ej = selectJ(i,oS,Ei)
        alphaIold = oS.alphas[i].copy();alphaJold = oS.alphas[j].copy()
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0,oS.alphas[j]-oS.alphas[i])
            H = min(oS.C,oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0,oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C,oS.alphas[j] + oS.alphas[i])
        if L == H:
            print('L==H');return 0
        #下一行为未引入核函数后的：
        eta = 2.0 * oS.X[i,:]*oS.X[j,:].T - oS.X[i,:]*oS.X[i,:].T - oS.X[j,:]*oS.X[j,:].T
        #下一行为引入核函数后的：
        #eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j]
        if eta >= 0:
            print('eta>=0');return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
        updateEk(oS,j) #更新误差进缓存
        if (abs(oS.alphas[j] - alphaJold) < 0.00001):
            print('j not moving enough');return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
        updateEk(oS,i)
        #更新阈值b
        #以下b1，b2是未引入核函数之后的：
        b1 = oS.b - Ei -oS.labelMat[i]*(oS.alphas[i]-alphaIold)*\
            oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*\
            (oS.alphas[j] - alphaJold)*oS.X[i,:]*oS.X[j,:].T
        b2 = oS.b - Ej -oS.labelMat[i]*(oS.alphas[i]-alphaIold)*\
            oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*\
            (oS.alphas[j] - alphaJold)*oS.X[j,:]*oS.X[j,:].T
        #以下b1，b2是引入核函数之后的：
        #b1 = oS.b - Ei - oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] -\
        #    oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
        #b2 = oS.b - Ej - oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j] -\
        #    oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
            oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
            oS.b = b2
        else:
            oS.b = (b1 + b2)/2.0
        return 1
    else : return 0

完整版Platt SMO的外循环代码

def smoP(dataMatIn,classLabels,C,toler,maxIter,kTup=('lin',0)):
    oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler,kTup)
    iter = 0
    entireSet = True;alphaPairsChanged = 0
    while(iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        if entireSet:
            #遍历所有的值
            for i in range(oS.m):
                alphaPairsChanged += innerL(i,oS)
                print('fullSet,iter:{0} i:{1},pairs changed {2}'.format(iter,i,alphaPairsChanged))
            iter += 1
        else:
            nonBoundIs = nonzero((oS.alphas.A > 0)*(oS.alphas.A < C))[0]
            #遍历非边界值
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i,oS)
                print('non-bound,iter:{0} i:{1},pairs changed {2}'.format(iter,i,alphaPairsChanged))
            iter += 1
        if entireSet:
            entireSet = False
        elif (alphaPairsChanged == 0):
            entireSet = True
        print("iteration number:{}".format(iter))
    return oS.b,oS.alphas

进行测试

b,alphas = smoP(dataArr,labelArr,0.6,0.001,40)

fullSet,iter:0 i:0,pairs changed 1
fullSet,iter:3 i:96,pairs changed 0
fullSet,iter:3 i:97,pairs changed 0
fullSet,iter:3 i:98,pairs changed 0
fullSet,iter:3 i:99,pairs changed 0
iteration number:4

了解哪些数据点是支持向量,可以看到与简易版SMO是不一样的

for i in range(100):
    if alphas[i] > 0.0:
        print(dataArr[i],labelArr[i])  # 输出对应下标的样本点

[3.634009, 1.730537] -1.0
[3.125951, 0.293251] -1.0
[4.658191, 3.507396] -1.0
[3.223038, -0.552392] -1.0
[3.457096, -0.082216] -1.0
[5.286862, -2.358286] 1.0
[6.080573, 0.418886] 1.0

计算w值

ws = calWs(alphas,dataArr,labelArr)
ws

array([[ 0.74764704],
       [-0.17895243]])

以第一个数据点为例进行分类：大于0为正类，否则负类

dataMat = mat(dataArr)
dataMat[0]*mat(ws)+b

matrix([[-0.98996178]])

在复杂数据上应用核函数

核函数转换函数

def kernelTrans(X,A,kTup):
    '''
    返回一个指定类型的核函数
    参数kTup:是一个包含核函数信息的元组，第一个参数是描述核函数类型的字符串，其它2个参数是可能需要的可选参数
    '''
    m,n = shape(X)
    K = mat(zeros((m,1)))
    if kTup[0] == 'lin':
        K = X * A.T
    elif kTup[0] =='rbf':
        for j in range(m):
            deltaRow = X[j,:] - A
            K[j] = deltaRow*deltaRow.T
        K = exp(K/(-1*kTup[1]**2))
    else:
        raise NameError('Houston We Have a Problem - - That Kernel is not recognized')
    return K

class optStruct:
    def __init__(self,dataMatIn,classLabels,C,toler,kTup):
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]  #行
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0
        self.eCache = mat(zeros((self.m,2))) 
        self.K = mat(zeros((self.m,self.m)))
        #修改optStruct类，增加核函数
        for i in range(self.m):
            self.K[:,i] = kernelTrans(self.X,self.X[i,:],kTup)

利用核函数进行分类的径向基测试函数

def testRbf(k1=1.3):
    #训练部分
    dataArr,labelArr = loadDataSet('E:\\DataMining\\Project\\MLBook\\机器学习实战源代码\\machinelearninginaction\\Ch06\\testSetRBF.txt')
    b,alphas = smoP(dataArr,labelArr,200,0.0001,10000,('rbf',k1))
    dataMat = mat(dataArr);labelMat = mat(labelArr).transpose()
    svInd=nonzero(alphas.A>0)[0]
    sVs = dataMat[svInd]
    labelSV = labelMat[svInd]
    print("there are {} Support Vectors".format(shape(sVs)[0]))
    m,n = shape(dataMat)
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs,dataMat[i,:],('rbf',k1))
        predict = kernelEval.T*multiply(labelSV,alphas[svInd]) + b
        if sign(predict) != sign(labelArr[i]):
            errorCount += 1
    print('the training error rate is:{}'.format(float(errorCount)/m))
    #测试部分
    dataArr,labelArr = loadDataSet('E:\\DataMining\\Project\\MLBook\\机器学习实战源代码\\machinelearninginaction\\Ch06\\testSetRBF2.txt')
    errorCount = 0
    dataMat = mat(dataArr);labelMat = mat(labelArr).transpose()
    m,n = shape(dataMat)
    for i in range(m):
        kernelEval = kernelTrans(sVs,dataMat[i,:],('rbf',k1))
        predict = kernelEval.T*multiply(labelSV,alphas[svInd]) + b
        if sign(predict) != sign(labelArr[i]):
            errorCount += 1
    print('the test error rate is:{}'.format(float(errorCount)/m))

在测试前要将前面innerL()和calcEk()的注释掉未引入核函数的代码

testRbf()

fullSet,iter:0 i:0,pairs changed 1
fullSet,iter:5 i:97,pairs changed 0
fullSet,iter:5 i:98,pairs changed 0
fullSet,iter:5 i:99,pairs changed 0
iteration number:6
there are 27 Support Vectors
the training error rate is:0.01
the test error rate is:0.02