计算机图形学——透视&基透视

一.基础知识

1. 两个主要平面及其交线

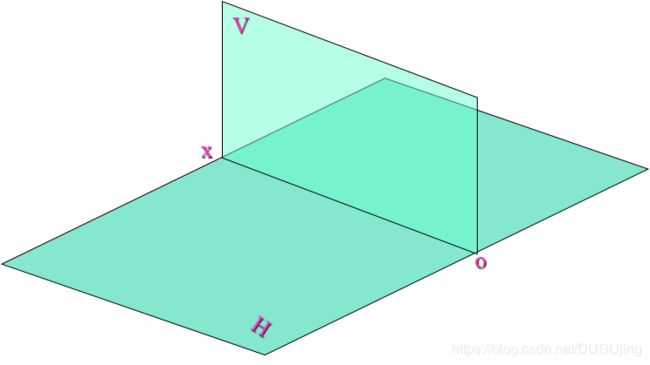
(1)画面(V)──透视所用的投影面，用符号V表示

(2)基面(H)──放置物体的水平面，相当于地面，用符号H表示。一般情况下，画面与基面相互垂直，所以可将它们看成是两投影面体系

(3) 基线(OX)──画面与基面的交线

 

图1-1
​​​

 

 2. 视点及其相关要素

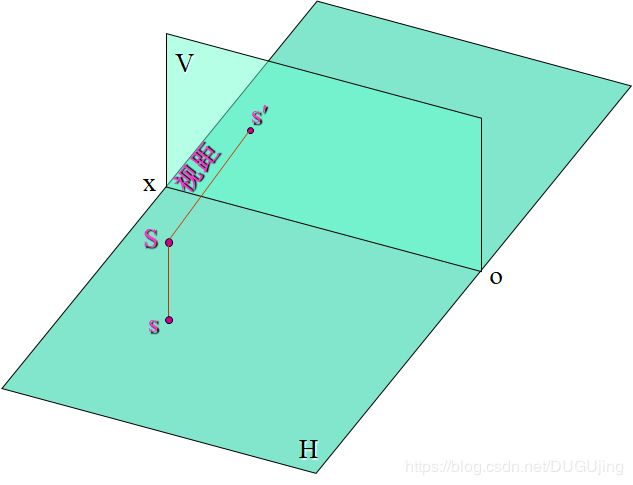
(1)视点(S)──投影中心（可想象为人的眼睛），用符号S表示

(2)站点(s)──视点在基面上的正投影，即人在观察形体时的立足点，用符号s表示

(3)主点(s′)──视点在画面上的正投影，用符号s′表示

(4)视距(Ss′)──视点到画面的距离

图1-2

(5)视高(Ss)——视点到基面的距离

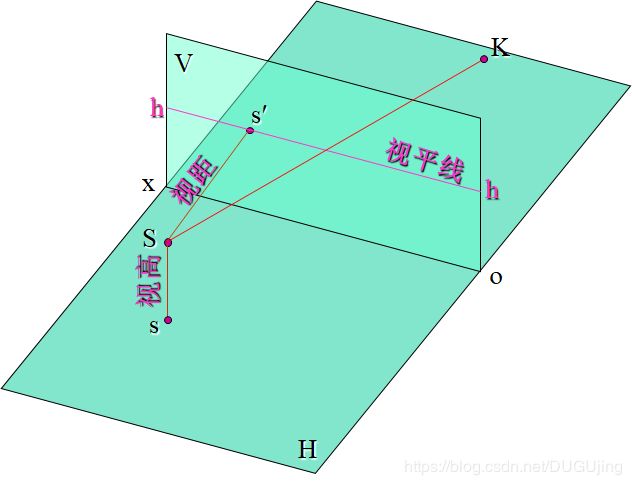
(6)视平线(h-h)——过视点与基面平行的平面与画面的交线，与基线平行，用符号h-h表示

（PS：视平线在画面(V)，是一条经过主点(s')，且平行于 OX(O'X') 的 线段）

(7)视线——即投射线，是视点与形体上的点的连线 

图1-3

 

二.点的透视

1. 点的透视特性

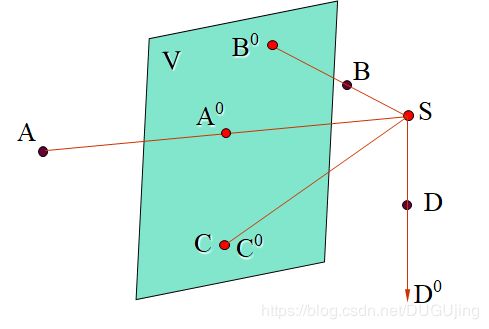
点的透视为通过该点的视线与画面的交点。一点在画面上，则其透视即为该点本身。

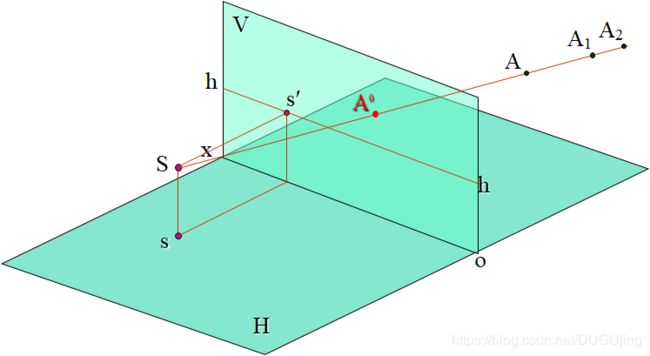
如图2-1，点A的透视就是过点A的视线SA与画面的交点，用符号A°表示。

图2-1

由图2-1可知，透视投影没有办法确定空间点与其透视投影间唯一的关系，所以在此，必须引入一个新的概念──基透视。

2. 点的基透视

如图2-2，空间点A的透视投影Ao 与它并非唯一对应，所有在视线SA上的点，如点A1、A2,……,它们的透视都是 A°。

图2-2

 

     空间点A在基面上的正投影a，称为点A的基点。a的透视就是A的基透视，用符号a°表示。

    过基透视a°作一视线Sa°，与基面只交于点a，而过a的铅垂线与过A°的视线SA°也只交于一点，即空间点A，可见，只要给定了A°和a°，在空间上就只有唯一的一点A与之对应。

 

图2-3

 

三. 点的（基）透视作图

1.空间点的透视，通常利用点的正投影作出（三维立体图 四条法则）

(1)点A的透视Ao  与其 基透视ao 在一天连线上，且垂直于基线

(2)垂足是视线SA 的 基面投影sa 与 基线的交点aox 

(3)点A的透视Ao  位于过该点的 视线SA 的 画面 正投影s′a′上

(4)点A的基透视ao 位于 视线Sa 的 画面 正投影s′ax上。

图3-1

 

为了方便作图，一般将画面与基面分离，并平放在同一平面上，基面与画面的边框不必画出（三维立体图变为平面图）

PS：基础知识

1.OX和O'X'其实是一条线，只是处于不同的平面，OX在 基面(H)，O'X'在 画面(V).

2.透视和基透视都在 画面(V)上

修改后的 四条法则 (平面图)： 

1.A点 的 透视Ao  与其 基透视ao 在一天连线上，且垂直于基线

2.垂足 是 站点 s 与 基点a 的连线 交 基线OX(O'X') 的 交点 aox

3.透视 在 主点 s' 与 被透视点(A) 在 画面上的 正投影(a') 的连线上 ；透视点 是 垂足 与 s'a' 的交点

4.垂足 在 主点 s' 与 被透视点(A) 的基点 (a) 在 画面上的 正投影(ax) 的连线上；基透视点 是 垂足 与  s'ax 的交点

PS：三位立体图 也 适用

 

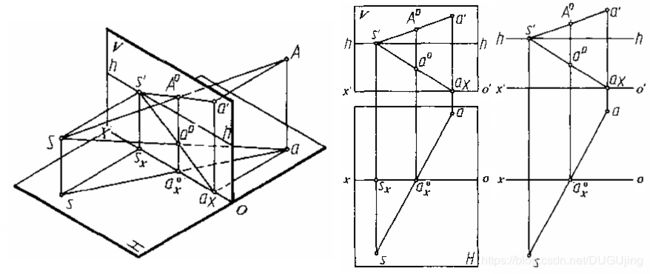图3-2

 2.示例一 点的透视

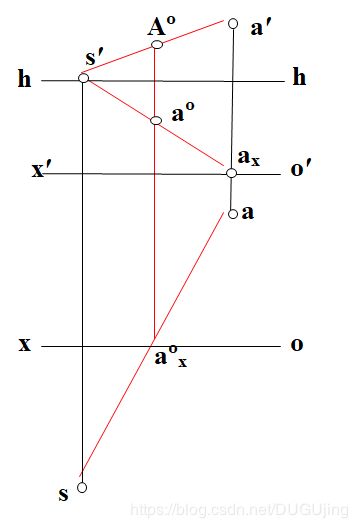图3-3

如图3-3所示，已知视点S和A点在基面和画面上的正投影，求作A点的透视和

基透视。

作图过程:

(1)连接sa交ox于aox

(2)连接s ′a＇

(3)连接s′ax

(4)过aox作直线垂直于o′x′, 交s′ax于ao，

交s′a＇于Ao，则A°为点A的透视，ao 为点A的基透视。

 

3.示例二 线的透视

如图3-4，AB∥V，已知视点S和直线AB的V面投影和H面投影，求作AB的透视（结果如图3-5）

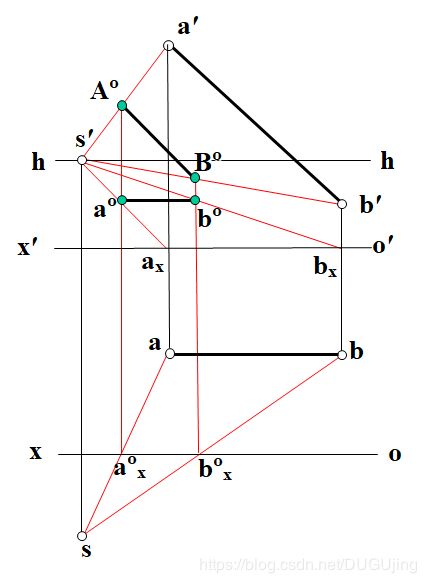图3-4 图3-5

作图过程:先基面(1,2),在画面(3,4,5,6,7)

(1) 连接sa交ox于aox

(2) 连接sb交ox于box

(3) 连接s ′a′

(4)连接s′b′；

(5)连接s′ax；

(6)连接s′bx；

(7)过aox作直线垂直于o′x′,交s′a′于A°，交s′ax于a°；过box作直线垂直于o′x′,交s′b′于B°，交s′bx于b°；则A°B°连线即为AB的透视，a°b°连线即为AB的基透视