机器学习入门及基本算法图解
基本算法
最近在学习神经网络,整理了一些算法,写出来给自己一点交代吧,本人刚入算法没多久,如果有不对的地方,请指出来大家一起学习,谢谢。
费曼算法(Feynman algorithm)
将这个算法放在最前面是因为该算法提供了一些我们思考问题的方法,根据吉德林法则:把问题清楚的写下来,就已经解决了一半!很多时候我们不知道怎么去解决问题,可以通过下面的三步来一步一步实施。这个算法是以著名物理学家理查德·费曼命名的,其步骤如下:
(1) 将问题写下来。
(2) 好好思考。
(3) 将答案写下来。
——Aditya Bhargava《算法图解》
算法简介
在百度百科上,算法是这么定义的:
算法(Algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。如果一个算法有缺陷,或不适合于某个问题,执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。
简单来说呢算法就是完成任务的指令,你可以把你曾经写过的代码想成要完成任务的指令,也就是算法,在这里介绍一些基本的算法以及示例,有很多人问我机器学习怎么入门,到底应该准备哪些基础知识。其实这个问题我也是头大,因为我是半路出家学习的算法,不过以前接触过一些算法方向的,比如做推荐系统时候的协同过滤算法,有兴趣的可以去看一下怎么实现的,本博客的KNN近邻算法里也有涉及到一些,对算法的思想入门还是有一点帮助的。emmmm 跑题了,咱们继续说机器学习需要具备的知识:
- 数学基础
- 典型机器学习算法
- 编程基础
很多盆友满怀激情来到了本博客,想要开始学习机器学习,但是在看到数学基础的那一刻就想放弃了,机器学习相对于其他开发工作来说,算的上门槛的也就是数学公式这一块了,每一个算法,要在训练集上最大程度拟合的同时又要保证泛化能力,就需要不断分析结果和数据,调优参数。这就需要我们对数据分布和模型底层的数学原理有一定的理解,所幸的是,如果只是想合理的应用机器学习,而不是做相关方向高精尖的research,需要的基础数学知识啃一啃还是基本能理解下来的,在这里有一句送给大家:“天下事以难而废者十之一,以惰而废者十之九”
微积分
微分的计算的意义及其几何、物理意义。是机器学习中大多数算法的求解过程的核心。比如算法中运用中的梯度下降法,牛顿法等。如果对几何意义有充分的理解的话,就可以理解为“梯度下降是用平面来逼近局部,而牛顿法是用曲面来逼近局部”,凸优化和条件最优化在算法里面随处可见,如果可以系统的学习的话会让你对算法的认识有一个新的高度。
线性代数
大多数机器学习的算法要应用起来,依赖于高效的计算,这种场景下,程序员GG们习惯的多层for循环通常就行不通了,而大多数的循环操作可转化成矩阵之间的乘法运算,这就和线性代数有莫大的关系了
向量的内积运算更是随处可见。矩阵乘法与分解在机器学习的主成分分析(PCA)和奇异值分解(SVD) 等部分呈现刷屏状地出现。
概率与统计
广义来说,机器学习在做的很多事情,和统计层面数据分析和发掘隐藏的模式,是非常类似的。
极大似然思想、贝叶斯模型 是理论基础,朴素贝叶斯(Na?ve Bayes )、语言模型(N-gram)、隐马尔科夫(HMM)、隐变量混合概率模型是他们的高级形态。
常见分布如高斯分布是混合高斯模型(GMM)等的基础。
图算法
在众多算法中,图算法算是比较经典的算法了,首先,我们说说什么是图
百度百科:图,汉语常用字,最早见于甲骨文 ,其本意原指古代在皮、绢等材料上标画城邦乡邑及边界的示意资料,后引伸为思虑、谋求、谋划,又引申为描画出来的形象化的作品、文件。
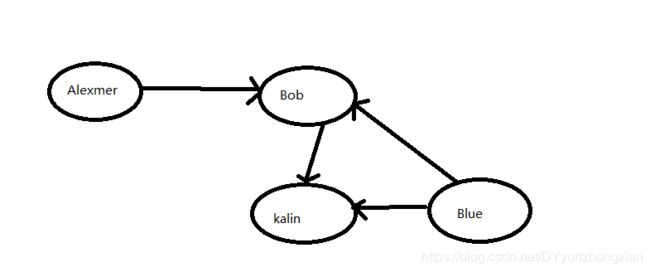
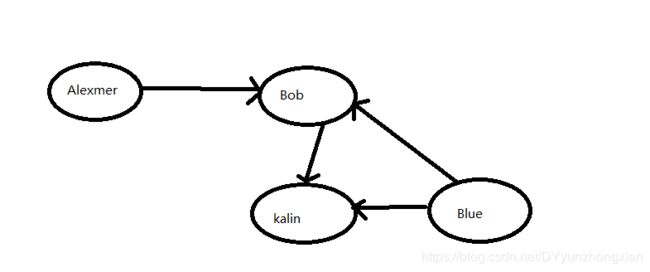
在算法中,图的意义大致上是模拟了一组连接关系。如下图,Alexmer是Bob的朋友,而Blue和kalin也是Bob的朋友。但是Alexmer和Blue并不认识。
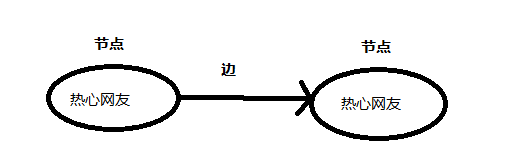
没错,图就是这个样子,图由节点和边组成,一个节点可能与很多其他节点相连,这些节点叫做该节点的邻居,如上图Alexmer,Blue,kalin 就是Bob的邻居。但Alexmer不是Blue的邻居,因为他们没有相连,图就是来模拟各个节点之间的关系的。
图的两种搜索方式
搜索是人工智能中的一种基本方法,是一项非常普遍使用的算法策略,能够解决许许多多的常见问题,在某些情况下我们很难想到高效的解法时,搜索往往是可选的唯一选择。按照标准的话来讲:搜索算法是利用计算机的高性能来有目的的穷举一个问题的部分或所有的可能情况,从而求出问题的解的一种方法。深度优先搜索与广度优先搜索都是用于图的查找算法,深度优先搜索用于早起的爬虫以及后来的搜索引擎算法,广度优先搜索常用于计算最短路径问题。
深度优先搜索(depth-first-search DFS)
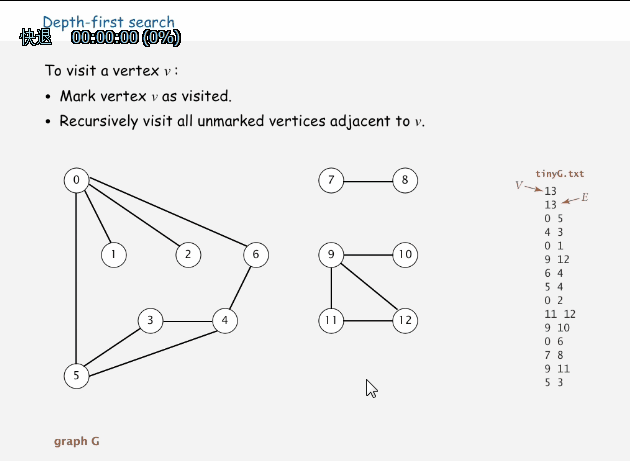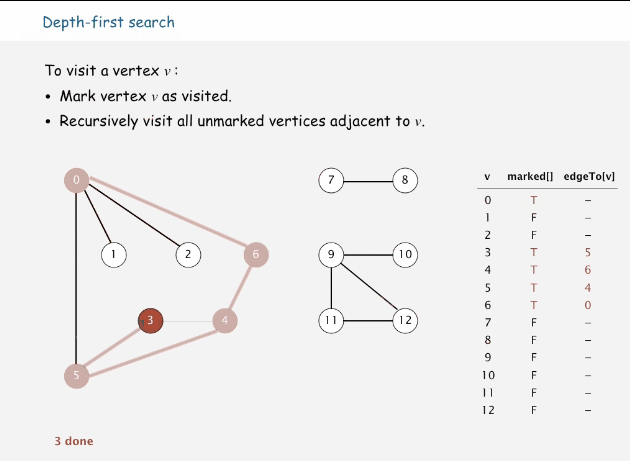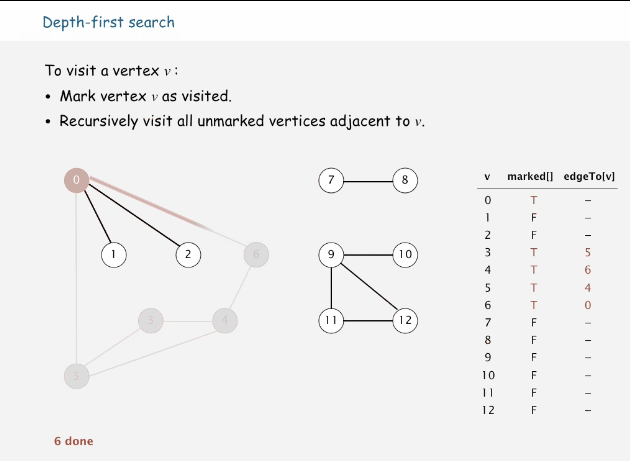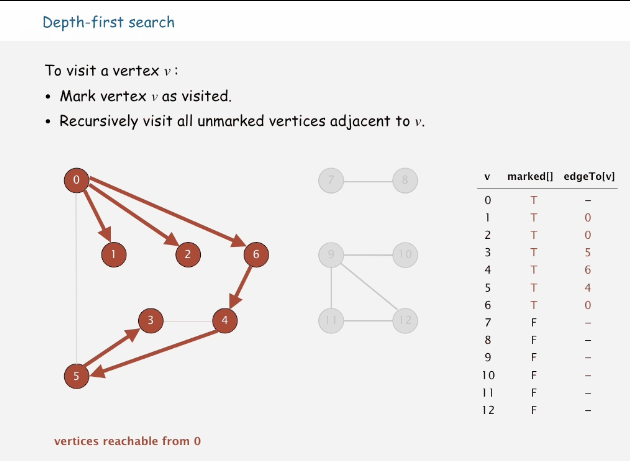
有很多人要问,为什么直接就来到了图的深度优先搜索,因为这个是我们要介绍的第一种图算法,其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。每当访问一个节点时,将其标记为已访问的节点,然后递归其相邻的节点,直到没有可以直接访问该节点的时候,就达到了该算法的目的。
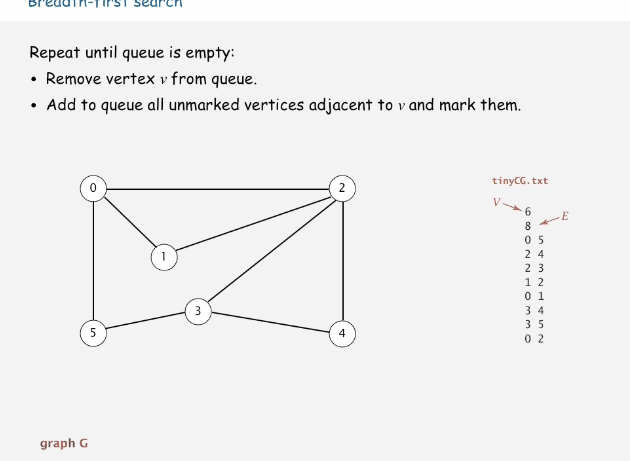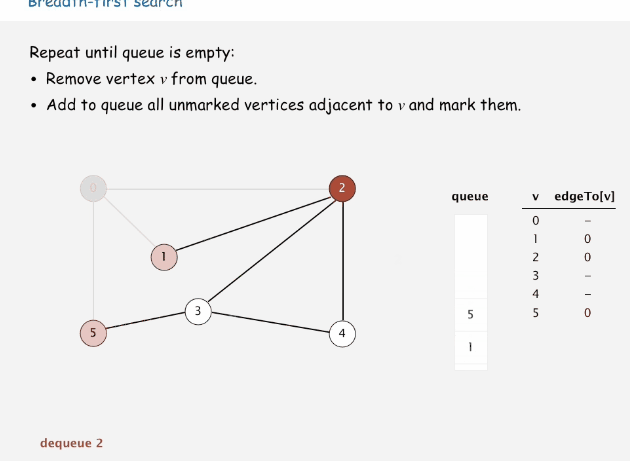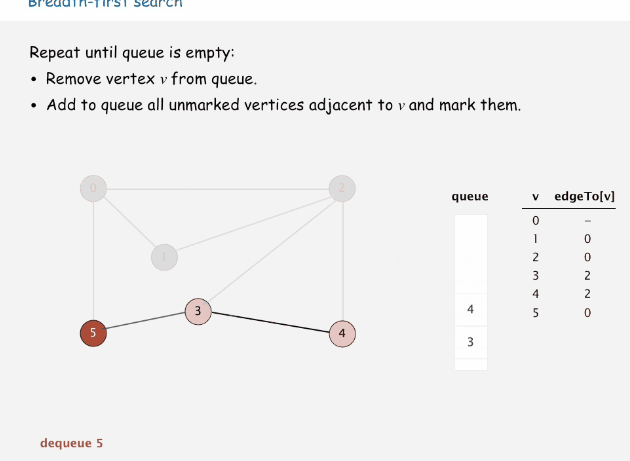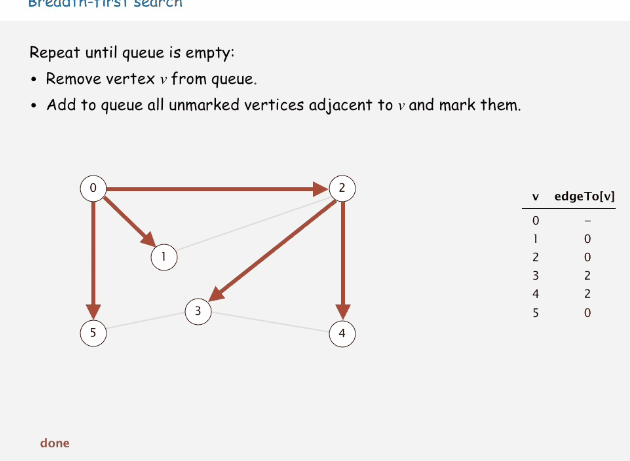
广度优先搜索(breadth-first search,BFS)
广度优先搜索又叫宽度优先搜索,是最简便的搜索图的算法之一,后续介绍的狄克斯特拉算法就是采用了宽度优先搜索类似的思想。属于一种盲目搜索法,他不会去考虑结果的位置,而是彻底搜索整张图,直到查到结果为止。

如上图所示,假设你居住在A地,想要去往F,那么就会延伸出两个问题:
- 从A出发,有前往F的路径吗
- 从A出发到F的最短路径是哪条
从A出发前往F,首先离你最近的两个点是B和C,你并不能一步走到F,所以首先来到了B和C,我们再接着走一步,很显然,两步也不能走到F,我们来到了B,D,Z,E,假设这四个节点对外突出,但是我们还是没有到达目标几点F,所以我们走出第三步,发现对外突出的节点D可以到达目标节点F,也就是我们所求的最短路径了。
散列表
不管如何,我们最终都要用代码来实现算法,图由多个节点构成,我们如何来表达各个节点构成的关系呢,它就是散列表。

散列表可以通过这种键值对的形式来将你的键映射到值。表示他的python代码如下:
graph={}
graph["Alexmer"]=["Bob"]
graph["Bob"]=["Blue"],["kalin"],["Alexmer"]
graph["kalin"]=["Bob"],["Blue"]
graph["Blue"]=["kalin"],["Blue"]
上面这种写法只是实现了散列表的一些基本结构,如访问该节点的判断还没写进去,真正开发的时候要考虑很多情况,这里只是做一个简单的参考。
迪杰斯特拉算法(Dijkstra)
迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。在我们用上面的广度优先搜索来求最短路径问题的时候,我们忽略了一个问题,就是时间,虽然从A-B-D-F是路径最短的,但是时间并不是最短的。

假设我们从A到B需要6分钟,但是从A到C只需要两分钟,再从C到B也需要两分钟,那么我们A-B>A-C-B,但是通过广度优先搜索的算法我们得到的路径确是A-B-D-F,这无疑会让你的路程多耗时两分钟(相对A-C-B-D-F而言),下面我们来看一下狄克斯特拉算法是怎么做的:

Dijkstra主要分为以下四个步骤:
- 找出在“最短时间”内可以到达的节点
- 更新一下所需要的“时间”,如上图从A到B记录为6,但是我们后来发现通过了C点到B比较“近”,就把“时间”更新为4
- 重复1,2步骤,更新每个到每个节点所需的“最短时间”
- 取目的节点的“最短时间”,计算完成
我们上文的“时间”其实就是权重,广度优先搜索所使用的不带权重的用来计算最短路径的图我们可以把它叫无权图,而狄克斯特拉算法所使用的带权重的图我们可以把它叫做有权图。其中,带有箭头指向的节点图我们可以把它叫有向图,而没有箭头指向的图我们可以把它叫做无向图,两个节点的无向图我们可以把它看做互相指向,构成了一个环形图,如下图所示:
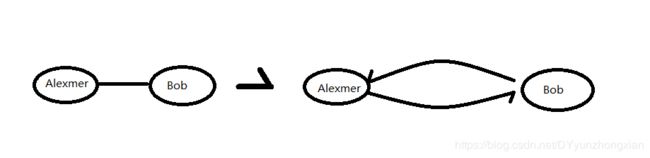
很显然,我们的狄克斯特拉算法并不适用于有环图,因为假设从别的节点流入A节点,那么每次绕环走都会增加权重,所得的路径不可能为最短路径,毕竟我们的狄克斯特拉要走完所有的路径,所以我们这里可以得出结论:狄克斯特拉算法只适用于有向无环图(directed acyclic graph,DAG)
贝尔曼福特算法(Bellman-Ford)
接下来,我们通过狄克斯特拉算法的一个例子来引出我们的贝尔曼福特算法:
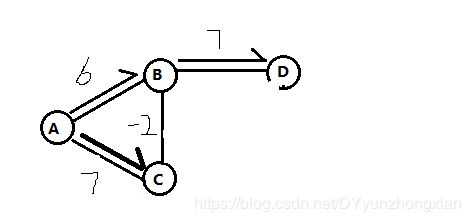
跟上面的图有所出入,这里我们按照狄克斯特拉的算法来求“最短路径问题”,可以看出我们从A-B
贝尔曼-福特算法(Bellman-Ford)是由理查德·贝尔曼(Richard Bellman) 和 莱斯特·福特 创立的,求解单源最短路径问题的一种算法。有时候这种算法也被称为 Moore-Bellman-Ford 算法,因为 Edward F. Moore 也为这个算法的发展做出了贡献。它的原理是对图进行V-1次松弛操作,得到所有可能的最短路径。
贝尔曼福特算法支持带有负权边的图,首先来说一下他的松弛操作,什么是松弛呢,看过很多文档,上面都没有详细的说明,都是直接进行的松弛操作,我的理解是松弛就是求所有节点和节点的“距离”,在我的印象中有点类似于笛卡尔积,比如上图的松弛操作为:求A-B,A-C,B-C,B-D的距离,计算完毕后再求A-C-B是否是否小于A-B,也就是最短路径,如果小于则更新最短路径,假设我们的图节点数量为V,边为E,那么我们的计算的时间复杂度为O(V*E),相比狄克斯特拉算法最大的好处就是贝尔曼福特算法可以进行松弛操作且支持负权边的计算。缺点则是时间复杂度过高。像狄克斯特拉算法优先选取没有被访问过的节点进行计算,实际上这种计算方法叫做贪婪算法。但是所得的结果并不全面。优点则是计算速度比较快。
计算机科学中,算法的时间复杂度是一个函数,它定性描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,它考察当输入值大小趋近无穷时的情况。
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
KNN近邻算法(k-Nearest Neighbor,KNN)
欢乐的时光总是短暂的,下面我们来看一下这最后一种基本算法,KNN近邻算法。
K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。该方法的思路是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
该算法通常用于做推荐算法。比如某电影APP,方块用户代表的是A类用户,不喜欢恐怖,也不喜欢惊悚的电影。五边形用户代表的是喜欢恐怖惊悚的用户,那么这时候来了一位新的用户A,根据A用户所观看的电影数据来看,距离方块用户比较近而且有两个方块邻居,距离五边形用户比较远,且邻居节点只有一个,那么你下次会向该用户推荐什么电影呢,很显然,会推荐一些不恐怖也不惊悚的,比如爱情片,文艺片。再通过爱情,文艺的KNN算法得出该用户最终喜欢的电影类型。这个问题就是机器学习中的分类问题,根据电影,用户的数据来对喜好进行分类。
这里要注意的是KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。KNN 算法本身简单有效,它是一种 lazy-learning 算法,分类器不需要使用训练集进行训练,训练时间复杂度为0。KNN 分类的计算复杂度和训练集中的文档数目成正比,也就是说,如果训练集中文档总数为 n,那么 KNN 的分类时间复杂度为O(n)。
其实在我们的生活中,有很多很多都离不开算法,比如早餐店,周一到周五会多准备一些食物,因为周一到周五上班的人比较多,但是比如周三下雨他就会准备的相对少一点,又比如周四是端午节,很多人放假,他就会少准备一些早餐(因为很多人不上班早上就不起床吃早餐),这些都是根据历史的经验来判断的,这里我们假设工作日为0,天气晴为0,没有节假日为0,那么我们周一卖的食物数量为A(0,0,0)=200,再假设周二是工作日,天气阴,不是节假日,我们周二卖出去的食物数量为B(0,1,0)=150,到了这里想必你们已经会记录每天的数据了,也可以根据“经验”来判断第二天需要准备的食物的数量了。这类问题在机器学习中叫做回归问题,也就是我们基于“经验”来做的预测问题。
余弦相似度
前面计算两位用户的距离时,使用的都是距离公式。还有更合适的公式吗?在实际工作中,经常使用 余弦相似度(cosine similarity)。假设有两位品味类似的用户,但其中一位打分时更保守。他们都很喜欢Manmohan Desai的电影Amar Akbar Anthony,但Paul给了5星,而Rowan只给4星。如果你使用距离公式,这两位用户可能不是邻居,虽然他们的品味非常接近。
余弦相似度不计算两个矢量的距离,而比较它们的角度,因此更适合处理前面所说的情况。
总结
将KNN近邻算法作为最后一个算法来讲解是因为这个算法真的很有用,其实大体上的算法都是算一下系数啊,权重啊,来让机器进行学习,因为计算机只懂得这种语言,我们通过经验来将数据转换为计算机的语言来让计算机进行学习,这里我们已经接触了机器学习的第一个例子:推荐系统,希望大家可以去多了解一下机器学习的知识,最后还是要强调一下机器学习的三个门槛:
- 数学基础
- 典型机器学习算法
- 编程基础
本文对这三个门槛都没有进行详细的讲解,因为这些知识都是需要大家不断的进行学习去累积,才能应用到真正的机器学习,而不是像作者一样只会“纸上谈兵”,哈哈,路漫漫其修远兮,吾将上下而求索。
参考文献
- 深度学习(DEEP LEARNING)
- 算法图解(Algorithmic Graphics)
- AI基础入门(AI Foundation)
- 百度百科(hhaha)