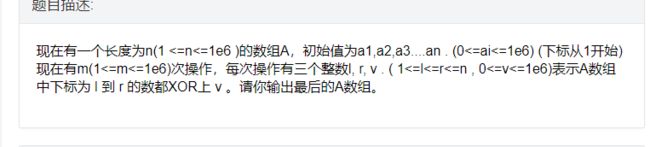
异或差分，前缀异或的概念

最近在做cometoj看题解的时候发现了异或差分这一性质。随性就在本校oj上出了个题，题是离线的，可以O（n）过，如果改成在线的可以用树状数组在O（n*logn） 。

问题链接：http://acm.nyist.cf/problem/1605

问题描述

与差分相似，我们构建一个异或差分数组B，那么B[i]=A[i]^A[i-1].，B[1]=A[1]。这样A[i]就可以B[i]的前缀异或得出。

这样有什么用呢？ 当我们将区间[l，r]全异或上v的时候，只有端点出B[l] 和B[r+1]改变了，我们只需将B[l]^=v,B[r+1]^=v即可

所以离线情况下直接O(m)就可以处理出m次操作后的结果

#include
#define mset(a,b) memset(a,b,sizeof(a))
typedef long long ll;
using namespace std;
const int N=1e6+10;
int A[N],C[N],L[N],R[N],V[N];
int main()
{
//    freopen("big_2.in","r",stdin);
//    freopen("big_2.out","w",stdout);
    int n,m;
    scanf("%d%d",&n,&m);
    A[0]=0;
    for(int i=1;i<=n;++i) scanf("%d",A+i);
    for(int i=1;i<=m;++i) scanf("%d%d%d",L+i,R+i,V+i);
    for(int i=1;i<=n;++i)
        C[i]=A[i-1]^A[i];
    for(int i=1;i<=m;++i)
    {
        int l=L[i],r=R[i],v=V[i];
        C[l]^=v;
        C[r+1]^=v;
    }
    int val=0;
    for(int i=1;i<=n;++i)
    {
        val^=C[i];
        printf("%d\n",val);
    }
    return 0;
}

 

如果是在线的怎么办？（q次操作，每次操作可能询问一个位置的值，或者将一个区间异或上v）

因为异或满足交换律，结合律，所以我们可以用树状数组维护的前缀异或。

但是复杂度是O(nlog(m)) ，因为本oj服务器较差，所以会超时，但是可以用超级快读优化

代码：（因为没有出在线修改和询问的题，所以这题先凑合用吧）

#include
#define mset(a,b) memset(a,b,sizeof(a))
typedef long long ll;
using namespace std;
const int N=1e6+10;
int A[N],C[N],L[N],R[N],V[N];
int bt[N],n,m;
namespace IO
{
    const int MX=4e7;
    char buf[MX];
    int c,sz;
    void begin()
    {
        c=0;
        sz=fread(buf,1,MX,stdin);
    }
    inline bool read(int &t)
    {
        while(c'9')) c++;
        if(c>=sz) return false;
        bool flag=0;
        if(buf[c] ==  '-')  flag=1,c++;
        for( t = 0; c0)
    {
        ans^=bt[k];
        k-=lowbit(k);
    }
    return ans;
}
int main()
{
//    freopen("big_2.in","r",stdin);
//    freopen("BB.out","w",stdout);
    IO::begin();
    IO::read(n);IO::read(m);
//    scanf("%d%d",&n,&m);
    A[0]=0;
    for(int i=1;i<=n;++i) IO::read(A[i]);
    for(int i=1;i<=m;++i)
    {
        IO::read(L[i]);
        IO::read(R[i]);
        IO::read(V[i]);
//      scanf("%d%d%d",L+i,R+i,V+i);
    }
    for(int i=1;i<=n;++i)
        modify(i,A[i-1]^A[i]);
    for(int i=1;i<=m;++i)
    {
        int l=L[i],r=R[i],v=V[i];
        modify(l,v);
        modify(r+1,v);
    }
    int val=0;
    for(int i=1;i<=n;++i)
    {
        printf("%d\n",getval(i));
    }
    return 0;
}

其实扩展的还可以有在线异或点，询问异或前缀和。以及差分乘法等概念（这名字我自己随便起的）

不过先到这里吧.