math: 交叉熵（Cross-Entropy）

0. 交叉熵（Cross-Entropy）

假设现在有一个样本集中两个概率分布p,q，其中p为真实分布，q为非真实分布。假如，按照真实分布p来衡量识别一个样本所需要的编码长度的期望为：
$$H(p)=\sum _{i}p(i)\cdot \log (\frac{1}{p(i)})$$
但是，如果采用错误的分布q来表示来自真实分布p的平均编码长度，则应该是：
$$H(p,q)=\sum _{i}p(i)\cdot \log (\frac{1}{q(i)})$$
交叉熵是一个在ML领域经常会被提到的名词。主要用于度量两个概率分布间的差异性信息,其可在神经网络(机器学习)中作为损失函数，$p$ 表示真实标记的分布，$q$ 则为训练后的模型的预测标记分布，交叉熵损失函数可以衡量 $p$ 与 $q$ 的相似性。交叉熵作为损失函数还有一个好处是使用 $sigmoid$ 函数在梯度下降时能避免均方误差损失函数学习速率降低的问题，因为学习速率可以被输出的误差所控制.

关于熵的一些物理意义可以解释为：

• 熵：事件A的信息量， 即A发生之后能够包含多少有用的信息。
• 相对熵（KL散度）：从事件A的角度上看，事件B有多大不同。
• 交叉熵：如何从事件A的角度来描述事件B。

1. 信息量

假设$X$是一个离散型随机变量，其取值集合为$X$，概率分布函数为 $p(x)=Pr(X=x),x\in X$
，我们定义事件 $X=x0$ 的信息量为： $I(x0)=-log(p(x0))$，可以理解为，一个事件发生的概率越大，则它所携带的信息量就越小，而当 $p(x0)=1$ 时，熵将等于0，也就是说该事件的发生不会导致任何信息量的增加。举个例子，小明平时不爱学习，考试经常不及格，而小王是个勤奋学习的好学生，经常得满分，所以我们可以做如下假设：

事件A：小明考试及格，对应的概率$P(x_A)=0.1$，信息量为:
$$I(x_A)=-log(0.1)=3.3219$$

事件B：小王考试及格，对应的概率$P(x_B)=0.999$，信息量为$$I(x_B)=-log(0.999)=0.0014$$

可以看出，结果非常符合直观：小明及格的可能性很低(十次考试只有一次及格)，因此如果某次考试及格了（大家都会说：XXX竟然及格了！），必然会引入较大的信息量，对应的I
值也较高。而对于小王而言，考试及格是大概率事件，在事件B发生前，大家普遍认为事件B的发生几乎是确定的，因此当某次考试小王及格这个事件发生时并不会引入太多的信息量，相应的$I$值也非常的低。

2. 熵定义

那么什么又是熵呢？还是通过上边的例子来说明，假设小明的考试结果是一个0 ~ 1分布$X_A$只有两个取值{0：不及格，1：及格}，在某次考试结果公布前，小明的考试结果有多大的不确定度呢？你肯定会说：十有八九不及格！因为根据先验知识，小明及格的概率仅有0.1,90%的可能都是不及格的。怎么来度量这个不确定度？求期望！不错，我们对所有可能结果带来的额外信息量求取均值（期望），其结果不就能够衡量出小明考试成绩的不确定度了吗。
即：

$$H_A(x)=-[p(x_A)\cdot log(p(x_A))+(1-p(x_A))\cdot log(1-p(x_A))]=0.4690$$

对应小王的熵：

$$H_B(x)=-[p(x_B)\cdot log(p(x_B))+(1-p(x_B))\cdot log(1-p(x_B))]=0.0114$$

虽然小明考试结果的不确定性较低，毕竟十次有9次都不及格，但是也比不上小王（1000次考试只有一次才可能不及格，结果相当的确定）

我们再假设一个成绩相对普通的学生小东，他及格的概率是$P(x_C)=0.5$ ,即及格与否的概率是一样的，对应的熵：

$$H_C(x)=-[p(x_C)\cdot log(p(x_C))+(1-p(x_C))\cdot log(1-p(x_C))]=1$$

其熵为1，他的不确定性比前边两位同学要高很多，在成绩公布之前，很难准确猜测出他的考试结果。

可以看出，熵其实是信息量的期望值，它是一个随机变量的确定性的度量。熵越大，变量的取值越不确定，反之就越确定。

对于一个随机变量X而言，它的所有可能取值的信息量的期望$（E[I(x)]）$就称为熵。

$X$的熵定义为：

$$H(X)=E_p\cdot log(\frac{1}{p(x)})=-\sum _{x\in X}p(x)\cdot log(p(x))$$

如果$p(x)$是连续型随机变量的$pdf$，则熵定义为：

$$H(X)=-{\int }_{x\in X}p(x)\cdot log(p(x))dx$$

为了保证有效性，这里约定当$p(x)\to 0$时,有$p(x)\cdot log(p(x))\to 0$

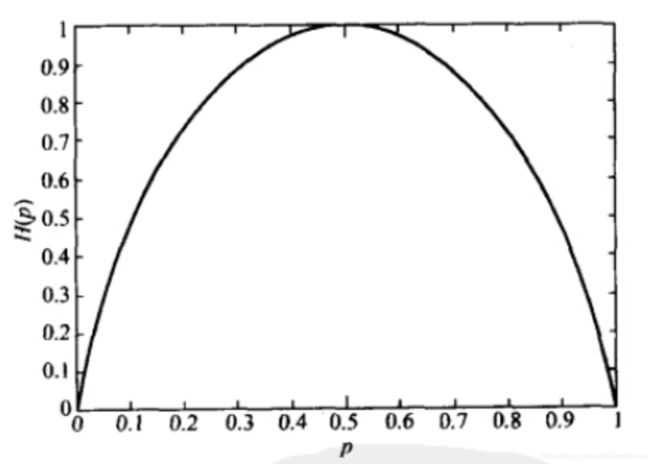
当$X$为0-1分布时，熵与概率p的关系如下图：

可以看出，当两种取值的可能性相等时，不确定度最大（此时没有任何先验知识），这个结论可以推广到多种取值的情况。在图中也可以看出，当$p=0$ 或 $p=1$时，熵为0，即此时$X$完全确定。

熵的单位随着公式中$log$运算的底数而变化，当底数为2时，单位为“比特”(bit)，底数为e时，单位为“奈特”。

3.相对熵

相对熵(relative entropy)又称为KL散度（Kullback-Leibler divergence），KL距离，是两个随机分布间距离的度量。记为$D_{KL}(p||q)$。它度量当真实分布为p时，假设分布q的无效性。
$$D_{KL}(p||q)=E_p\cdot [log(\frac{p(x)}{q(x)})]$$

$$=\sum _{x\in X}p(x)\cdot log(\frac{p(x)}{q(x)})$$

$$=\sum _{x\in X}[p(x)\cdot log(p(x))-p(x)\cdot log(q(x))]$$

$$=\sum _{x\in X}p(x)\cdot log(p(x))-\sum _{x\in X}p(x)\cdot log(q(x))$$

$$=-H(p)-\sum _{x\in X}p(x)\cdot log(q(x))$$

$$=-H(p)+E_p\cdot [-logq(x)]$$

$$=H_p(q)-H(p)$$

并且为了保证连续性，做如下约定：

$0\cdot log(\frac{0}{0})=0$，$0\cdot log(\frac{0}{q})=0$，$p\cdot log(\frac{p}{0})=\infty$

显然，当$p=q$时,两者之间的相对熵 $D_{KL}(p||q)=0$ 上式最后的 $H_p(q)$ 表示在 $p$ 分布下，使用 $q$ 进行编码需要的 $bit$ 数，而 $H(p)$ 表示对真实分布 $p$ 所需要的最小编码 $bit$ 数。基于此，相对熵的意义就很明确了：$D_{KL}(p||q)$ 表示在真实分布为 $p$ 的前提下，使用 $q$ 分布进行编码相对于使用真实分布 $p$ 进行编码（即最优编码）所多出来的 $bit$ 数。

参考：
https://blog.csdn.net/rtygbwwwerr/article/details/50778098
https://www.zhihu.com/question/65288314
https://baike.baidu.com/item/交叉熵