自编码器AutoEncoder(二)
那么既然编码器可以将784维的数据压缩到128维,把原数据的精髓提取到128维的空间中,而且自编码有点类似于PCA的做法,那么既然可以压缩,我把它压缩到二维或者三维空间可视化一下可不可以呢?答案是可以的。当把数据不断地压缩,然后解码,然后跟原始数据对比求出残差再反向传递,逐步减小损失的过程中,自编码器学到的东西会越来越好,压缩的精髓也就越来越能代表原始数据的分布,那么我就把原始数据压缩到2维或者3维,然后将特征分别代表x,y轴然后作图,看看0-9这110个数字是怎么分布的吧。下面是实现代码。
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('/tmp/data/',one_hot=False)
learning_rate = 0.001 #学习率,与之前不同的是这个学习率比上个更小
training_ephches = 50 #因为我压缩的维度只有两维,我需要更多的迭代次数,确保学习效果
batch_size = 256 #批数据量
display_step = 1
n_input = 784 #原始数据28*28
n_hidden_1 = 128 #第一层压缩到128维
n_hidden_2 = 64 #第二层压缩到64维
n_hidden_3 = 10 #第三层压缩到10维
n_hidden_4 = 2 #第四层压缩到2维
X = tf.placeholder(dtype="float32", shape=[None, n_input])
weights = {
'encoder_h1': tf.Variable(tf.random_normal([n_input , n_hidden_1])),
'encoder_h2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2])),
'encoder_h3': tf.Variable(tf.random_normal([n_hidden_2, n_hidden_3])),
'encoder_h4': tf.Variable(tf.random_normal([n_hidden_3, n_hidden_4])),
'decoder_h1': tf.Variable(tf.random_normal([n_hidden_4, n_hidden_3])),
'decoder_h2': tf.Variable(tf.random_normal([n_hidden_3, n_hidden_2])),
'decoder_h3': tf.Variable(tf.random_normal([n_hidden_2, n_hidden_1])),
'decoder_h4': tf.Variable(tf.random_normal([n_hidden_1, n_input])),
}
biases = {
'encoder_h1': tf.Variable(tf.random_normal([n_hidden_1])),
'encoder_h2': tf.Variable(tf.random_normal([n_hidden_2])),
'encoder_h3': tf.Variable(tf.random_normal([n_hidden_3])),
'encoder_h4': tf.Variable(tf.random_normal([n_hidden_4])),
'decoder_h1': tf.Variable(tf.random_normal([n_hidden_3])),
'decoder_h2': tf.Variable(tf.random_normal([n_hidden_2])),
'decoder_h3': tf.Variable(tf.random_normal([n_hidden_1])),
'decoder_h4': tf.Variable(tf.random_normal([n_input])),
}
#定义编码器
def encoder(x):
layer_1 = tf.nn.sigmoid(tf.add(tf.matmul( x , weights['encoder_h1']), biases['encoder_h1']))
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['encoder_h2']), biases['encoder_h2']))
layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, weights['encoder_h3']), biases['encoder_h3']))
layer_4 = tf.add(tf.matmul(layer_3, weights['encoder_h4']), biases['encoder_h4'])
return layer_4
#定义解码器
def decoder(x):
layer_1 = tf.nn.sigmoid(tf.add(tf.matmul( x , weights['decoder_h1']), biases['decoder_h1']))
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['decoder_h2']), biases['decoder_h2']))
layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, weights['decoder_h3']), biases['decoder_h3']))
layer_4 = tf.nn.sigmoid(tf.add(tf.matmul(layer_3, weights['decoder_h4']), biases['decoder_h4']))
return layer_4
encoder_op = encoder(X)
decoder_op = decoder(encoder_op)
y_pre = decoder_op
y_true = X
#定义损失函数和优化器
cost = tf.reduce_mean(tf.square(y_pre-y_true))
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)
#下面基本跟之前的类似
with tf.Session() as sess:
sess.run(tf.initialize_all_variables())
total_batch = int(mnist.train.num_examples/batch_size)
for epoch in range(training_ephches):
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.images[batch_size * i: batch_size * (i + 1)], \
mnist.train.labels[batch_size * i: batch_size * (i + 1)]
sess.run(optimizer, feed_dict={X: batch_xs})
if epoch % display_step == 0:
print('Epoch:{:2} ,cost={:.4f}'.format(epoch + 1,
sess.run(cost, feed_dict={X: batch_xs})))
print("Optimization Finished!")
#之前是从编码到解码,然后生成出的图片进行展示,这篇文章的目的是要对数据的分布进行一个可视化,那么
#我只需要把编码成2维的精髓拿出来,然后作为x,y轴,然后以点的方式分散在图上,这样就可以看出0-9这10个数字的分布
encoder_result = sess.run(encoder_op, feed_dict={X: mnist.test.images})
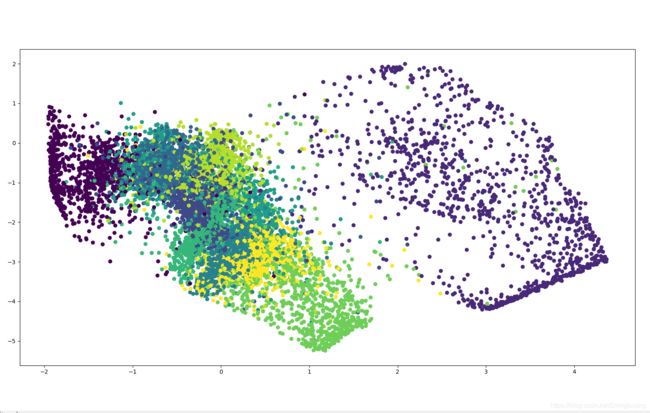
plt.scatter(encoder_result[:, 0], encoder_result[:, 1], c=mnist.test.labels)
plt.show()
下面代码运行结果,大致可以看出10个数字分别被区分到了不同的区域。
最后附上一段简化版的计算过程,可以帮助理解。在代码计算的过程中,shape往往是很重要的一个东西。如果不清楚某一段的shape是什么,可以选择打印。
'''这些代码只是帮助我印证一下这个shape到底是怎么变化的,尤其是biases加上去的时候,对这个这些数字到底是怎么变化的有一个直观的展示'''
import numpy as np
n_input=np.random.normal(size=[2,3]) #这个2相当于代码中的batch_size,3相当于代码中的28*28
weights = np.random.normal(size=[3,4]) #那么输入[2,3],权重[3,4],相乘之后shape=[2,4]
biases = np.random.normal(size=[4]) #直接打印biases的shape的时候,显示[4,]
n_input_weights=np.matmul(n_input,weights)
output = np.add(n_input_weights,biases)#在这里其实就用到了一种叫做广播的机制,将biases加到n_input_weights的每一行
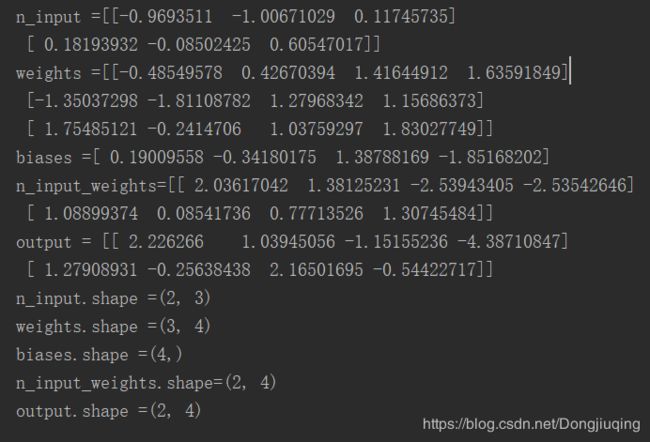
print("n_input ={} ".format(n_input))
print("weights ={} ".format(weights))
print("biases ={} ".format(biases))
print("n_input_weights={}".format(n_input_weights))
print("output = {}".format(output))
print("n_input.shape ={} ".format(n_input.shape))
print("weights.shape ={}".format(weights.shape))
print("biases.shape ={}".format(biases.shape))
print("n_input_weights.shape={}".format(n_input_weights.shape))
print("output.shape ={}".format(output.shape))把输出的结果拿出来自己感受一下。