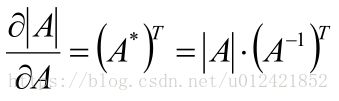ICA（独立成分分析）(1)

转载于：https://blog.csdn.net/u012421852/article/details/80500891

要容易理解ICA，就需要先好好理解透彻下面这些概率统计和线性代数的知识点：高斯分布、概率密度函数、累积分布函数、复合函数的概率密度函数、行列式、代数余子式、矩阵微积分等。下面一一简单记录和复习下这些概念，俗话说书读百遍其义自见，这里再多写一遍也不为过。

1.ICA概念

Independent Component Correlation Algorithm，ICA，独立成分分析算法，是一种函数。

X为n维观测信号矢量，S为独立的m维未知源信号矢量，矩阵A被称为混合矩阵。

ICA的目的就是寻找解混矩阵W（W=A的逆矩阵），然后对X进行线性变换，得到输出向量U = WX = WAS

主要应用于：表情分类

ICA详细的计算过程的原理推理，详见后面文章：点我

2.高斯分布

2.1名称

Normal Distribution，正态分布，也称常态分布，又名高斯分布（Gaussian Distribution）。是一个在数学、物理及工程等领域都非常重要的概率分布。

2.2正态分布

若随机变量X服从一个数学期望μ，方差为σ^2的正态分布，则记作N(μ，σ^2)。

随机变量X的概率密度函数为：μ决定了其位置，标准差σ决定了分布的幅度。

2.3标准正态分布

当μ=0，σ=1时的正态分布为标准正态分布。

2.4正态分布<--->标准正态分布

为了便于描述和应用，将正态变量X作为数据转换，将一般正态分布转化为标准正态分布：

X就是一般正态分布，Y就是由X转换来的标准正态分布。

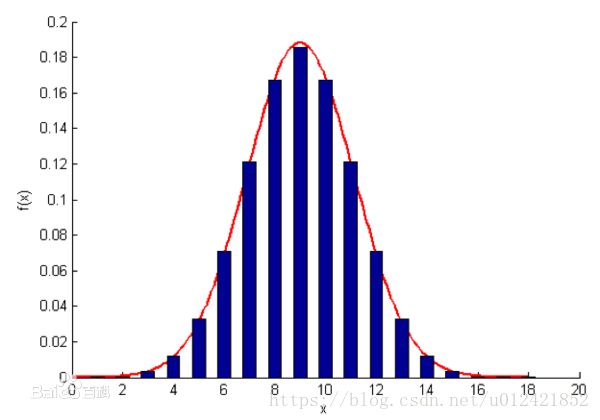
2.5正态分布几何形态

正态分布是一个概率分布，其形状神似一个倒扣的钟。

此图来自百度百科。

2.6一维正态分布的概率密度函数

若随机变量X服从一个数学期望μ，方差为σ^2的正态分布，则记作N(μ，σ^2)。则其概率密度函数为：

X被称为正态随机变量，称正态随机变量X服从的分布称为正态分布，记作，读作X服从，或者X服从正态分布。

2.7标准正态分布

当 时，正态分布就成为标准正态分布，标准正态分布的概率密度函数为：

3.概率密度函数

probability density function，概率密度函数，也可以称为密度函数，一般简写为小写的pdf。

注：概率密度函数 是连续型随机变量的；离散随机变量的，就是概率P(x)。

概率密度函数是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。

而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。

对于一维实随机变量X，设X的累积分布函数CDF是，如果存在可测函数满足：

  

那么X是一个连续型随机变量，并且  是X的概率密度函数。

密度函数f(x) 具有下列性质：

①  ；

②  ；

③ 

注：连续型的随机变量取值在任意一点的概率都是0；如果概率P{x=a}=0，但{X=a}并不是不可能事件。

4.复合函数的概率密度函数

X的概率密度f _X (x)，若Y = ax，a是某个正实数，求Y的概率密度

注：如果a是负实数，则给结论的第一个1/a加上绝对值

注：如果Y和X是向量，A是矩阵的话，结论第一个1/a就变成|A|^-1，第二个1/a就变成A^-1。

5.累积分布函数/分布函数

CDF，Cumluative Distribution Function，累积分布函数，又叫分布函数，是概率密度函数的积分，可以完整描述一个实随机变量X的概率分布。

概率分布：

    随机变量的概率分布，即随机变量的可能取值以及取得对应值的概率。

pdf和CDF：

    一般用大写的CDF标记累积分布函数，分布函数。一般用小写的pdf标记概率密度函数。

累积分布函数的概念公式为：

    

举例一个离散随机变量的累积分布函数/分布函数的几何图形：

此图来自百度百科

CDF的性质

（1）有界性

        

        

（2）单调性

        

（3）右连续性

        

（4）X取值落在区间(a,b]之内的概率：

        

（5）随机变量X的CDF和pdf的关系：

        

6.联合分布函数/多维分布函数

joint distribution function，联合分布函数、也称为多维分布函数，多维随机变量的分布函数。

设(X,Y)是二维随机变量，对于任意实数x,y，有二元函数F(x,y)：

    F(x,y) = P{(X<=x) 交 (Y<=y)} => P(X<=x, Y<=y)，

称F(X,Y)为二维随机变量(X,Y)的分布函数，或称为随机变量X和Y的联合分布函数。

几何意义

如果将二维随机变量（X,Y）看成是平面上随机点的坐标，那么联合分布函数F(X,Y)在(x,y)处的函数值就是随机点(X,Y)落在以(x,y)为顶点而位于该点左下方的无穷矩形区域内的概率。

二维离散随机变量X，Y的联合分布函数

            

则X,Y的概率分布函数一定满足：

            

7.行列式求导

注：

8.离散随机变量的分布律

    分布律描述了离散随机变量取每个值各占的概率

(end)