数据结构：红黑树的旋转原理和模拟实现

红黑树的旋转原理和模拟实现

我们了解到AVL树虽然效率很高，但是它是通过多次的旋转才到达一个绝对的平衡，旋转的消耗其实也很大。因此开始引入近似平衡的一棵树----红黑树（RBTree）。红黑树每一个节点不是红色的就是黑色的，它保证了最长路径不超过最短路径的二倍。

其实一般来说使用红黑树会比AVL树更多，因为虽然AVL树是更加平衡的，但是它的平衡是通过更多次的旋转得到的，旋转的时候消耗还是很大的。而红黑树是近似平衡的，它的旋转比AVL树要少。但是有人可能会有疑问，那红黑树的搜索效率没有AVL树高啊？其实他俩是差不多的，因为AVL树是O(logN)，而红黑树是O(2logN)，假如是十亿个数据的话，AVL树用30次查找，那么红黑树也就是60次查找，对于现在的计算机CPU计算速度来说是没有多大影响的，所以用红黑树用的会多一些。

红黑树的特点：

1. 根节点一定是黑色的
2. 一个红色节点的孩子只能是黑色的
3. 每一条路径上的黑色节点的个数相同
4. 每个节点不是红色的就是黑色的
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

根据这五个特点我们就可以推断出最长路径不超过最短路径的二倍。因为如果一颗树是红黑树，那么它的最短路径就是全黑节点的那一条路径，最长路径就是一个黑色一个红色这样红黑相间的路径。

红黑树节点的定义

enum Color//枚举颜色
{
	RED,
	BLACK,
};
template<class K,class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;//指向左树节点
	RBTreeNode<K, V>* _right;//指向右树节点
	RBTreeNode<K, V>* _parent;//指向父亲节点
    pair<K, V> _kv;
	Color _col;//颜色
};

红黑树的插入

红黑树的插入需要这么几步：

1. 如果是空树，那么直接让root等于这个新开节点，然后把这个节点的颜色变为黑色
2. 如果不是空树，那么就先去找要插入的位置，如果要插入的值比该节点小就去左边，比该节点大就去右边
3. 找到位置之后将该节点连接到树中，然后将这个新插入的节点设置为红色（为什么是设置为红色呢？ 因为如果插入一个黑色节点的话，那么就会破坏红黑树的每条路径上的黑色节点数目相同的这条性质，因为在你插入的这条路径上就会多出来一个黑色节点，那么就会影响到其他的路径，影响范围很大。但是如果插入的是红色节点，那么如果它的父亲是黑色就非常完美，不用对树进行修改，只有当它的父亲是红色才需要进行修改，因为两个红色的节点不能连接再一起。所以说如果插入黑色节点，必然一定会破坏所以路径，而插入红色的节点是有可能会破坏这条路径。）
4. 如果插入这个红色节点之后父亲也是红色，则对这颗树进行调整

如果要进行调整的的话分为以下几种情况，我们约定一下起名规则如下：
cur：新插入的节点
parent：新插入节点的父亲节点
uncle：新插入节点的叔叔节点
grandfather：新插入节点的祖父节点

情况一：插入节点为红色，父亲为红色，叔叔存在且为红色

如下图，新插入节点cur是红色，父亲也是红色，叔叔也是红色，那么祖父必然是一个黑色节点，那么把父亲和叔叔变成黑色，把祖父变成红色，然后这颗树上每条路径的黑色节点就都是一样的了。

但是这个步骤完成之后还需要继续往上判断，因为如果把祖父变成了红色，祖父还不是根节点的话，万一祖父的父亲也是红色节点就需要再次调整了，如下图。

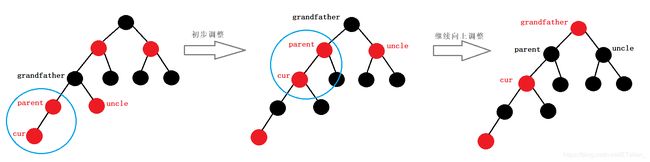
最后根据需要，如果grandfather为根节点的话直接把根变成黑色（因为根节点一定是黑色的）。

情况二：插入节点（左边）为红色，父亲为红，叔叔不存在/叔叔为黑

如果插入节点红色，父亲也是红色，那么祖父一定是黑色，此时如果没有叔叔节点的话，那就要进行旋转，如图情况，对这颗树进行右单旋，然后在进行变色，把祖父变成红色，把父亲变成黑色。

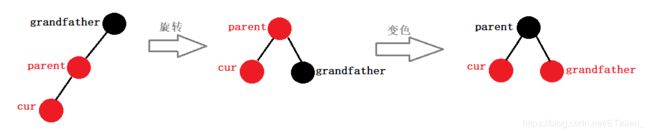
如果插入节点红色，父亲也是红色，那么祖父一定是黑色，此时如果叔叔节点为黑，那么应该怎么办呢？如果遇到叔叔节点为黑时，那一定是通过情况一演变上来的。如下图，当向上更新时，发现叔叔节点为黑，那么我们以parent为中心进行右单旋，把parent的左树变成grandfather的左树，然后再把grandfather变成parent的右树。

情况三：插入节点（右边）为红色，父亲为红，叔叔不存在/叔叔为黑

插入节点为红，父亲如果为红，祖父必然为黑，如果此时叔叔节点不存在，那么需要先以parent为中心进行左单旋，然后再交换cur和parent的指向（遵循我们制定的约定），然后再以grandfather为中心右单旋。

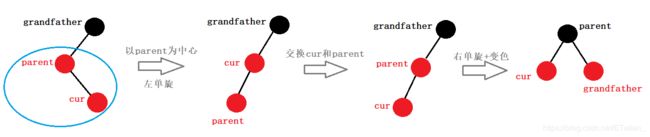
如果插入节点为红，父亲为红，祖父必然为红，此时叔叔节点为黑，那么必然是情况一演变而来的，首先以parent为中心进行左单旋，然后再交换parent和cur的指向，再以grandfather为中心进行右单旋，最后再讲parent变为黑色，grandfather变为红色。如下图：

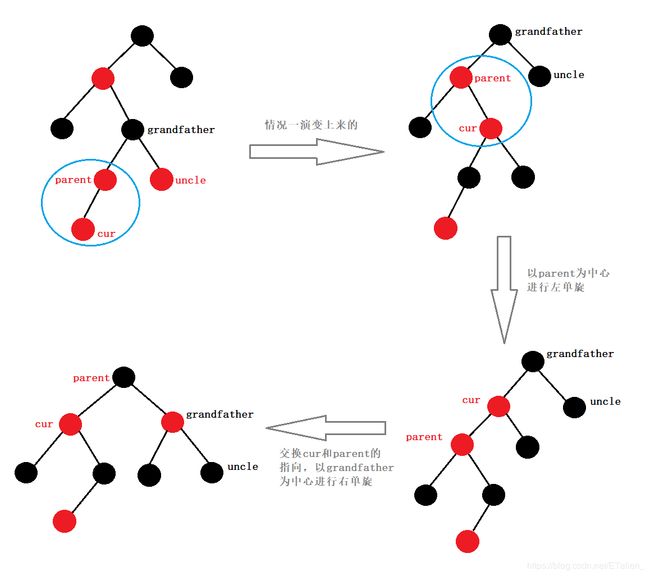
注：以上博主画的都是父亲在左边叔叔在右边的情况，反之叔叔在左边父亲在右边也是一样的啦
然后博主就不画了吧 |ू･ω･` )，画图太费眼睛啦！博主上面的图画了好久好久！
博主可能有强迫症！然后哇的一声就哭了 ﾍ(;´Д｀ﾍ)。

红黑树的左单旋右单旋和AVL树的左单旋右单旋一毛一样，还有遍历也是一毛一样！！！

好的！那么我们一起来看代码 ~ 嘻嘻嘻 ~

RBTree.h

#pragma once

#include 
using namespace std;

enum Color
{
	RED,
	BLACK,
};

template<class K,class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
    pair<K, V> _kv;
	Color _col;

	RBTreeNode(const pair<K, V> kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _col(RED)
	{}
};

template<class K,class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv)
	{
		//空树情况
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return true;
		}

		//不是空树的情况
		Node* parent = nullptr;
		Node* cur = _root;
		//找到位置
		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
				return false;
		}
		//新开节点，连接起来
		cur = new Node(kv);
		cur->_col = RED;
		if (parent->_kv.first > kv.first)
		{
			parent->_left = cur;
			cur->_parent = parent;
		}
		else
		{
			parent->_right = cur;
			cur->_parent = parent;
		}

		//进行调整树
		while(parent && parent->_col == RED)//parent存在且为红色
		{
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)//父亲在左边，叔叔在右边
			{
				Node* uncle = grandfather->_right;
				if (uncle && uncle->_col == RED)//叔叔存在且为红
				{
					//变色
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else//叔叔不存在或者为黑
				{
					//先处理双旋
					if (cur == parent->_right)
					{
						RotateL(parent);
						swap(cur, parent);
					}
					//单旋+变色
					RotateR(grandfather);
					parent->_col = BLACK;
					grandfather->_col = RED;
					break;
				}
			}
			else//grandfather->right == parent  父亲在右边，叔叔在左边
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)//叔叔存在且为红
				{
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else//叔叔不存在或者为黑
				{
					//先处理双旋
					if (cur == parent->_left)
					{
						RotateR(parent);
						swap(cur, parent);
					}
					//单旋+变色
					RotateL(grandfather);
					parent->_col = BLACK;
					grandfather->_col = RED;
					break;
				}
			}
		}
		_root->_col = BLACK;
		return true;
	}
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;
		subR->_left = parent;
		Node* ppnode = parent->_parent;
		parent->_parent = subR;
		if (_root == parent)
		{
			_root = subR;
		}
		else
		{
			if (ppnode->_left == parent)
				ppnode->_left = subR;
			else
				ppnode->_right = subR;
		}
		subR->_parent = ppnode;
	}
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;
		subL->_right = parent;
		Node* ppnode = parent->_parent;
		parent->_parent = subL;
		if (parent == _root)
		{
			_root = subL;
		}
		else
		{
			if (ppnode->_left == parent)
				ppnode->_left = subL;
			else
				ppnode->_right = subL;
		}
		subL->_parent = ppnode;
	}

	void _Inorder(Node* root)
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		cout << root->_kv.first << " ";
		_Inorder(root->_right);
	}
	void Inorder()
	{
		_Inorder(_root);
		cout << endl;
	}
private:
	Node* _root = nullptr;
};

void TestRBTree()
{
	RBTree<int, int> t;
	int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	for (auto e : a)
	{
		t.Insert(std::make_pair(e, e));
	}
	t.Inorder();
}

Test.cpp

#include "RBTree.h"
int main()
{
	TestRBTree();
	system("pause");
	return 0;
}