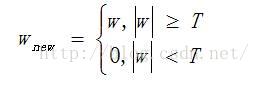数字图像处理,一维信号小波阈值去噪的C++实现
本文代码的实现严重依赖前面的一篇文章:
小波变换Mallat算法的C++实现
一,小波阈值去噪基本理论
1,小波阈值处理基本理论
小波阈值收缩法是Donoho和Johnstone在1995年提出的,以下便是养活不少学者的三篇基础论文,引得无数学者在此基础上优化,或者应用到自己的工程中然后发表相关的论文:
【1】 Donoho D L. De-noising by soft-thresholding. IEEE Trans- actions on Information Theory, 1995, 41(3): 613−627
【2】 Donoho D L, Johnstone I M. Adapting to unknown smooth- ness via wavelet shrinkage. Journal of the American Statistic
Association, 1995, 90(432): 1200−1224
【3】 Donoho D L, Johnstone I M, Kerkyacharian G, Picard D. Wavelet shrinkage: asymptopia? Journal of Royal Statisti-
cal Society Series B, 1995, 57(2): 301−369
所谓阈值去噪简而言之就是对信号进行分解,然后对分解后的系数进行阈值处理,最后重构得到去噪信号。该算法其主要理论依据是:小波变换具有很强的去数据相关性,它能够使信号的能量在小波域集中在一些大的小波系数中;而噪声的能量却分布于整个小波域内.因此,经小波分解后,信号的小波系数幅值要大于噪声的系数幅值.可以认为,幅值比较大的小波系数一般以信号为主,而幅值比较小的系数在很大程度上是噪声.于是,采用阈值的办法可以把信号系数保留,而使大部分噪声系数减小至零.小波阈值收缩法去噪的具体处理过程为:将含噪信号在各尺度上进行小波分解,设定一个阈值,幅值低于该阈值的小波系数置为0,高于该阈值的小波系数或者完全保留,或者做相应的“收缩(shrinkage)”处理.最后将处理后获得的小波系数用逆小波变换进行重构,得到去噪后的信号.
2,阈值函数的选取
小波分解阈值去噪中,阈值函数体现了对超过和低于阈值的小波系数不同处理策略,是阈值去噪中关键的一步。设w表示小波系数,T为给定阈值,sign(*)为符号函数,常见的阈值函数有:
硬阈值函数: (小波系数的绝对值低于阈值的置零,高于的保留不变)
软阈值函数: (小波系数的绝对值低于阈值的置零,高于的系数shrinkage处理)
值得注意的是:
1) 硬阈值函数在阈值点是不连续的,在下图中已经用黑线标出。不连续会带来振铃,伪吉布斯效应等。
2) 软阈值函数,原系数和分解得到的小波系数总存在着恒定的偏差,这将影响重构的精度
同时这两种函数不能表达出分解后系数的能量分布,半阈值函数是一种简单而经典的改进方案。见下图:
图1
3,阈值的确定
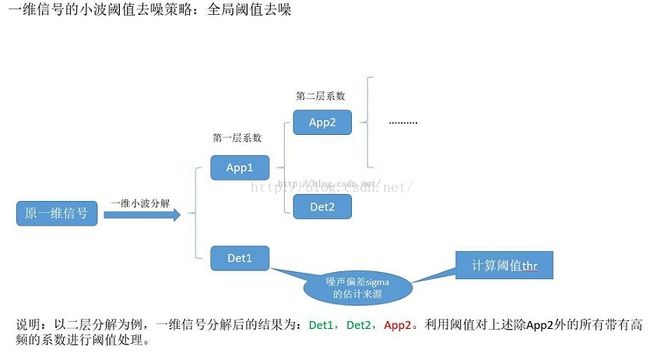
选取的阈值最好刚好大于噪声的最大水平,可以证明的是噪声的最大限度以非常高的概率低于![]() (此阈值是Donoho提出的),其中根号右边的这个参数(叫做sigma)就是估计出来的噪声标准偏差(根据第一级分解出的小波细节系数,即整个det1绝对值系数中间位置的值),本文将用此阈值去处理各尺度上的细节系数,注意所谓全局阈值就是近似系数不做任何阈值处理外,其他均阈值处理。
(此阈值是Donoho提出的),其中根号右边的这个参数(叫做sigma)就是估计出来的噪声标准偏差(根据第一级分解出的小波细节系数,即整个det1绝对值系数中间位置的值),本文将用此阈值去处理各尺度上的细节系数,注意所谓全局阈值就是近似系数不做任何阈值处理外,其他均阈值处理。
最后吐槽一下这个“绝对值系数中间位置的值”
1)如果det1的长度为偶数那么,这个“中值”便是中间位置的两个数之和的平均值,比如【2,2,3,5】,中值即是2.5而不是3
2)如果det1的长度为奇数那么,这个中值就是中间位置的那个数,比如【2,3,5】,中值即3
4,阈值策略
以前写的ppt挪用过来:
5,一维信号的多级分解与重构
以下算法如果用简单的文字描述,可是:先将信号对称拓延(matlab的默认方式),然后再分别与低通分解滤波器和高通分解滤波器卷积,最后下采样,最后可以看出最终卷积采样的长度为floor(n-1)/2+n,如果想继续分解下去则继续对低频系数CA采取同样的方式进行分解。二,matlab实现一维小波阈值去噪
1,核心库函数说明
1)wnoisest函数
作用:估计一维小波高频系数中的噪声偏差
这个估计值使用的是绝对值中间位置的值(估计的噪声偏差值)除以0.6745(Median Absolute Deviation / 0.6745),适合0均值的高斯白噪声
2)wavedec函数
一维信号的多尺度分解,将返回诸多细节系数和每个系数的长度,在matlab中键入“doc wavedec”具体功能一目了然
3)waverec函数
一维信号小波分解系数的重构,将返回重构后的信号在matlab中键入“doc waverec”具体功能一目了然,也可以键入“open waverec”查看matlab具体是怎么做的。
4)wdencmp函数
这个函数用于对一维或二维信号的压缩或者去噪,使用方法:
1 [XC,CXC,LXC,PERF0,PERFL2] = wdencmp('gbl',X,'wname',N,THR,SORH,KEEPAPP)
2 [XC,CXC,LXC,PERF0,PERFL2] = wdencmp('lvd',X,'wname',N,THR,SORH)
3 [XC,CXC,LXC,PERF0,PERFL2] = wdencmp('lvd',C,L,'wname',N,THR,SORH)
wname是所用的小波函数,
gbl(global的缩写)表示每层都采用同一个阈值进行处理,
lvd表示每层用不同的阈值进行处理,
N表示小波分解的层数,
THR为阈值向量,
对于格式(2)(3)每层都要求有一个阈值,因此阈值向量THR的长度为N,
SORH表示选择软阈值还是硬阈值(分别取为’s’和’h’),
参数KEEPAPP取值为1时,则低频系数不进行阈值量化处理,反之,则低频系数进行阈值量化。
XC是消噪或压缩后的信号,[CXC,LXC]是XC的小波分解结构,
PERF0和PERFL2是恢复和压缩L^2的范数百分比, 是用百分制表明降噪或压缩所保留的能量成分。
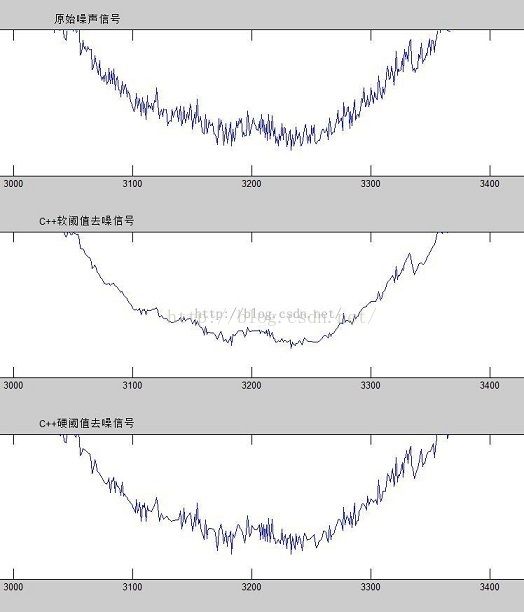
2,阈值去噪效果
从图中可以查出,除燥效果还是比较理想的,对于噪声比较重的地方软阈值去噪能力更加明显(因为没有无噪的信号参考,这并不能代表他比硬阈值更优秀)。
放大其中的细节部分,便于查看细节(抱歉,这里用了C++的处理结果,但是可喜的是他和matlab的结果一模一样)
3,完整的matlab代码
本代码就是上述效果的matlab程序!
clc;
clear;
% 获取噪声信号
load leleccum;
indx = 1:3450;
noisez = leleccum(indx);
%信号的分解
wname = 'db3';
lev = 3;
[c,l] = wavedec(noisez,lev,wname);
%求取阈值
sigma = wnoisest(c,l,1);%使用库函数wnoisest提取第一层的细节系数来估算噪声的标准偏差
N = numel(noisez);%整个信号的长度
thr = sigma*sqrt(2*log(N));%最终阈值
%全局阈值处理
keepapp = 1;%近似系数不作处理
denoisexs = wdencmp('gbl',c,l,wname,lev,thr,'s',keepapp);
denoisexh = wdencmp('gbl',c,l,wname,lev,thr,'h',keepapp);
% 作图
subplot(311),
plot(noisez), title('原始噪声信号');
subplot(312),
plot(denoisexs), title('matlab软阈值去噪信号') ;
subplot(313),
plot(denoisexh), title('matlab硬阈值去噪信号') ;三,C加加实现小波阈值去噪
说明:一维信号的单尺度分解在前一篇文章中已经提及,这里不再累述,这里主要再次基础上的多尺度分解与重构
并且在执行自己编写的wavedec函数时必须先初始化,初始化的目的是为了获取信号的长度,选择的是什么小波,以及分解的等级等信息,然后计算出未来的各种信息,比如每个等级的系数的size,为了进行一维小波分解的初始化函数如下:
bool CWavelet::InitDecInfo(
const int signalLen,//源信号长度
const int decScale,//分解尺度
const int decdbn//db滤波器的编号
)
{
if (decdbn != 3)
SetFilter(decdbn);
if (signalLen < m_dbFilter.filterLen - 1)
{
cerr << "错误信息:滤波器长度大于信号!" << endl;
return false;
}
int srcLen = signalLen;
m_msgCL1D.dbn = decdbn;
m_msgCL1D.Scale = decScale;
m_msgCL1D.msgLen.resize(decScale + 2);
m_msgCL1D.msgLen[0] = srcLen;
for (int i = 1; i <= decScale; i++)
{
int exLen = (srcLen + m_dbFilter.filterLen - 1) / 2;//对称拓延后系数的长度
srcLen = exLen;
m_msgCL1D.msgLen[i] = srcLen;
}
m_msgCL1D.msgLen[decScale + 1] = srcLen;
for (int i = 1; i < decScale + 2; i++)
m_msgCL1D.allSize += m_msgCL1D.msgLen[i];
m_bInitFlag1D = true;//设置为已经初始化
return true;
}1,核心函数的实现
1),信号的多级分解
注:本函数实现了对信号的任意级数分解(分解级数不是在此函数指定),分解的全部系数与matlab的结果完全一致
// 一维多尺度小波分解,必须先初始化
//分解的尺度等信息已经在初始化函数获取
bool CWavelet::WaveDec(
double *pSrcData,//要分解的信号
double *pDstCeof//分解出来的系数
)
{
if (pSrcData == NULL || pDstCeof == NULL)
return false;
if (!m_bInitFlag1D)
{
cerr << "错误信息:未初始化,无法对信号进行分解!" << endl;
return false;
}
int signalLen = m_msgCL1D.msgLen[0];
int decLevel = m_msgCL1D.Scale;
double *pTmpSrc = new double[signalLen];
double *pTmpDst = new double[m_msgCL1D.msgLen[1] * 2];
for (int i = 0; i < signalLen; i++)
pTmpSrc[i] = pSrcData[i];
int gap = m_msgCL1D.msgLen[1] * 2;
for (int i = 1; i <= decLevel; i++)
{
int curSignalLen = m_msgCL1D.msgLen[i - 1];
DWT(pTmpSrc, curSignalLen, pTmpDst);
for (int j = 0; j < m_msgCL1D.msgLen[i] * 2; j++)
pDstCeof[m_msgCL1D.allSize - gap + j] = pTmpDst[j];
for (int k = 0; k < m_msgCL1D.msgLen[i]; k++)
pTmpSrc[k] = pTmpDst[k];
gap -= m_msgCL1D.msgLen[i];
gap += m_msgCL1D.msgLen[i + 1] * 2;
}
delete[] pTmpDst;
pTmpDst = NULL;
delete[] pTmpSrc;
pTmpSrc = NULL;
return true;
}2),多级分解系数的重构
注:本函数只能还原成原始信号,还不能重构到某个中间分解结果
// 重构出源信号
bool CWavelet::WaveRec(
double *pSrcCoef,//源被分解系数
double *pDstData//重构出来的信号,两者的长度是一样的
)
{
if (pSrcCoef == NULL || pDstData == NULL)//错误:无内存
return false;
//从m_msgCL1D中获取分解信息
int signalLen = m_msgCL1D.msgLen[0];//信号长度
int decLevel = m_msgCL1D.Scale;//分解级数
int det1Len = m_msgCL1D.msgLen[1];
double *pTmpSrcCoef = new double[det1Len * 2];
for (int i = 0; i < m_msgCL1D.msgLen[decLevel] * 2; i++)
pTmpSrcCoef[i] = pSrcCoef[i];
int gap = m_msgCL1D.msgLen[decLevel] * 2;
for (int i = decLevel; i >= 1; i--)
{
int curDstLen = m_msgCL1D.msgLen[i - 1];
IDWT(pTmpSrcCoef, curDstLen, pDstData);
if (i != 1)
{
for (int j = 0; j < curDstLen; j++)
pTmpSrcCoef[j] = pDstData[j];
for (int k = 0; k < curDstLen; k++)
pTmpSrcCoef[k + curDstLen] = pSrcCoef[k + gap];
gap += m_msgCL1D.msgLen[i - 1];
}
}
delete[] pTmpSrcCoef;
pTmpSrcCoef = NULL;
return true;
}3),阈值的获取
注:严格依照Donoho的阈值写的代码
// 根据细节系数,以及信号长度计算阈值
double CWavelet::getThr(
double *pDetCoef,//细节系数(应该是第一级的细节系数)
int detLen,//此段细节系数的长度
bool is2D//当前细节系数是否来自是二维图像信号的
)
{
double thr = 0.0;
double sigma = 0.0;
for (int i = 0; i < detLen; i++)
pDetCoef[i] = abs(pDetCoef[i]);
std::sort(pDetCoef, pDetCoef + detLen);
if (detLen % 2 == 0 && detLen >= 2)
sigma = (pDetCoef[detLen / 2-1] + pDetCoef[detLen / 2]) / 2 / 0.6745;
else
sigma = pDetCoef[detLen / 2] / 0.6745;
if (!is2D)//一维信号
{
double N = m_msgCL1D.msgLen[0];
thr = sigma *sqrt(2.0*log(N));
}
else{//二维信号
double size = m_msgCL2D.msgHeight[0]*m_msgCL2D.msgWidth[0];
thr = sigma *sqrt(2.0*log(size));
}
return thr;
}4),高频系数阈值处理
注:本阈值函数只对高频系数做处理,不对近似系数处理
// 将系数阈值处理,一维二维均适用
void CWavelet::Wthresh(
double *pDstCoef,//细节系数(应该是除近似系数外的所有的细节系数)
double thr,//阈值
const int allsize,//分解出来的系数的总长度(非)
const int gap,//跳过最后一层的近似系数
SORH ish//阈值函数的选取
)
{
//
if (ish)//硬阈值
{
for (int i = gap; i < allsize; i++)
{
if (abs(pDstCoef[i]) < thr)//小于阈值的置零,大于的不变
pDstCoef[i] = 0.0;
}
}
else//软阈值
{
for (int i = gap; i < allsize; i++)
{
if (abs(pDstCoef[i]) < thr)//小于阈值的置零,大于的收缩
{
pDstCoef[i] = 0.0;
}
else
{
if (pDstCoef[i] < 0.0)
pDstCoef[i] = thr - abs(pDstCoef[i]);
else
pDstCoef[i] = abs(pDstCoef[i]) - thr;
}
}
}
}5),阈值去噪函数
注:本函数涉及到上面提及的多个函数,此函数是核心的对外接口
bool CWavelet::thrDenoise(
double *pSrcNoise,//源一维噪声信号
double *pDstData,//去噪后的信号
bool isHard//阈值函数的选取,有默认值
)
{
if (pSrcNoise == NULL || pDstData == NULL)
exit(1);
if (!m_bInitFlag1D)//错误:未初始化
return false;
double *pDstCoef = new double[m_msgCL1D.allSize];
WaveDec(pSrcNoise, pDstCoef);//分解出系数
int Det1Len = m_msgCL1D.msgLen[1];
int gapDet = m_msgCL1D.allSize - Det1Len;
double *pDet1 = new double[Det1Len];
for (int i = gapDet, j = 0; i < m_msgCL1D.allSize; i++, j++)
pDet1[j] = pDstCoef[i];
int gapApp = m_msgCL1D.msgLen[m_msgCL1D.Scale];//跳过最后一层的近似系数
double thr = getThr(pDet1, Det1Len);//获取阈值
Wthresh(pDstCoef, thr, m_msgCL1D.allSize, gapApp, isHard);//将细节系数阈值
WaveRec(pDstCoef, pDstData);//重构信号
delete[] pDstCoef;
pDstCoef = NULL;
delete[] pDet1;
pDet1 = NULL;
return true;
}2,函数正确性验证
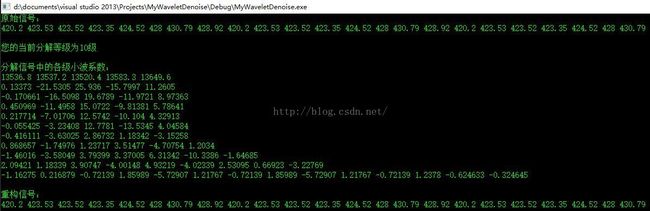
注:本次测试实现了对原始信号的10级分解,并与matlab进行了对比,结果完全一致(对比未完全展示)
以下数据为matlab的部分结果,完全相同于上述第二行,其他数据也完全一致。
3,对噪声信号阈值去噪
说明:C++处理的噪声信号数据先被保存为txt,该txt文件是由matlab加载导出的噪声信号,最后C++又将计算结果保存为txt,加载到matlab中显示。噪声去噪结果与matlab一致。
声明:
本文部分文字学习并整理自网络,部分代码参考于网络资源.
如果侵犯了您的版权,请联系本人[email protected],本人将及时编辑掉!
注:本博文为EbowTang原创,后续可能继续更新本文。本着共享、开源精神可以转载,但请务必复制本条信息!
原文地址:http://blog.csdn.net/ebowtang/article/details/40481393
原作者博客:http://blog.csdn.net/ebowtang
参考资源:
【1】网友,邹宇华,博客地址,http://blog.csdn.net/chenyusiyuan/article/details/2862768
【2】《维基百科----小波变换》
【3】乔世杰.小波图像编码中的对称边界延拓法[ J].中国图像图形学报,2000,5(2):725-729.
【4】MALLAT S.A theory formulti-resolution signal decompo-sition: the wavelet representation[ J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1989, 11(4):674-693.
【5】《小波十讲》
【6】《小波与傅里叶分析基础》
【7】冈萨雷斯《数字图像处理》
【8】matlab小波算法说明文档
【9】阈值去噪鼻祖论文,Donoho, D.L. (1995), "De-noising by soft-thresholding," IEEE Trans. on Inf. Theory, 41, 3, pp. 613–627.