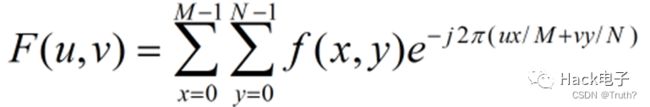红外图像处理算法介绍
大纲:
1.红外图像增强研究背景和意义
2.红外图像增强经典算法
1-红外图像增强研究背景和意义
1.1研究背景
红外图像是红外技术与成像技术结合的产物。人类感知只限于电磁波谱的可见光波段,对于全部电磁波谱上其它不可见光,如γ射线、X射线、紫外线、红外线、微波等,人类的视觉则无法感知。然而科学技术的发展使得成像技术与设备可以覆盖几乎全部电磁波谱,从γ射线到无线电波,将人类不可见的射线转化为可见的图像,这些图像涉及我们人类生活的许多领域,发挥着日益重要的作用。
比如,红外成像技术可以用于测温、监控着火、军事、检测建筑材料、医学、电力行业等。
1.2研究意义
但由于红外图像的成像机理以及红外成像系统自身的原因,红外图像与可见光图像相比,大多有图像对比度低、图像较模糊、信噪比低等特点。这对后续的特征提取、识别或跟踪等极为不利,因此抑制噪声,提高图像信噪比,以及调整红外图像对比度,增强红外图像边沿及线条等操作是必不可少的。所以,需要对图像进行适当的处理,因此红外图像增强是非常有必要的。
图像增强技术的主要目的是处理一幅给定的图像使它的结果对某种特定应用来说比原始。图像更合用。通过增强,可以改善红外图像的质量,为后续对红外图像的操作提供准备。
1.3红外图像的缺点
(1)红外热图像表征景物的温度分布,是灰度图像,没有彩色或阴影,分辨率低、分辨潜力差;
(2) 红外图像空间相关性强、对比度低、视觉效果模糊;
(3) 红外图像的清晰度低于可见光图像;
(4)外界环境的随机干扰和热成像系统的不完善,给红外图像带来多种多样的噪声,导致红外图像的信噪比非常低;
(5)外界干扰造成红外图像的非均匀性,体现为图像的固定图案噪声、串扰、 畸变等。
1.4红外成像技术的特点
(1)红外辐射能够穿过雾、烟尘而且系统工作波段宽,系统作用距离远;
(2)采取被动工作方式,不易被发现或受干扰;
(3)可在昼夜或恶劣气候下工作,接近全天候;
(4)适合高精度跟踪瞄准;
(5)不易受射击、爆炸和照明闪光等强光影响。
上述这些特点使红外热成像系统特别适合军事应用,因此,各国都以巨额投资竞相开展这一领域的研究工作。
2-红外图像增强经典算法
2.1图像增强
图像增强是指根据特定的需要突出图像中的重要信息,同时减弱或去除不需要的信息。从不同的途径获取的图像,通过进行适当的增强处理,可以将原本模糊不清甚至根本无法分辨的原始图像处理成清晰的富含大量有用信息的可使用图像,有效地去除图像中的噪声、增强图像中的边缘或其他感兴趣的区域,从而更加容易对图像中感兴趣的目标进行检测和测量。
有效地去除图像中的噪声、增强图像中的边缘或其他感兴趣的区域,从而更加容易对图像中感兴趣的目标进行检测和测量。
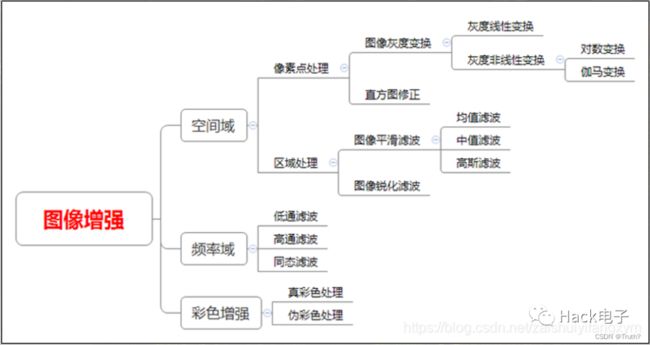
2.2灰度变换
基于点运算的灰度级矫正可以表示为:
g(x , y) = T[f(x , y)]
其中f表示灰度,T表示灰度变化函数。
根据T的不同,我们可以把灰度变换分为逆反处理、阈值变换、灰度拉伸、灰度切分、灰度级修正、动态范围调整等等。
总的来说分为线性变换和非线性变换。
2.2.1线性变换
G(,)=((−)/(−)∗((,)−)+)
(1)其中[a,b]表示原始图像的灰度范围,[c,d]表示变换后图像的灰度范围。

(2)特别地,令c=b=255,a=d=0,就实现了图像灰度反转。
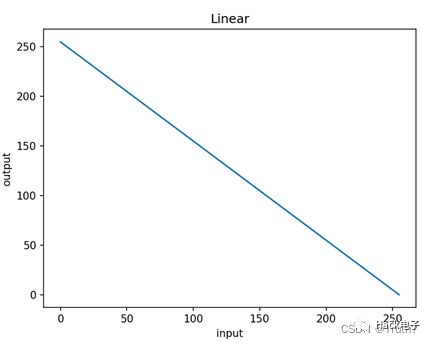

通过灰度反转,可以把感兴趣的目标突出出来。
(3)此外还有分段线性拉伸:
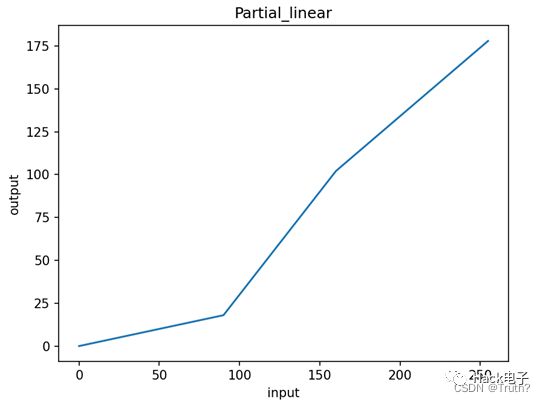

2.2.2非线性变换
包括指数变换(gamma变换)和对数变换等。
(1)指数变换

其中,a,b,c都是可以选择的参数
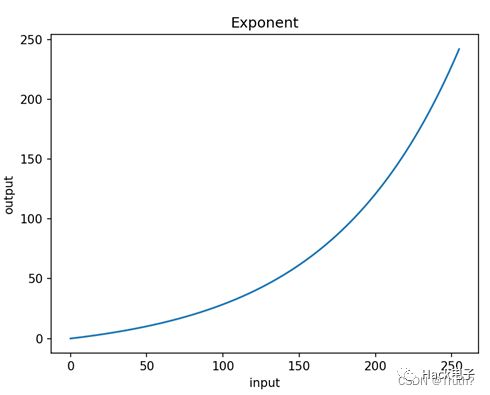
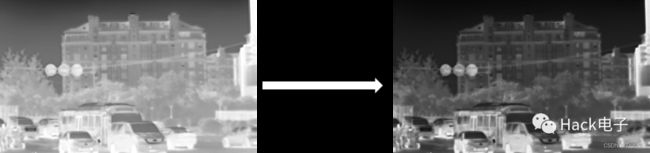
指数变换用于扩展高灰度区,一般适于过亮的图像。
(2)对数变换

其中a,b,c都是可选参数。

对数变换用于扩展低灰度区,一般适用于过暗的图像。
2.3直方图处理
直方图:
灰度直方图反映了数字图像中每一灰度级与其出现频率之间的统计关系。
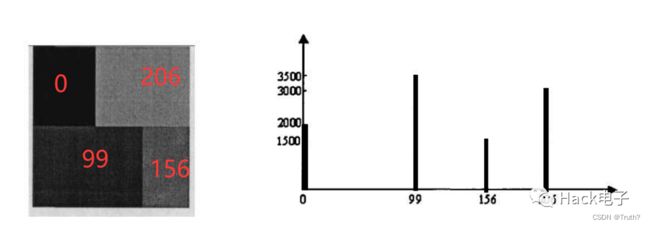
灰度直方图也可以用各灰度值出现的相对频数(该灰度级的像素数与图像总像素数之比)来表示。

其中n_k 表示灰度级r_k 出现的像素个数,n表示总像素个数
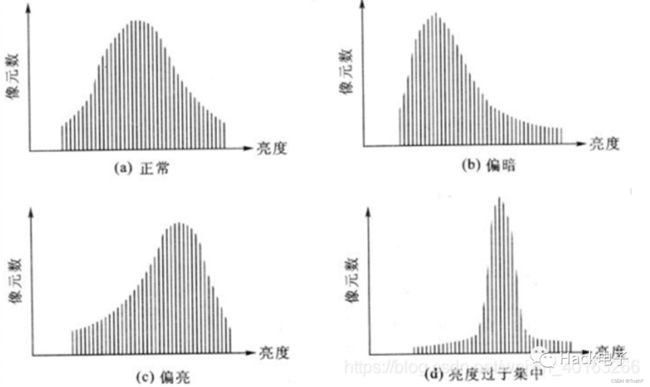
2.3.1直方图均衡化
传统的直方图均衡化把原图像的直方图通过灰度变换函数修正为灰度均匀分布的直方图以修正原图像。
当图像的直方图为一均匀分布时,图像的信息嫡最大,此时图像包含的信息量最大,图像看起来就显得清晰。
通常采用的灰度变换函数为:

r和s分别表示原始图像和增强后图像的灰度值,L表示灰度等级。
(1)数学表现
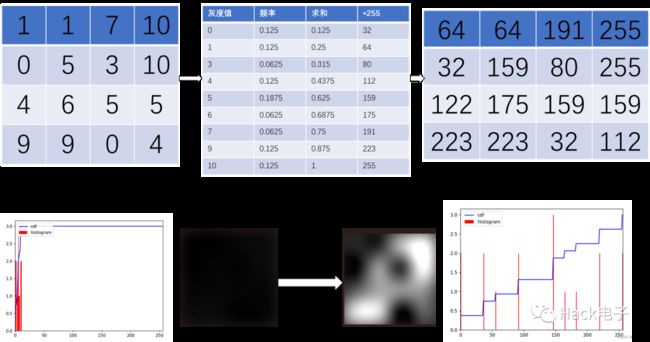
(2)全局均衡案例:
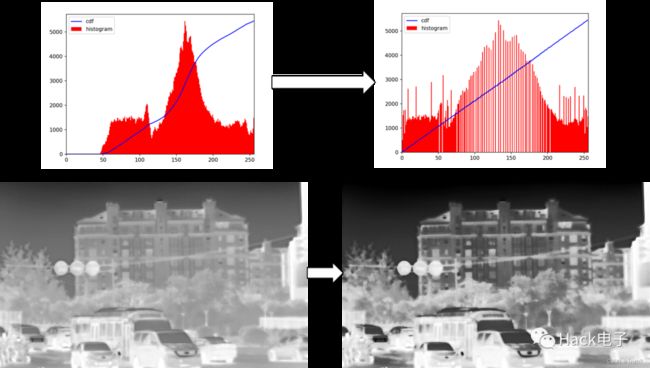
(3)局部直方图均衡化

利用全局增强方法对图像进行增强时,就不一定能保证我们所感兴趣的小区域得到所期望的增强效果,但局部均衡就能解决这个问题。
方法是将图像划分为不重叠的小块,在每一块进行直方图均衡化。
2.3.2直方图匹配(直方图规定化)
对于某些应用,采用直方图均衡的基本增强并不是最好的方法,特别地,有时我们希望处理后的图像具有规定的直方图形状,这种用于产生处理后有特殊直方图的方法称为直方图匹配或直方图规定化。
步骤:
(1)对原始图像的灰度直方图进行均衡化,由原始灰度rk得到灰度sk
(2)对规定的直方图进行均衡化,由原始灰度zq得到灰度vq
(3)对于每一个sk值,都寻找相应的vq值,使得vq最接近sk,进而可得sk到zq的映射。当满足sk的zq值多于一个时,我们选择最小的zq值进行映射。
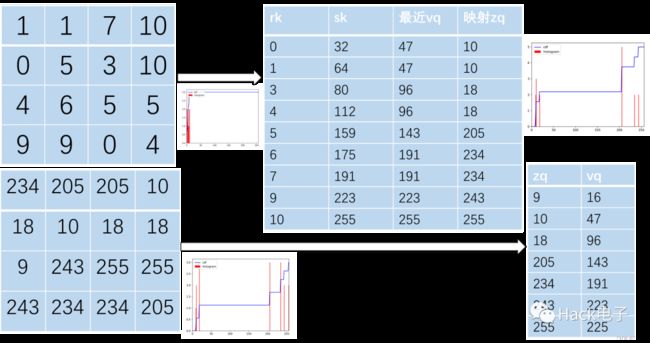

2.4图像平滑滤波
平滑滤波的目的主要是用来去除噪声或者失真,分为均值滤波,中值滤波和高斯滤波。
2.4.1均值滤波
典型的线性滤波算法,也是一种低通滤波器,高频信号将会被去掉,是指用当前像素点周围nn个像素值的均值来代替当前像素值。
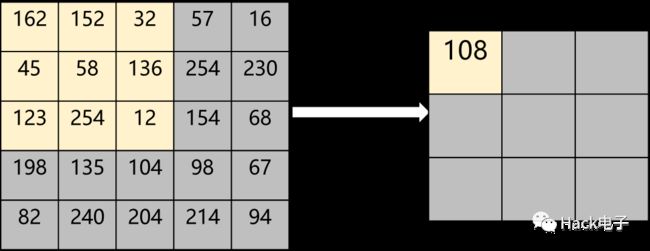

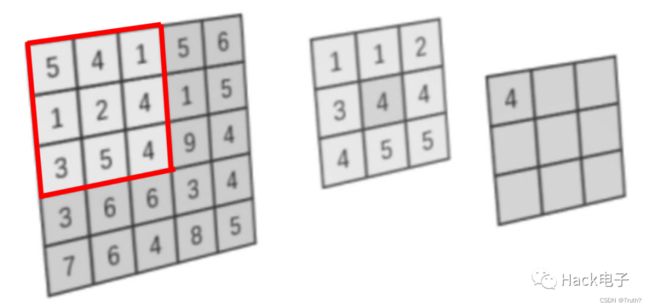
2.4.2中值滤波
中值滤波的原理是将已选择的某一像素点的邻域内(nn)的各像素点的值进行排序,并筛选中值作为当前像素点的数值,通过这种方式消除图像中色差、灰度值极大的像素值,从而减少噪声对图像的干扰。

2.4.3高斯滤波
高斯滤波属于线性平滑滤波,主要用于消除高斯噪声(高斯噪声的幅度分布服从正态分布),它的效果取决于高斯核的大小。
特别地,高斯滤波器的模板系数随着距离模板中心距离的增大,系数减小。所以,高斯滤波器相比于均值滤波器而言,对图像模糊程度较小,更能保持图像的整体细节。
需要确定权值分布函数,分布函数需要描述某像素点与高斯核中心点的相关性强度。
分布函数:

其中(x,y)为掩膜内任一点的坐标,(ux,uy)为掩膜内中心点的坐标,公式计算的结果作为权值。
为了方便解释,取欧氏距离为分布函数



2.4.4双边滤波
双边滤波(Bilateral Filters)是非常常用的一种滤波,它可以达到保持边缘、降噪平滑的效果。和其他滤波原理一样,双边滤波也是采用加权平均的方法,用周边像素亮度值的加权平均代表某个像素的强度,所用的加权平均基于高斯分布。
双边滤波的核函数是空间域核与像素范围域核的综合结果:在图像的平坦区域,像素值变化很小,对应的像素范围域权重接近于1,相当于进行高斯模糊;在图像的边缘区域,像素值变化很大,像素范围域权重变大,从而保持了边缘的信息。



2.4.5图像锐化滤波
图像锐化是和平滑相反的操作,目的是为了使模糊的图像变得清晰。既然是相反的目的,那么操作应该也是相反的,平滑使用的是图像邻域的加权求和或者是积分运算,而锐化则是使用求导数(梯度)或有限差分来实现。实现图像锐化首先需要提取图像边缘。
(1)二维连续函数情况下:
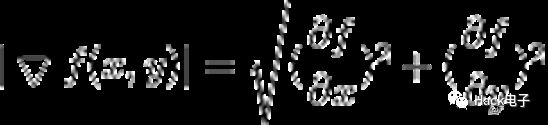
(2)二维离散函数情况下:

Laplacian算子:
基本思想是当邻域的中心像素灰度低于它所在邻域内的其他像素的平均灰度时,此中心像素的灰度应该进一步降低;当高于时进一步提高中心像素的灰度,从而实现图像锐化处理。


Sobel算子:
Sobel算子是一种用于边缘检测的离散微分算子,它结合了高斯平滑和微分求导。Sobel算子的边缘定位更准确,常用于噪声较多、灰度渐变的图像。Sobel算子根据像素点上下、左右邻点灰度加权差,在边缘处达到极值这一现象来检测边缘。


2.4.6低通滤波和高通滤波
图像在频域里面,频率低的地方说明它是比较平滑的,因为平滑的地方灰度值变化比较小,而频率高的地方通常是边缘或者噪声,因为这些地方往往是灰度值突变的。
所谓高通滤波就是保留频率比较高的部分,即突出边缘;低通滤波就是保留频率比较低的地方,即平滑图像,弱化边缘,消除噪声。
傅里叶变换:
傅里叶变换是将时间域上的信号转变为频率域上的信号,进而进行图像去噪、图像增强等处理。
对二维图像进行傅里叶变换用如下式子进行: