Codeforces Round #442 (Div. 2) E. Danil and a Part-time Job
E. Danil and a Part-time Job
Problem Statement
Danil decided to earn some money, so he had found a part-time job. The interview have went well, so now he is a light switcher.
Danil works in a rooted tree (undirected connected acyclic graph) with n vertices, vertex 1 is the root of the tree. There is a room in each vertex, light can be switched on or off in each room. Danil’s duties include switching light in all rooms of the subtree of the vertex. It means that if light is switched on in some room of the subtree, he should switch it off. Otherwise, he should switch it on.
Unfortunately (or fortunately), Danil is very lazy. He knows that his boss is not going to personally check the work. Instead, he will send Danil tasks using Workforces personal messages.
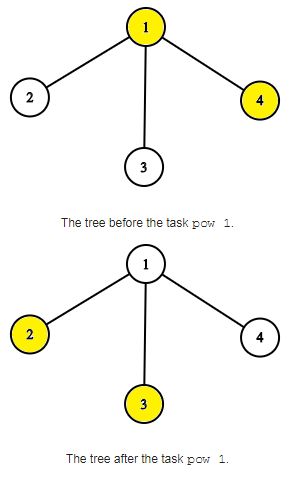
There are two types of tasks:1. pow v describes a task to switch lights in the subtree of vertex v.
2. get v describes a task to count the number of rooms in the subtree of v, in which the light is turned on. Danil should send the answer to his boss using Workforces messages.A subtree of vertex v is a set of vertices for which the shortest path from them to the root passes through v. In particular, the vertex v is in the subtree of v.
Danil is not going to perform his duties. He asks you to write a program, which answers the boss instead of him.
Input
The first line contains a single integer n (1 ≤ n ≤ 200 000) — the number of vertices in the tree.
The second line contains n - 1 space-separated integers p2 , p3 , …, pn (1 ≤ pi < i), where pi is the ancestor of vertex i.
The third line contains n space-separated integers t1 , t2 , …, tn (0 ≤ ti ≤ 1), where ti is 1, if the light is turned on in vertex i and 0 otherwise.
The fourth line contains a single integer q (1 ≤ q ≤ 200 000) — the number of tasks.
The next q lines are get v or pow v (1 ≤ v ≤ n) — the tasks described above.
Output
For each task get v print the number of rooms in the subtree of v, in which the light is turned on.
Examples
Example 1
Input
4
1 1 1
1 0 0 1
9
get 1
get 2
get 3
get 4
pow 1
get 1
get 2
get 3
get 4
Output
2
0
0
1
2
1
1
0
Note
题意
给一颗以节点1为根的树,每个节点上有一盏灯泡,现在给出树的连边情况,和灯泡的初始亮暗状态,有两种操作,第一种操作是将这个节点和这个节点的子树里的所有节点上的灯泡进行翻转(将暗的变成亮的,将亮的变成暗的),另一种操作是询问这个节点的子树(含这个节点)中有几盏亮的灯泡。
思路
一看到是对一颗子树的操作,我们就可以想到根据DFS序来做这题,不过显然,暴力是绝对不能过的。又因为两个操作在DFS序上分别对应区间反转和区间求和,我们很容易就能想到,用线段树维护就行了。所以这题就是DFS序+线段树。
Code
#pragma GCC optimize(3)
#includeint v=G[u][i];
if(v==fa[u])
continue;
dfs(v);
}
ed[u]=clo;
}
int main() {
read(n);
for(int i=2;i<=n;i++) {
read(fa[i]);
G[fa[i]].push_back(i);
}
dfs(1);
for(int i=1;i<=n;i++) {
read(b[i]);
a[st[i]]=b[i];
}
build(1,1,n);
// for(int i=1;i<=n;i++)
// cout<
read(q);
while(q--) {
cin>>s;
read(idx);
if(s=="pow")
update(1,1,n,st[idx],ed[idx]);
else
writeln(query(1,1,n,st[idx],ed[idx]));
}
return 0;
}