房价预测：回归问题

还有一种常见的机器学习问题是回归问题，它预测的是连续值而不是离散标签，例如，根据气象数据预测明天气温，或者根据软件说明书预测项目完成所需要的时间。

数据介绍

这里我们介绍一下数据。要预测的是是20世纪70年代波士顿房屋价格的中位数。这里给出的数据包括犯罪率、当期房产税率等。本次，我们有的数据点相对较少，只有506个，分为404个训练样本和102个测试样本。输入数据的每个特征都有不同的取值范围。有些特征是比例，取值范围为0-1，有的特征取值范围为1-12；还有的特征取值范围为0-100等。

from keras.datasets import boston_housing

(train_data, train_targets), (test_data, test_targets) =  boston_housing.load_data()

train_data.shape

test_data.shape

结果分别是：
(404, 13)
(102, 13)

这里每个样本有13个特征，比如犯罪率、每个住宅平均房屋间数、告诉公路的可达性等。

我们的目标（或者说希望的测试结果）是房屋价格的中位数，单位是千美元

train_targets

array([ 15.2, 42.3, 50. , 21.1, 17.7, 18.5, 11.3, 15.6, 15.6,
14.4, 12.1, 17.9, 23.1, 19.9, 15.7, 8.8, 50. , 22.5,
24.1, 27.5, 10.9, 30.8, 32.9, 24. , 18.5, 13.3, 22.9,…

---

对数据格式进行处理

将取值范围差异很大的数据直接输入到神经网络中，虽然网络会自动适应这种取值范围不同的数据，但是不进行数据处理直接学效果很不好。因为数据差异比较大的数据在网络中会整体学习效果有较大影响，所以我们需要先做标准化处理（0-1标准差）。

mean = train_data.mean(axis=0)  # axis = 0表示变成一行，实际上是求每列均值
train_data -= mean
std = train_data.std(axis=0)
train_data /= std

test_data -= mean
test_data /= std

---

构建网络

由于样本很小，所以我们用一个非常小的网络，其中包含两个隐藏层，每层有64个单元，一般来说，训练数据越少，过拟合就会越严重，而较小的网络可以降低过拟合。

from keras import models
from keras import layers

def build_model():
    # Because we will need to instantiate
    # the same model multiple times,
    # we use a function to construct it.
    model = models.Sequential()
    model.add(layers.Dense(64, activation='relu',
                           input_shape=(train_data.shape[1],)))
    model.add(layers.Dense(64, activation='relu'))
    model.add(layers.Dense(1))
    model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
    return model

网络的最后一层只有一个单元，没有激活，是一个线性层。这是标量回归（标量回归是预测单一连续值的回归）的典型设置。添加激活函数将会限制输出范围。例如，如果向最后一层添加sigmoid激活函数，网络只学会预测0-1范围内的值。这里最后一层是纯线性的，所以网络可以学会预测任何范围内的值。

这里，我们使用了mse损失函数（均方误差），这是回归问题常用的损失函数。

---

K折交叉验证

由于我们数据点很小，验证集会非常小（比如大约100个样本）。因此，验证分数可能会有很大波动，不同划分的结果可能会对数据产生较大的影响，所以我们使用K折交叉验证。

import numpy as np

k = 4
num_val_samples = len(train_data) // k
num_epochs = 100
all_scores = []
for i in range(k):
    print('processing fold #', i)
    # Prepare the validation data: data from partition # k
    val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
    val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]

    # Prepare the training data: data from all other partitions
    partial_train_data = np.concatenate(
        [train_data[:i * num_val_samples],
         train_data[(i + 1) * num_val_samples:]],
        axis=0)
    partial_train_targets = np.concatenate(  # concatenate合并两个array数组，按行合并，axis =0 ，竖着合并
        [train_targets[:i * num_val_samples],
         train_targets[(i + 1) * num_val_samples:]],
        axis=0)

    # Build the Keras model (already compiled)
    model = build_model()
    # Train the model (in silent mode, verbose=0)
    model.fit(partial_train_data, partial_train_targets,
              epochs=num_epochs, batch_size=1, verbose=0)
    # Evaluate the model on the validation data
    val_mse, val_mae = model.evaluate(val_data, val_targets, verbose=0)
    all_scores.append(val_mae)

我们这里设置迭代次数为100，运行结果如下：

all_scores

[2.0750808349930412, 2.117215852926273, 2.9140411863232605, 2.4288365227161068]

np.mean(all_scores)

2.3837935992396706
可以看到，经过4折交叉验证之后，预测结果和真实房间基本相差2400美元。

我们下面做500轮次，并修改最后一部分代码：

from keras import backend as K

# Some memory clean-up
K.clear_session()

num_epochs = 500
all_mae_histories = []
for i in range(k):
    print('processing fold #', i)
    # Prepare the validation data: data from partition # k
    val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
    val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]

    # Prepare the training data: data from all other partitions
    partial_train_data = np.concatenate(
        [train_data[:i * num_val_samples],
         train_data[(i + 1) * num_val_samples:]],
        axis=0)
    partial_train_targets = np.concatenate(
        [train_targets[:i * num_val_samples],
         train_targets[(i + 1) * num_val_samples:]],
        axis=0)

    # Build the Keras model (already compiled)
    model = build_model()
    # Train the model (in silent mode, verbose=0)
    history = model.fit(partial_train_data, partial_train_targets,
                        validation_data=(val_data, val_targets),
                        epochs=num_epochs, batch_size=1, verbose=0)
    mae_history = history.history['val_mean_absolute_error']
    all_mae_histories.append(mae_history)

下面我们可以计算每个轮次中所有折MAE的平均值。

average_mae_history = [
    np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]

---

画图

import matplotlib.pyplot as plt

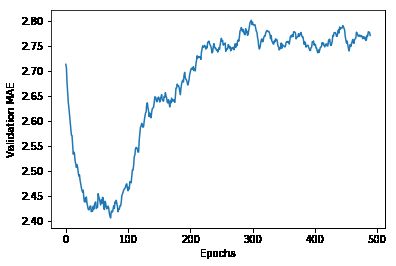
plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

这里，我们看到纵轴范围比较大，而且数据方差比较大，这张图所表达的规律不太明显。所以我们：

• 删除前10个点

• 将每个数据点替换为前面数据点的移动平均值，来得到光滑曲线

def smooth_curve(points, factor=0.9):
    
    smoothed_points = []
    for point in points:
        
        if smoothed_points:
            previous = smoothed_points[-1]
            smoothed_points.append(previous * factor + point * (1 - factor))
        else:def smooth_curve(points, factor=0.9):
            smoothed_points = []
    for point in points:
        if smoothed_points:
            previous = smoothed_points[-1]
            smoothed_points.append(previous * factor + point * (1 - factor))
        else:
            smoothed_points.append(point)
    return smoothed_points

smooth_mae_history = smooth_curve(average_mae_history[10:])

plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

从图中可以看出，验证MAE在80轮后不再显著下降，之后开始出现过拟合。

---

训练最终模型

我们得到最佳迭代次数这个超参数，大概是80，下面在全部训练集上训练结果

# Get a fresh, compiled model.
model = build_model()
# Train it on the entirety of the data.
model.fit(train_data, train_targets,
          epochs=80, batch_size=16, verbose=0)
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)

结果是：

test_mae_score

2.5532484335057877

预测房价和实际值大概相差2550元。

更多精彩内容，欢迎关注我的微信公众号：数据瞎分析