Frequency Filters-2

matlab的fft2函数可以实现求解图像的DFT，比如下面的这张图片，

通过matlab可以获得它的DFT图像（frequency spectrum）

img = rgb2gray(im);
>> ft = fft2(img);
>> imshow(log(abs(ft)),[]);

按照前面章节的说明，当前显示的结果同时覆盖了四个循环区域，使用fftshift函数进行调整，得到如下图示，

>> fts = fftshift(ft);
>> imshow(log(abs(fts)),[]);

图示中，中间高亮部分是低频部分，由中间向四周频率越来越高，低频对应的是图像中梯度平缓的地方，而高频对应的是图像中梯度较大的地方，如边缘等。我们发现，在DFT结果中，存在明显的“十字”形状，这主要是由于DFT的周期性导致图像拼接处存在强烈的色差形成较大梯度区域，从下图的红色框区域内可明显看出。

再看下面这个图像，左侧为原图像，中间为shift之后的图像（不存在明显的过渡边缘），右侧为对应的DFT图像，相比于前面的图像来说，则不存在这种边缘现象。

---

我们先来介绍下频率域滤波的基本步骤：

---

接下来，将介绍几种低通滤波和高通滤波应用，低通滤波可以保留图像的低频信息而丢弃部分高频信息，由于高频信息对应于图像中梯度变化较大的区域，如边缘等，所以低通滤波的效果实际上是等同于图像平滑效果；同样的，可以推测高通滤波则等同于图像的边缘提取。

低通滤波
三种常见的低通滤波：理想低通滤波（ILPF）、Butterworth低通滤波(BLPF)以及高斯低通滤波(GLPF)。

1.理想低通滤波：理想低通滤波的原理很简单，它只是简单地截断频谱上半径区域 D0 外所有的频率信息，而完全保留 D0 内的低频信息。滤波函数定义为，

H(u,v)={10D(u,v)≤D0D(u,v)>D0

其中， D0 为截断半径， D(u,v) 为频谱上点 (u,v) 与频谱中心 (P/2,Q/2) 的距离，以下公式中符号意义相同，

D(u,v)=(u−P/2)2+(v−Q/2)2−−−−−−−−−−−−−−−−−−−√

2.Butterworth低通滤波：
Butterworth的基本形式为，

H(u,v)=11+[D(u,v)/D0]2n

3.高斯低通滤波：
Butterworth的基本形式为，

H(u,v)=e−D2(u,v)/2D20

我们先来比较三种低通滤波的基本形状，

Butterworth低通滤波和高斯低通滤波相比于理想低通滤波而言，边界过度较为平滑，我们再来看三种滤波函数作用于图像频域率后的平滑效果，

原图为

仔细比较，可以发现理想低通滤波图像中，存在“波形”，尤其沿建筑边缘处较为明显。这种“blurring&ringing”现象是理想低通滤波存在的重要弊端。实际上，Butterworth低通滤波也有可能存在“ringing”现象，当Butterworth低通滤波公式中的n取值越大时，这种“ringing”现象会变得尤为明显。所以，通常Butterworth低通滤波取较小n值，以避免“ringing”现象的出现。

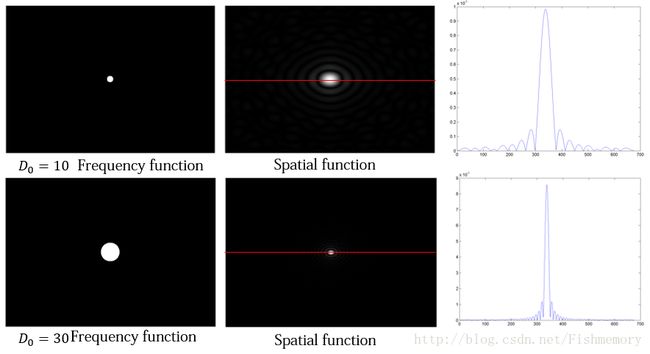
理想低通滤波中，“ringing”现象的产生实际上是与滤波函数本身有关的，理想低通滤波函数的基本形状类似于脉冲函数，转换至空间域后，函数形状类似于sinc波形。下图分别展示了截断半径分别为10和20频率域上的滤波函数（第一列）与空间上相应的滤波函数（第二列），以及空间域上红线处的像素值大小（第三列）。空间域上函数最中间的高峰值是图像平滑的主要原因，而外侧的小波形则是导致滤波图像“ringring”的主要原因。另外，我们可以发现，频率域上截断半径越大，转换至空间域上函数波形越密集。

高通滤波
高通滤波与低通滤波正好是相反的过程，保留高频信息，去掉低频信息，从而获得图像的边缘信息。与低通滤波相似，这里也只列出三种高通滤波：理想高通滤波、Butterworth高通滤波以及高斯高通滤波。

1.理想低通滤波：

H(u,v)={01D(u,v)≤D0D(u,v)>D0

2.Butterworth低通滤波：
Butterworth的基本形式为，

H(u,v)=11+[D0/D(u,v)]2n

3.高斯低通滤波：
Butterworth的基本形式为，

H(u,v)=1−e−D2(u,v)/2D20

三种滤波函数的基本形状，

以及滤波效果，

与低通滤波相似，理想高通滤波也存在“ringing”现象。

function filter_img = fft_smothing(img, method, thred)
[rows,cols,chls] = size(img);
if chls == 3
   img = rgb2gray(img); 
end

%DFT
ft = fft2(img);
ftshift = fftshift(ft);

if strcmp(method,'ideal')
    filter = ideal_lowpass_filter(thred, rows, cols);

elseif strcmp(method, 'butterworth')
    n = 2;
    filter = butterworth_lowpass_filter(thred, rows, cols, n);

elseif strcmp(method, 'Gaussian')
    filter = Gaussian_lowpass_filter(thred, rows, cols);
else
    fprintf('No such smothing type!');   
end

tran_frequency = ftshift.*filter;
filter_img = ifft2(tran_frequency);

end

function filter = ideal_lowpass_filter(thred, rows, cols)
    or = floor(rows/2);
    oc = floor(cols/2);

    [cidx,ridx] = meshgrid(1:cols,1:rows);

    filter_val = @(x) x <= thred;
    cshift = bsxfun(@minus, cidx, oc);
    rshift = bsxfun(@minus, ridx, or);
    filter = arrayfun(filter_val,sqrt(cshift.*cshift + rshift.*rshift));
end

function filter = butterworth_lowpass_filter(thred, rows, cols, n)
    or = floor(rows/2);
    oc = floor(cols/2);

    [cidx,ridx] = meshgrid(1:cols,1:rows);

    filter_val = @(x) 1/(1+(x/thred)^(2*n));
    cshift = bsxfun(@minus, cidx, oc);
    rshift = bsxfun(@minus, ridx, or);
    filter = arrayfun(filter_val,sqrt(cshift.*cshift + rshift.*rshift));
end

function filter = Gaussian_lowpass_filter(thred, rows, cols)
    or = floor(rows/2);
    oc = floor(cols/2);

    [cidx,ridx] = meshgrid(1:cols,1:rows);

    filter_val = @(x) exp(-x^2/(2*thred*thred));
    cshift = bsxfun(@minus, cidx, oc);
    rshift = bsxfun(@minus, ridx, or);

    filter = arrayfun(filter_val,sqrt(cshift.*cshift + rshift.*rshift));
end