【KMP算法】 【模板】讲解 + 例题 POJ 3461 Oulipo 【求串s1在串s2中出现了多少次，可以交错重复】

【KMP算法】 【模板】讲解 + 例题 POJ 3461 Oulipo 【求串s1在串s2中出现了多少次，可以交错重复】

摘自 KMP算法（1）：如何理解KMP

---

一、背景介绍

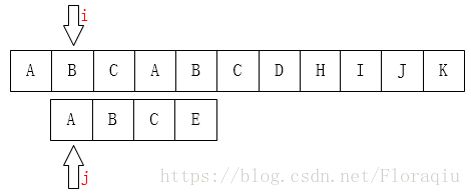
• 给定一个主串（以 S 代替）和模式串（以 P 代替），要求找出 P 在 S 中出现的位置，此即串的模式匹配问题。

• 区分两个概念：真前缀 和 真后缀。

  • “真前缀” ：指除了自身以外，一个字符串的全部头部组合。
  • “真后缀”：指除了自身以外，一个字符串的全部尾部组合。
    

---

二、朴素字符串匹配算法 O(n*m) 模板一

• 思路：从左到右一个个匹配，如果这个过程中有某个字符不匹配，就跳回去，将模式串向右移动一位。

• 初始化
  

• 我们只需要比较i指针指向的字符和j指针指向的字符是否一致。如果一致就都向后移动，如果不一致，如下图：
  

• A和E不相等，那就把i指针移回第1位（假设下标从0开始），j移动到模式串的第0位，然后又重新开始这个步骤：
  

• 复杂度 O（n * m）

---

模板一、 朴素字符串匹配算法 O(n*m) {#1}

/* 字符串下标始于0 */
int NaiveStringSearch(string S, string P)
{
    int i = 0;    //S的下标
    int j = 0;    //P的下标
    int s_len = S.size();
    int p_len = P.size();

    while (i < s_len && j < p_len)
    {
        if (S[i] == P[j])  //若相等，都前进一步
        {
            i++;
            j++;
        }
        else  //不相等
        {
            i = i - j + 1;
            j = 0;
        }
    }

    if (j == p_len)  //匹配成功
        return i - j;

    return -1;
}

---

三：KMP字符串匹配算法 模板二

3.1 算法流程

（1）首先，主串"BBC ABCDAB ABCDABCDABDE"的第一个字符与模式串"ABCDABD"的第一个字符，进行比较。因为B与A不匹配，所以模式串后移一位。

（2）因为B与A又不匹配，模式串再往后移

（3）就这样，直到主串有一个字符，与模式串的第一个字符相同为止。

（4）接着比较主串和模式串的下一个字符，还是相同。

（5）直到主串有一个字符，与模式串对应的字符不相同为止。

（6）这时，最自然的反应是，将模式串整个后移一位，再从头逐个比较。这样做虽然可行，但是效率很差，因为你要把"搜索位置"移到已经比较过的位置，重比一遍。

（7）一个基本事实是，当空格与D不匹配时，你其实是已经知道前面六个字符是"ABCDAB"。KMP算法的想法是，设法利用这个已知信息，不要把"搜索位置"移回已经比较过的位置，而是继续把它向后移，这样就提高了效率。

（8）怎么做到这一点呢？可以针对模式串，设置一个跳转数组int next[]，这个数组是怎么计算出来的，后面再介绍，这里只要会用就可以了。 如何求next数组

i	0	1	2	3	4	5	6	7
模式串	A	B	C	D	A	B	D	‘\0’
next[i]	-1	0	0	0	0	1	2	0

（9）已知空格与D不匹配时，前面六个字符"ABCDAB"是匹配的。根据跳转数组可知，不匹配处D的next值为2，因此接下来从模式串下标为2的位置开始匹配。

（10）因为空格与Ｃ不匹配，C处的next值为0，因此接下来模式串从下标为0处开始匹配。

（11）因为空格与A不匹配，此处next值为-1，表示模式串的第一个字符就不匹配，那么直接往后移一位。

（12）逐位比较，直到发现C与D不匹配。于是，下一步从下标为2的地方开始匹配。

（13）逐位比较，直到模式串的最后一位，发现完全匹配，于是搜索完成。

3.2 next数组是如何求出的 {#3}

3.2.1 next数组求解原理

• next数组的求解基于“真前缀”和“真后缀”，即next[i]等于P[0]…P[i - 1]最长的相同真前后缀的长度（请暂时忽视i等于0时的情况，下面会有解释）。我们依旧以上述的表格为例，为了方便阅读，我复制在下方了。

i	0	1	2	3	4	5	6	7
模式串	A	B	C	D	A	B	D	‘\0’
next[i]	-1	0	0	0	0	1	2	0

• next求解过程

• i = 0，对于模式串的首字符，我们统一为next[0] = -1；

• i = 1，前面的字符串为A，其最长相同真前后缀长度为0，即next[1] = 0；

• i = 2，前面的字符串为AB，其最长相同真前后缀长度为0，即next[2] = 0；

• i = 3，前面的字符串为ABC，其最长相同真前后缀长度为0，即next[3] = 0；

• i = 4，前面的字符串为ABCD，其最长相同真前后缀长度为0，即next[4] = 0；

• i = 5，前面的字符串为ABCDA，其最长相同真前后缀为A，即next[5] = 1；

• i = 6，前面的字符串为ABCDAB，其最长相同真前后缀为AB，即next[6] = 2；

• i = 7，前面的字符串为ABCDABD，其最长相同真前后缀长度为0，即next[7] = 0。

• 那么，为什么根据最长相同真前后缀的长度就可以实现在不匹配情况下的跳转呢？举个代表性的例子：假如i = 6时不匹配，此时我们是知道其位置前的字符串为ABCDAB，仔细观察这个字符串，首尾都有一个AB，既然在i = 6处的D不匹配，我们为何不直接把i = 2处的C拿过来继续比较呢，因为都有一个AB啊，而这个AB就是ABCDAB的最长相同真前后缀，其长度2正好是跳转的下标位置。

• 有的读者可能存在疑问，若在i = 5时匹配失败，按照我讲解的思路，此时应该把i = 1处的字符拿过来继续比较，但是这两个位置的字符是一样的啊，都是B，既然一样，拿过来比较不就是无用功了么？其实不是我讲解的有问题，也不是这个算法有问题，而是这个算法还未优化，关于这个问题在下面会详细说明，不过建议读者不要在这里纠结，跳过这个，下面你自然会恍然大悟。KMP优化

####3.2.2 核心代码

/* P 为模式串，下标从 0 开始 */
void GetNext(string P, int next[])
{
    int p_len = P.size();
    int i = 0;   // P 的下标
    int j = -1;  
    next[0] = -1;

    while (i < p_len)
    {
        if (j == -1 || P[i] == P[j])
        {
            i++;
            j++;
            next[i] = j;
        }
        else
            j = next[j];
    }
}

3.3.3 代码思路解读

（1）i和j的作用是什么？

i和j就像是两个”指针“，一前一后，通过移动它们来找到最长的相同真前后缀。

（2） if…else…语句里做了什么？

假设i和j的位置如上图，由next[i] = j得，也就是对于位置i来说，区段[0, i - 1]的最长相同真前后缀分别是[0, j - 1]和[i - j, i - 1]，即这两区段内容相同。

按照算法流程，if (P[i] == P[j])，则i++; j++; next[i] = j;；若不等，则j = next[j]，见下图：

next[j]代表[0, j - 1]区段中最长相同真前后缀的长度。如图，用左侧两个椭圆来表示这个最长相同真前后缀，即这两个椭圆代表的区段内容相同；同理，右侧也有相同的两个椭圆。所以else语句就是利用第一个椭圆和第四个椭圆内容相同来加快得到[0, i - 1]区段的相同真前后缀的长度。

细心的朋友会问if语句中j == -1存在的意义是何？第一，程序刚运行时，j是被初始为-1，直接进行P[i] == P[j]判断无疑会边界溢出；第二，else语句中j = next[j]，j是不断后退的，若j在后退中被赋值为-1（也就是j = next[0]），在P[i] == P[j]判断也会边界溢出。综上两点，其意义就是为了特殊边界判断。

---

模板二、KMP字符串匹配算法 O（n + m） {#2}

#include
#include
using namespace std;

/* P为模式串，下标从0开始 */
void GetNext(string P, int next[])
{
    int p_len = P.size();
    int i = 0;   //P的下标
    int j = -1;  
    next[0] = -1;

    while (i < p_len)
    {
        if (j == -1 || P[i] == P[j])
        {
            i++;
            j++;
            next[i] = j;
        }
        else
            j = next[j];
    }
}

/* 在S中找到P第一次出现的位置 */
int KMP(string S, string P, int next[])
{
    GetNext(P, next);

    int i = 0;  //S的下标
    int j = 0;  //P的下标
    int s_len = S.size();
    int p_len = P.size();

    while (i < s_len && j < p_len)
    {
        if (j == -1 || S[i] == P[j])  //P的第一个字符不匹配或S[i] == P[j]
        {
            i++;
            j++;
        }
        else
            j = next[j];  //当前字符匹配失败，进行跳转
    }

    if (j == p_len)  //匹配成功
        return i - j;
    
    return -1;
}

int main()
{
    int next[100] = { 0 };

    cout << KMP("bbc abcdab abcdabcdabde", "abcdabd", next) << endl; //15
    
    return 0;
}

---

四、KMP优化 模板三

i	0	1	2	3	4	5	6	7
模式串	A	B	C	D	A	B	D	‘\0’
next[i]	-1	0	0	0	0	1	2	0

以3.2的表格为例（已复制在上方），若在i = 5时匹配失败，按照3.2的代码，此时应该把i = 1处的字符拿过来继续比较，但是这两个位置的字符是一样的，都是B，既然一样，拿过来比较不就是无用功了么？这我在3.2已经解释过，之所以会这样是因为KMP不够完美。那怎么改写代码就可以解决这个问题呢？很简单。

---

模板三、KMP优化 {#4}

/* P为模式串，下标从0开始 */
void GetNextval(string P, int nextval[])
{
    int p_len = P.size();
    int i = 0;   //P的下标
    int j = -1;  
    nextval[0] = -1;

    while (i < p_len)
    {
        if (j == -1 || P[i] == P[j])
        {
            i++;
            j++;
            if (P[i] != P[j])
                nextval[i] = j;
            else
                nextval[i] = nextval[j];  //既然相同就继续往前找其最小的前缀
        }
        else
            j = nextval[j];
    }
}

TIPS：

• KMP算法（未优化版）： next数组表示最长的相同前后缀的长度，我们不仅可以利用next来解决模式串的匹配问题，也可以用来解决类似字符串重复问题等等，这类问题大家可以在各大OJ找到，这里不作过多表述。
• KMP算法（优化版）： 根据代码很容易知道（名称也改为了nextval），优化后的next仅仅表示相同前后缀的长度，但不一定是最长（我个人称之为“最优相同前后缀”）。此时我们利用优化后的next可以在模式串匹配问题中以更快的速度得到我们的答案（相较于未优化版），但是上述所说的字符串重复问题，优化版本则束手无策。
• 所以，该采用哪个版本，取决于你在现实中遇到的实际问题。

---

五、例题 POJ 3461 Oulipo

The French author Georges Perec (1936–1982) once wrote a book, La disparition, without the letter ‘e’. He was a member of the Oulipo group. A quote from the book:

Tout avait Pair normal, mais tout s’affirmait faux. Tout avait Fair normal, d’abord, puis surgissait l’inhumain, l’affolant. Il aurait voulu savoir où s’articulait l’association qui l’unissait au roman : stir son tapis, assaillant à tout instant son imagination, l’intuition d’un tabou, la vision d’un mal obscur, d’un quoi vacant, d’un non-dit : la vision, l’avision d’un oubli commandant tout, où s’abolissait la raison : tout avait l’air normal mais…

Perec would probably have scored high (or rather, low) in the following contest. People are asked to write a perhaps even meaningful text on some subject with as few occurrences of a given “word” as possible. Our task is to provide the jury with a program that counts these occurrences, in order to obtain a ranking of the competitors. These competitors often write very long texts with nonsense meaning; a sequence of 500,000 consecutive 'T’s is not unusual. And they never use spaces.

So we want to quickly find out how often a word, i.e., a given string, occurs in a text. More formally: given the alphabet {‘A’, ‘B’, ‘C’, …, ‘Z’} and two finite strings over that alphabet, a word W and a text T, count the number of occurrences of W in T. All the consecutive characters of W must exactly match consecutive characters of T. Occurrences may overlap.

Input
The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:

One line with the word W, a string over {‘A’, ‘B’, ‘C’, …, ‘Z’}, with 1 ≤ |W| ≤ 10,000 (here |W| denotes the length of the string W).
One line with the text T, a string over {‘A’, ‘B’, ‘C’, …, ‘Z’}, with |W| ≤ |T| ≤ 1,000,000.

Output
For every test case in the input file, the output should contain a single number, on a single line: the number of occurrences of the word W in the text T.

Sample Input
3
BAPC
BAPC
AZA
AZAZAZA
VERDI
AVERDXIVYERDIAN

Sample Output
1
3
0

题意：
求串s1在串s2中出现了多少次，可以交错重复，如样例二，AZAZAZA， AZ( A )Z( A )ZA，共出现了3次。

思路：
KMP，但是每次找到一个后，ans++， 但不要立即跳出来，而是让 j = next[j]。
比如 abcabd，和abcab
1、第一次匹配
|a|b|c|a|b|d|
|–|
| | | | |i | |
|a|b|c|a|b||
| | | | |j | |
2、匹配完后，i,j各向前走一步
|a|b|c|a|b|d|
|–|
| | | | | | i|
|a|b|c|a|b||
| | | | | | j|
3、此时要让j = 0吗？
|a|b|c|a|b|d|| | | |
|–|
| | | | | |i| | | | |
| | | | | |a|b|c|a|b|
| | | | | | j| | | | |
显然这样不划算，因为我已经知道d前面是ab,而ab是可以和abcab匹配的，所以我只需要将d与c比较即可,即让j = next[j]
4、令j = next[j]
|a|b|c|a|b|d|| |
|–|
| | | | | |i| | |
| | | |a|b|c|a|b|
| | | | | | j| | |

5、注意，要是1最后一个位置可以匹配，如样例二中AZAZA 最后一个AZA可以匹配，但是由于这是 i = s_len，已经跳出来了，所以无法进入循环再判断j == p_len，因此，需要最后跳出来时，再判断一下是否有 i == s_len && j == p_len，如果有ans++。

AC代码：

#include 
#include 
#include 
#include 

using namespace std;

const int maxn = 1000005;
int Next[maxn], ans;

void GetNext(string p, int * Next)
{
    int p_len = p.length();
    int i = 0;
    int j = -1;
    Next[0] = -1;
    while(i < p_len)
    {
        if(j == -1 || p[i] == p[j])
        {
            i++;
            j++;
            Next[i] = j;
        }
        else
            j = Next[j];
    }
}

int KMP(string s, string p, int * Next)
{
    GetNext(p, Next);
    int s_len = s.length();
    int p_len = p.length();
    int i = 0;
    int j = 0;
    while(i < s_len)
    {
        if(j == p_len)
        {
            ans++;
            j = Next[j];
        }
        if(j == -1 || s[i] == p[j])
        {
            i++;
            j++;
        }
        else
            j = Next[j];
    }
    if(i == s_len && j == p_len)
        ans++;
    return ans;
}

int main()
{
    int t;
    scanf("%d", &t);
    while(t--)
    {
        string s1, s2;
        cin>>s2>>s1;
        ans = 0;
        KMP(s1, s2, Next);
        printf("%d\n", ans);
    }
    return 0;
}