频繁模式增长算法(FP-growth)
算法提出的背景
尽管有着很多的办法用来提升Apriori算法效率,但是如下的两个问题并没有得到很好的解决:
- 仍会产生大量的候选集,比如 1 0 4 10^4 104个频繁1项集,就需要产生 1 0 7 10^7 107个频繁2项集
- 在产生频繁K项集的过程中,需要重复的扫描数据库,开销很大
FP-growth算法的基本原理
FP-growth算法的提出,就很好的解决了在产生候选项集过程中巨大的开销。
它采用了分治的策略,基本步骤如下:
- 首先,将代表频繁项集的数据库压缩到一棵频繁模式树(FP-Tree)
- 然后把这种压缩后的数据库划分成一组条件数据库,每个数据库关联一个频繁项或“模式段”,并分别挖掘每个条件数据库。
随着被考察模式的“增长”,这种方法可以显著地压缩被搜索的数据集大小。
构造FP树
下面我们首先来看FP-growth算法的第一步,如何根据给定的事务集构造一颗FP树。构造FP树的算法流程如下所示
- 扫描事务数据库 D D D一次。收集频繁项的集合 F F F和它们的支持度。对 F F F按支持度降序排序,结果为频繁项表 L L L。
- 创建 F P FP FP树的根结点,以 n u l l null null标记它。对于 D D D中每个事务 T r a n s Trans Trans,执行如下操作:选择 T r a n s Trans Trans中的频繁项,并按 L L L中的次序排序。设排序后的频繁项表为 [ p ∣ P ] [p | P] [p∣P],其中 p p p 是第一个元素,而 P P P是剩余元素的l列表。调用insert_tree([p | P], T)。该过程执行情况如下:如果 T T T有子女 N N N使得 N . i t e m − n a m e = p . i t e m − n a m e N.item-name = p.item-name N.item−name=p.item−name,则 N N N的计数增加1;否则创建一个新结点 N N N,将其计数设置为1,链接到它的父结点 T T T,并且通过结点链结构将其链接到具有相同 i t e m − n a m e item-name item−name的结点。如果 P P P非空,递归地调用insert_tree(P, N)。
下面我们通过一个具体的例子来看一下FP树的构造过程,假设事务集如下所示
| TID | List of item_IDs |
|---|---|
| T100 | I1, I2, I5 |
| T200 | I2,I4 |
| T300 | I2,I3 |
| T400 | I1,I2,I4 |
| T500 | I1,I3 |
| T600 | I2,I3 |
| T700 | I1,I3 |
| T800 | I1,I2,I3,I5 |
| T900 | I1,I2,I3 |
按照算法的流程,我们首先扫描事务数据库,找到频繁1项集和它们对应的支持度,并降序排列,结果如下
| Item ID | Support count |
|---|---|
| I2 | 7 |
| I1 | 6 |
| I3 | 6 |
| I5 | 2 |
| I4 | 2 |
然后开始构造TP树,首先创建根节点null,然后看第一条事务 T 100 T100 T100={ I 1 , I 2 , I 5 I1,I2,I5 I1,I2,I5},因为此时只有根节点,所以按序创建如下的子树(书上叫节点链结构)

接着处理第二条事务 T 200 T200 T200={ I 2 , I 4 I2,I4 I2,I4},因为已经有了 I 2 I2 I2的节点,只需要创建新的 I 4 I4 I4节点,并将 I 2 I2 I2的计数加1,其余的节点不受影响 。
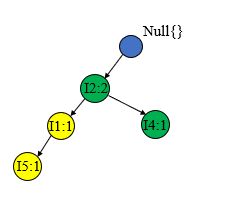
T 300 T300 T300={ I 2 , I 3 I2,I3 I2,I3}和 T 200 T200 T200进行相似的处理,将 I 2 I2 I2计数加1,并创建新的节点 I 3 I3 I3

处理 T 400 T400 T400={ I 1 , I 2 , I 4 I1,I2,I4 I1,I2,I4},方法一样

处理 T 500 T500 T500={ I 1 , I 3 I1,I3 I1,I3}时子树不是以 I 2 I2 I2开始的,所以需要新建一个子树包含 I 1 I1 I1和 I 3 I3 I3

T 600 、 T 700 、 T 800 、 T 900 T600、T700、T800、T900 T600、T700、T800、T900的过程和上面的类似,这里就不一一赘述,直接给出构造过程
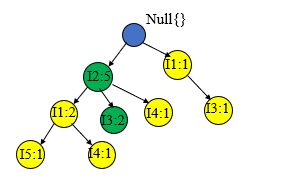



最后我们就可以生成如下的一颗FP树,为了后边挖掘时遍历的方便,创建项头表,使每项通过节点链指向它树中的位置,如下所示。
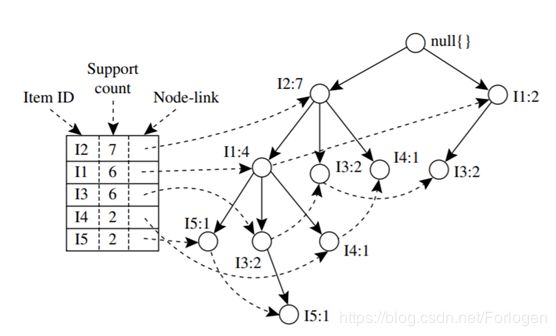
从FP树中挖掘频繁模式
在构造好FP树之后,我们就可以对其进行挖掘。在此之前先阐述两个概念:
-
条件模式基:当选择一后缀,FP树中与该后缀一起出现的前缀路径集。如下所示,当后缀为 I 5 I 5 I5时,它的条件模式基就是{ I 2 , I 1 : 1 I2,I1:1 I2,I1:1}和{ I 2 , I 1 , I 3 : 1 I2,I1,I3:1 I2,I1,I3:1}

-
条件FP树:将得到得条件模式基作为新的事务数据库构造FP树得到的就是条件FP树
在明白了其中涉及的概念后,我们开始从FP树中挖掘频繁模式。
下面先给出从FP树中进行频繁模式挖掘的算法流程,,接下来的挖掘过程就是按照这样的思想一步步进行

为了方便查看,这里再次给出频繁1项集和其支持度的表
| Item ID | Support count |
|---|---|
| I2 | 7 |
| I1 | 6 |
| I3 | 6 |
| I5 | 2 |
| I4 | 2 |
I 5 I5 I5
按照算法的流程,首先看项头表的第一项 I 5 I5 I5(倒序排列), α = n u l l \alpha=null α=null, α 1 = I 5 \alpha_{1}=I 5 α1=I5, β = α ∪ α 1 = I 5 \beta=\alpha ∪ \alpha1=I 5 β=α∪α1=I5, β . s u p = 2 \beta.sup=2 β.sup=2。然后找到 I 5 I5 I5的条件模式基如下所示为{{ I 2 , I 1 : 1 I2,I1:1 I2,I1:1},{ I 2 , I 1 , I 3 : 1 I2,I1,I3:1 I2,I1,I3:1}}

将其作为新的事务集构造FP树如下所示,因为{ I 1 , I 2 , I 3 : 1 I1,I2,I3:1 I1,I2,I3:1}支持度小于2,所以将其删除。得到最后的 T r e e β = Tree_{\beta}= Treeβ= < I 2 : 2 , I 1 : 2 I2:2,I1:2 I2:2,I1:2>,如下所示:

它只有一条路径,包含两个节点,所以只有三种组合方式 β = \beta= β= { I 2 : 2 I2:2 I2:2},{ I 1 : 2 I1:2 I1:2},{ I 2 , I 1 : 2 I2,I1:2 I2,I1:2}, β ∪ α = \beta ∪ \alpha= β∪α={ I 2 , I 5 : 2 I2, I5: 2 I2,I5:2}, { I 1 , I 5 : 2 I1, I5: 2 I1,I5:2}, { I 2 , I 1 , I 5 : 2 I2, I1, I5: 2 I2,I1,I5:2}
故得到的频繁模式为:{ I 2 , I 5 : 2 I2, I5: 2 I2,I5:2}, { I 1 , I 5 : 2 I1, I5: 2 I1,I5:2}, { I 2 , I 1 , I 5 : 2 I2, I1, I5: 2 I2,I1,I5:2}
I 4 I4 I4
然后看 I 4 I4 I4, α = n u l l \alpha=null α=null, α 2 = I 5 \alpha_{2}=I 5 α2=I5, β = α ∪ α 2 = I 5 \beta=\alpha ∪ \alpha_{2}=I 5 β=α∪α2=I5, β . s u p = 2 \beta.sup=2 β.sup=2。然后找到 I 4 I4 I4的条件模式基如下所示为{{ I 2 , I 1 : 1 I2,I1:1 I2,I1:1},{ I 2 : 1 I2:1 I2:1}}

然后同样构造新的FP树 T r e e β = Tree_{\beta}= Treeβ=< I 2 : 2 I2:2 I2:2>,它同样只有一条路径且只包含一个节点,故只有一种组合方式 β = \beta= β={ I 2 , I 4 : 2 I2,I4:2 I2,I4:2},得到新的频繁模式{ I 2 , I 4 : 2 I2,I4:2 I2,I4:2}
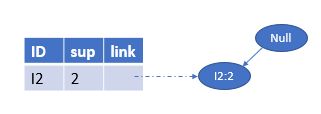
I 3 I3 I3
接着看 α 3 = I 3 \alpha_{3}=I3 α3=I3,同样有 α = n u l l \alpha=null α=null, α 3 = I 3 \alpha_{3}=I 3 α3=I3, β = α ∪ α 3 = I 3 \beta=\alpha ∪ \alpha_{3}=I 3 β=α∪α3=I3, β . s u p = 6 \beta.sup=6 β.sup=6。然后找到 I 3 I3 I3的条件模式基如下所示为{{ I 2 , I 1 : 2 I2,I1:2 I2,I1:2},{ I 2 : 2 I2:2 I2:2},{ I 1 : 2 I1:2 I1:2}}
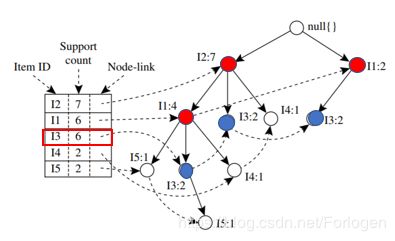
构造的新的FP树 T r e e β = Tree_{\beta}= Treeβ= < I 2 : 4 , I 1 : 2 I2:4,I1:2 I2:4,I1:2>,< I 1 : 2 I1:2 I1:2>,这里和上面的情况不同,这里有两条路径
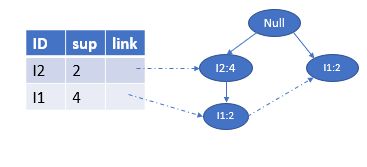
我们需要跳到步骤4,重新继续前面类似的过程如下所示:
先看第一个分支< I 2 : 4 , I 1 : 2 I2:4,I1:2 I2:4,I1:2>, α 1 = I 1 , β = α 1 ∪ α = \alpha_{1}=I1,\beta=\alpha_{1}∪\alpha= α1=I1,β=α1∪α={ I 1 , I 3 I1,I3 I1,I3}, β s u p = 4 \beta_{sup}=4 βsup=4, β \beta β的条件模式基为{ I 2 : 1 I2:1 I2:1},故 T r e e β = Tree_{\beta}= Treeβ=< I 2 : 1 I2:1 I2:1>
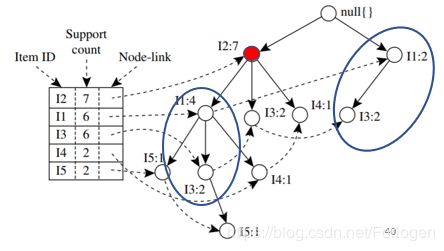
非空,只有一条路径且只包含一个节点,故 β = β ∪ α = \beta=\beta ∪\alpha= β=β∪α={ I 2 , I 1 , I 3 : 2 I2,I1,I3:2 I2,I1,I3:2},,得到频繁模式{ I 2 , I 1 , I 3 : 2 I2,I1,I3:2 I2,I1,I3:2}

看第二个分支< I 1 : 2 I1:2 I1:2>, α 2 = I 2 \alpha_{2}=I2 α2=I2, β = α 2 ∪ α = \beta=\alpha_{2}∪\alpha= β=α2∪α={ I 2 , I 3 I2,I3 I2,I3}, β s u p = 4 \beta_{sup}=4 βsup=4, β \beta β的条件模式基为{ ∅ ∅ ∅},故 T r e e β = Tree_{\beta}= Treeβ={ ∅ ∅ ∅},这里 T r e e β Tree_{\beta} Treeβ为空,所以不再产生新的频繁模式.
故针对 I 3 I3 I3产生的全部频繁模式为{ I 2 , I 1 , I 3 : 2 I2,I1,I3:2 I2,I1,I3:2},{ I 1 , I 3 : 4 I1,I3:4 I1,I3:4},{ I 2 , I 3 : 4 I2,I3:4 I2,I3:4}
之所以有频繁模式{ I 1 , I 3 : 4 I1,I3:4 I1,I3:4},{ I 2 , I 3 : 4 I2,I3:4 I2,I3:4}是因为 I 1 I1 I1和 I 2 I2 I2在最初的FP树中就是 I 3 I3 I3的前缀,所以它们的计数一定大于 I 3 I3 I3,所以它们的组合一定是频繁模式。
I 1 I1 I1
再看 α 4 = \alpha_{4}= α4= I 1 I1 I1, β = α 4 ∪ α = \beta=\alpha_{4}∪\alpha= β=α4∪α={ I 1 I1 I1}, β s u p = 6 \beta_{sup}=6 βsup=6,条件模式基为{ I 2 : 4 I2:4 I2:4}
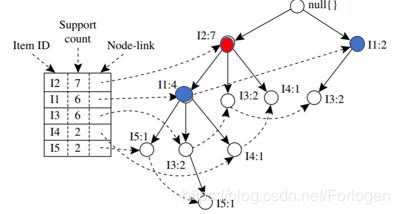
T r e e β = Tree_{\beta}= Treeβ=< I 2 : 4 I2:4 I2:4>只有一条路径,一个节点,一种组合方式,所以 β = \beta= β={ I 2 , I 1 : 4 I2,I1:4 I2,I1:4},得到频繁模式{ I 2 , I 1 : 4 I2,I1:4 I2,I1:4}
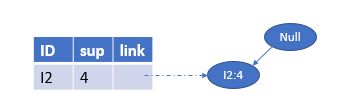
I 2 I2 I2
最后只包含一个节点 I 1 I1 I1的条件模式基为{ I 2 : 4 I2:4 I2:4}, T r e e β = Tree_{\beta}= Treeβ=< I 2 : 4 I2:4 I2:4>,所以得到一个频繁模式{ I 2 : I 1 : 4 I2:I1:4 I2:I1:4}。
所以挖掘原始的事务集构造的FP树得到如上所示的所有频繁模式。
P.S. 最初看这部分内容一下懵住了,么看懂,后来听同学讲才理解了它的整个过程,感谢刘老师的讲述!!
加强强关联规则的提取
前面在Apriori算法中由最小支持度和最小置信度得到的强关联规则具有一定的欺骗性,所以引入了相关性度量来扩充度量框架。
提升度
l i f t ( A , B ) = P ( A ∪ B ) P ( A ) P ( B ) lift(A,B)=\frac{P(A∪B)}{P(A)P(B)} lift(A,B)=P(A)P(B)P(A∪B)
如果值小于1,表示A的出现和B的出现是负相关的;如果值大于1,表示两者是正相关的;如果值等于1,表示A和B是独立的,两者不具有相关性。
全置信度
a l l _ c o n f ( A , B ) = S U P ( A ∪ B ) m a x { s u p ( A ) , s u p ( B ) } = m i n { P ( A ∣ B ) , P ( B ∣ A ) } all\_conf(A,B)=\frac{SUP(A∪B)}{max\{sup(A),sup(B)\}}=min\{P(A|B),P(B|A)\} all_conf(A,B)=max{sup(A),sup(B)}SUP(A∪B)=min{P(A∣B),P(B∣A)}
最大置信度
m a x _ c o n f ( A , B ) = m a x { P ( A ∣ B ) , P ( B ∣ A ) } max\_conf(A,B)=max\{P(A|B),P(B|A)\} max_conf(A,B)=max{P(A∣B),P(B∣A)}
Kulczynski度量
K u l c ( A , B ) = 1 2 ( P ( A ∣ B ) , P ( B ∣ A ) ) Kulc(A,B)=\frac{1}{2}(P(A|B),P(B|A)) Kulc(A,B)=21(P(A∣B),P(B∣A))
余弦
c o s i n e ( A , B ) = P ( A ∪ B ) P ( A ) × P ( B ) = s u p ( A ∪ B ) s u p ( A ) × s u p ( B ) = P ( A ∣ B ) × P ( B ∣ A ) cosine(A,B)=\frac{P(A∪B)}{\sqrt{P(A)\times P(B)}}=\frac{sup(A∪B)}{\sqrt{sup(A)\times sup(B)}}=\sqrt{P(A|B)\times P(B|A)} cosine(A,B)=P(A)×P(B)P(A∪B)=sup(A)×sup(B)sup(A∪B)=P(A∣B)×P(B∣A)
以上的度量方式只受 P ( A ∣ B ) , P ( B ∣ A ) P(A|B),P(B|A) P(A∣B),P(B∣A)的影响,而不受事务总数的影响,每个度量值都0~1,而且值越大,两者的联系越密切。
同时为了评估两个项集之间的不平衡度引入了不平衡比,定义如下:
I R ( A , B ) = ∣ s u p ( A ) − s u p ( B ) ∣ s u p ( A ) + s u p ( B ) − s u p ( A ∪ B ) IR(A,B)=\frac{|sup(A)-sup(B)|}{sup(A)+sup(B)-sup(A∪B)} IR(A,B)=sup(A)+sup(B)−sup(A∪B)∣sup(A)−sup(B)∣
在实际使用中推荐Kulczynski度量和不平衡比一起使用,来提供项集间的模式联系。