最短路径算法 Dijkstra算法与Floyd算法（C++实现）

最短路径算法 Dijkstra算法与Floyd算法（C++实现）

Dijkstra算法又称为单源最短路径，所谓单源是在一个有向图中，从一个顶点出发，求该顶点至所有可到达顶点的最短路径问题。

Floyd算法是解决任意两点间的最短路径的一种算法，可以正确处理有向图或有向图或负权（但不可存在负权回路)的最短路径问题，同时也被用于计算有向图的传递闭包。

如图，求源点1到各顶点的最短路径：

以下是Dijkstra算法C++代码的实现，Dijkstra算法可以理解为Floyd算法少了一层循环，该代码是一个简单的迭代实现，简单易懂。采用向量来存储到各顶点的路径。

#include
#include 
using namespace std;
const int inf = 999999;
const int n = 6;
int L[n][n] = {   0,  7,  9,inf,inf, 14,
                  7,  0, 10, 15,inf,inf,
                  9, 10,  0, 11,inf,  2,
                inf, 15, 11,  0,  6,inf,
                inf,inf,inf,  6,  0,  9,
                14, inf,  2,inf,  9,  0
                 };               //存储图中的路径
int dis[n];        //存储源点到各个顶点的最短路径

vector path[n];
int main()
{
	for (int i = 0; i < n; i++)              //初始化
	{
		dis[i] = L[0][i];
		path[i].push_back(1);
		path[i].push_back(i+1);
	}
	for (int i = 1; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
				//dis[i] = min(dis[i],dis[j] + L[j][i]);
			if (dis[i] > dis[j] + L[j][i])               //求源点到节点的最短路径，利用现有的L矩阵
			{
				dis[i] = dis[j] + L[j][i];		

				path[i].clear();                         //保存并更新路径
				path[i].insert(path[i].end(), path[j].begin(),path[j].end());
				path[i].push_back(i+1);
			}

		}
		for (int m = 0; m < i; m++)              //更新节点最短路径
		{
			for(int j = 0; j < n; j++)
			{
				if (dis[m] > dis[j] + L[j][m])
				{
					dis[m] = dis[j] + L[j][m];
					path[m].clear();                     //保存并更新路径
					path[m].insert(path[m].end(), path[j].begin(), path[j].end());
					path[m].push_back(m + 1);
				}
			}
		}
	}
	vector::iterator ite;
	for (int i = 0; i < n; i++)
	{
		cout << "源点1到"<"<< *ite ;
	}
	    cout << endl;
	}
	
	return 0;
}

运行结果：

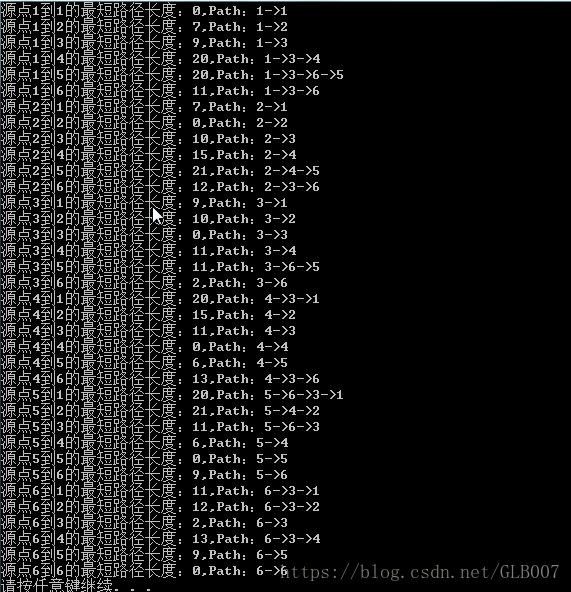
在上面程序的基础上再加一层循环，即可求得任意两个顶点之间的最短路径，即Floyd算法，代码如下：

int main()
{
	for (int i = 0; i < n; i++)              //初始化
	{
		
		for (int j = 0; j < n; j++)
		{
			dis[i][j] = L[i][j];
			path[i][j].push_back(i+1);
		    path[i][j].push_back(j+1);
		}
	}
	for (int k = 0; k < n; k++)
	{
		for (int i = 0; i < n; i++)
	   {
		for (int j = 0; j < n; j++)
		{
				//dis[i] = min(dis[i],dis[j] + L[j][i]);
			if (dis[k][i] > dis[k][j] + L[j][i])               //求源点到节点的最短路径，利用现有的L矩阵
			{
				dis[k][i] = dis[k][j] + L[j][i];

				path[k][i].clear();                         //保存并更新路径
				path[k][i].insert(path[k][i].end(), path[k][j].begin(),path[k][j].end());
				path[k][i].push_back(i+1);
			}
		}
		for (int m = 0; m < i; m++)              //更新节点最短路径
		{
			for(int j = 0; j < n; j++)
			{
				if (dis[k][m] > dis[k][j] + L[j][m])
				{
					dis[k][m] = dis[k][j] + L[j][m];
					path[k][m].clear();                     //保存并更新路径
					path[k][m].insert(path[k][m].end(), path[k][j].begin(), path[k][j].end());
					path[k][m].push_back(m + 1);
				}
			}
		}
	}
	}
	
	vector::iterator ite;
	for (int k = 0; k < n; k++)
	{
		for (int i = 0; i < n; i++)
	{
		cout << "源点"<"<< *ite ;
	}
	    cout << endl;
	}
	}
	return 0;
}

结果如下：